散射是一种非常美丽的自然现象,在自然界中光穿过潮湿或者含有杂质的介质时产生散射,散射的光线进入人眼,让这些介质看起来像拢住了光线一样,也就是所谓的体积光。
在游戏中体积光是很常用的一种光照特效,主要用来表现光线照射到遮蔽物体时,在物体透光部分泄露出的光柱。由于视觉上给人很强的体积感,所以称之为体积光。
体积光特效在现今的中高端游戏中非常常见,优秀的体积光特效在烘托游戏氛围,提高画面质感方面发挥了很大的作用。
作为一种常用特效,体积光的制作方式多种多样,不同游戏对于处理性能,画面要求和渲染质量要求各不相同,也会使用不同的体积光表现方式。
早期游戏中由于机能限制经常使用的是BillBoard贴片和径向模糊这两种方式。
在这里简单介绍一下两种方式,重头戏还是后面最新的基于光线追踪的方式。
BillBoard贴片
BillBoard贴片很容易理解,用PHOTOSHOP生成一个随机的明暗条文,加上遮罩,让它看起来有光条的感觉。
将BillBoard放置在场景中光线会泄露出来的区域,这就是最简单的体积光效果。
做得精细一点的会再加上UV动画,粒子和远景透明的效果。
径向模糊
径向模糊是一种后处理的方法。主要用来表现天空中日月星光散射的效果。
所谓后期处理就是在游戏画面渲染完毕之后,另外加一次渲染,类似于PHOTOSHOP,但处理的对象是每一帧游戏画面,因为速度要求多使用GPU计算。
径向模糊体积光主要流程如下:
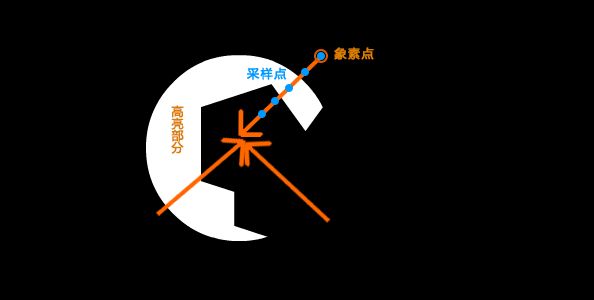
1:渲染出整个画面
2:抽取出画面中高亮的部分
3:对高亮部分进行径向模糊
4:将径向模糊后的高亮层和原图合并
这个流程可以在PS中轻松实现,有兴趣的朋友可以打开PS试一试,我很多时候也会先在PS上试验一些效果,然后再用代码实现。
这里简单介绍一下径向模糊的GPU实现,实现非常简单,就是从原本像素的位置开始,向画面中心移动坐标,每移动一次就采样一次,将所有采样叠加在一起就可以了。
代码如下:
vec2 position = gl_FragCoord.xy / resolution.xy;
Position = (position-0.5)*2.;
position.y =position.y*resolution.y/resolution.x;
vec2 uv = position;
//最后颜色
vec4 color =vec4(vec3(0.),1.);
//采样次数
Const int stepNum =12;
//每次采样衰减
float decay = 0.9;
//采样权重
float weight = 1.;
//坐标移动方向
vec2 direction = normalize(uv);
for(int i=0; i < stepNum ; i++)
{
//移动坐标
uv -= direction/float(stepNum) ;
vec4 sample = texture2D(iChannel0, uv);
sample *=decay ;
color += sample;
weight *= decay;
}
这里可以调整移动步幅,采样的数量,移动的方向,会得到不同的效果。
因为实现简单,消耗小,效果也不错,径向模糊在很多游戏中都有广泛应用,UE4的Atmosphere fog就是用的径向模糊。
另附Webgl径向模糊体积光例子
https://www.shadertoy.com/view/MdG3RD
当然径向模糊的缺点十分明显,如果光源不在画面内,显然径向模糊是没办法执行的。
新的视野
上面两种方式在游戏制作中已经使用了很长时间,但这绝对不表示体积光效果只能做到这个程度,其实还有很大的进步空间。
近期伴随着渲染技术的进步,业界已经开始使用基于光线追踪、阴影贴图等更为精细的渲染技术来实现体积光的效果。
尤其是最近几年,Nvidia、寒霜引擎等几家大厂连续在Siggraph和GDC上发表了多篇关于实时体积光渲染的技术论文。这些算法不论是在模型的精密程度还是计算效率,相较于之前都有了质的飞跃,新一代的体积光已经成为3A游戏的标准配置。
PS:大厂现在做什么都号称是基于物理,实际和真正的物理学、光学比起来精度差得还是千山万水,个人觉得现在实时渲染的技术基本就和古典绘画的光影分析和制作法差不多,非要谈基于物理就有点牵强了。
下面终于要进入正题了,这里会从建模开始一步步深入分析基于光线追踪的体积光算法的各个方面。
我们先从如何描述体积光,也就是为算法建立模型开始。
因为体积光是我们生活中能看到的现象,我们可以从分析自然现象开始,看能不能得到建模的灵感。
首先光自身显然是没有体积的,我们也不可能看见光的形状。那在日常生活中看到的光柱到底是什么,答案很简单其实就空气中的尘埃。
空气中布满大量微小的尘埃,我们看到的光柱就是光线击中尘埃后散射到我们眼睛中的。
这时候有人就说了,那只要把尘埃模拟出来,放到现在的渲染引擎中就万事大吉了。
这当然是最正确的做法,同时却也是最不切实际的做法,因为实时渲染显然不可能在几毫秒内模拟光线在空气中上亿灰尘分子间发生的各种折射、反射、散射。打个比方这就像是让牛顿只用自己的三大定律去计算大海里每个水分子是怎么碰撞的一样。
渲染尤其是实时渲染,最终要的不是所谓的基于物理,而是找到足够近似于真实情况(骗过人眼)的计算方式。
既然不能用蛮力模拟,就要想一些巧妙的办法了,我们先设计一个近似模型,这个模型可以非常简单,只要先表现出一些我们需要的光学性质就行,其他的可以一步一步加上去。
这里我们要思考一下是否需要尘埃数量这么巨大光学特性又很复杂的东西,因为空气中的尘埃非常小,甚至难以看到,不如用一种匀质的物质代替。当然这种物体要和原来渲染引擎的真空不一样,它要能把光折射到观察者眼中,还要符合光传播随着距离增加而衰减的特性。
光线追踪
上面只是这个近似模型的特性描述,真实地写出算法就要考虑怎么看见这种物质,也就是怎么渲染这种物质。
这里我们使用光线追踪的算法框架。
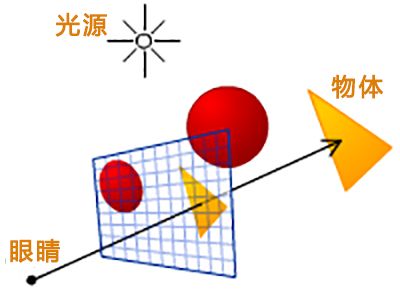
光线追踪简单说就是设置一个虚拟的眼睛,这个眼睛在三维空间里是在屏幕外的一个点。
屏幕上的每个象素渲染的时候,就是从虚拟的眼睛开始做一条射线通过所要渲染的像素,这条射线和屏幕里面的三维空间交汇在哪里(另一种说法射中哪个位置),像素就渲染那个位置的颜色。
注意这里我们不能照搬光线跟踪的定义,要稍微改变一下,因为我们要渲染的这种匀质物体显然不只是表面起作用,而是在射线经过的路径上每个点都会对像素的颜色产生贡献。
我们从起点开始,沿着射线每次推进一点,采样每个点的亮度,所有经过的采样点上的亮度求和就是像素的颜色。
在匀质物理内部每个采样点的亮度值怎么算呢。按照上面模型的规则要符合光传播按距离增加而衰减的特性。这里用一个简单的衰减公式,光的亮度和离光源的距离成平方反比。
就得到了一个公式i = l/d^2。
代码如下:
//ro视线起点,rd是视线方向
vec3 raymarch(vec3 ro, vec3 rd)
{
const int stepNum= 100;
//光源强度
const float lightIntense = 100.;
//推进步幅
float stepSize= 250./stepNum;
vec3 light= vec3(0.0, 0.0, 0.0);
//光源位置
vec3 lightPos = vec3(2.,2.,.5);
float t = 1.0;
vec3 p = vec3(0.0, 0.0, 0.0);
for(int i=0; i
{
vec3 p = ro + t*rd;
//采样点光照亮度
float vLight = lightIntense /dot(p-lightPos,p-lightPos);
light + =vLight;
//继续推进
t+=stepSize;
}
return light;
}
这里要循环那么多次显得很浪费,有没有方法用一个公式算出来呢。
眼尖朋友一定看出来了,这不就是对一个函数求线积分吗。
没错,亮度值是一个空间函数,而光线追踪做的事情其实是求这个函数在视线线段上的线积分。
我们设计的这个简单的模型完全可以用积分的解析解代替光线追踪。
下面是推导过程,当然不考高数,答案可以直接抄。
设函数L(t)=I/r^2
函数x(t)为视线的积分曲线
x(t) = ro +t*rd;
s 为光源
改写L(t)为L(t) = I/|x(t)-s|^2
要求L(t)从0到介质深度d的积分
L(t) = I/dot(p+t*rd-s,p+t*rd-s)
L(t) = I/t^2*dot(rd,rd)+2*dot(p-s,d)t+dot(p-s,p-s)
设dot(p-s,p-s)=c,dot(p-s,d) = b,而且dot(rd,rd)一定等于1
就得到L(t) = I/t^2+2bt+c^2
在裂项L(t) = I/(t^2+2bt+b^2)+(c-b^2)
接着替换u = (t+b),v=(c-b^2)^1/2
积分转换为求 du/u^2+v^2从b到b+d的积分
最后得到I/v*arctan(u/v)从b到b+d
积分解析公式为 I/v*(arctan(b+d/v)-arctan(b/v))
写成代码如下:
float InScatter(vec3 start, vec3 rd, vec3 lightPos, float d)
{
vec3 q = start - lightPos;
float b = dot(rd, q);
float c = dot(q, q);
float iv = 1.0f / sqrt(c - b*b);
float l = iv * (atan( (d + b) * iv) - atan( b*iv ));
return l;
}
现在我们的模型还很简陋,如果单独使用会略显单薄。
这时候就是发挥艺术想象力的时候了,可以结合别的画面元素一起达到漂亮的结果。
下面是两个用例
一个是用作低消耗的光晕,在气球周围的就是球状的体积光
另一个是把体积光框定在圆锥体内部,制造出探照灯的效果。
水下部分的光带是结合了上面提到的贴片制作的。
散射函数
现在再回想一下我们刚才的模型,为什么视线上的所有采样点的亮度之和能用来表示光线在介质中散射的效果呢。
其实我们在假设每个点上都有个尘埃,光照射到尘埃上时,会把所有光准确都反射到我们的眼睛里。
如果研究得更精细一点就会发现,尘埃并没有自动跟踪系统,是不可能正好把所有光都反射到眼睛里的。
光的散射应该是向四面八方的,在一个以尘埃为球心的球体中几乎所有方向都有可能反射到光线,而且每个方向散射出去的光线亮度应该是不一样的,而这些散射出去的光线亮度总合应该和射到尘埃上的那束光线亮度一样,也就是能量守恒。
这种散射可以用一个公式来表示,称为HG公式。
这个公式就是输入指定方向和光线入射方向夹角的cos值,求出指定方向散射光线的亮度。
我们要计算的是朝着眼睛方向的散射光线亮度。
代码如下:
float cosTheta = dot(lightDr,-rd);
float result = (1/4*3.14)* ((1 - g^2)/ (pow(1 + g^2 -2*g* cosTheta, 1.5)));
公式中的g值代表了介质散射性质,图中显示了不同g值对散射的影响。
透光比
模型另一个要改进的部分是光线透光比例。
透光现象就是说光在介质内内传播,会被吸收一部分,剩下的部分才能透过介质达到观察者眼中。
这里要用一个物理法则Beer–Lambert法则。这个法则描述的是入射光强度和透光强度的比值。
这个公式可以简单的写成,Out = In*exp(-c*d)。
c是物质密度,d是距离。
透光强度随着介质的密度光传播的距离的增加成指数下降。
阴影
体积光还有一个重要的元素,阴影,就是它的加入让体积光产生了各种形状。
没有阴影的体积光其实就是雾。
阴影的计算在实时渲染中是比较复杂的,要展开讲内容很多,这里只介绍一下简单的原理。
按照我们的模型图来看,每一次采样的时候如果采样点被阴影遮住了,就直接认为采样结果为0。
所以需要知道一个关键信息,就是采样点是否被光照到。
计算过程简单描述起来就是,连接采样点和光源点作一条线段,然后检测场景中这条线段有没有和别的可见物体相交。如果有交点就判定该采样点被阴影遮挡,不记入采样数据,反之正常计算。
线段和几何形状的求交公式翻一下图形学的课本都能很快找到,这里就不再赘述了。
最终公式
将上面三项加入我们的模型后,来重新审视一下我们的模型。
在每个采样点上都需要计算四个参数,来自光源的光照亮度L,采样点到眼睛的透光率T,光线在视线方向上的散射值P,阴影值V。
如果是非均匀介质,比如有噪音的雾,还要计算采样点位置的介质密度D。
散射S= L*T*V*P*D
这就是最终的散射公式。
具体代码可以参看这个例子
从算法到现实
在实际游戏开发的时候,还有很多算法优化的部分。
一、使用3d纹理保存光照和阴影信息
因为游戏渲染的时候同样需要计算阴影和光照,没必要为了渲染体积光重新计算一遍。论文[1]提出的算法是在游戏渲染的同时将光照和阴影保存在一个3d纹理中,之后计算体积光只要对3d纹理中的信息采样就行了。3d纹理的保存方式也有很多种,UE4使用了一种层级式样的3d纹理,因为同时保存了空间层级数据,在3d索引时更快。
二、使用随即采样减少采样次数
今年的独立游戏公司DeadPlay使用了随即采样的方法,很大程度上减少了光线追踪采样的次数,每个象素只采样了3次,使得高端的游戏特效在手机端也可以顺畅运行。
三、添加噪点和抗锯齿算法柔滑画面
随机采样可以结合TemporalAA算法平滑画面,每一帧的随机采样生成的随机场和TemporalAA每帧的ID关联,这样把采样分散到时间维度上,平滑后同样能达到较高的精度。
参考文献
[1]Volumetric Fog SIGGRAPH 2014 - Advances in Real-Time Rendering
[2]Fast, Flexible, Physically-Based Volumetric Light Scattering - NVIDIA Developer
[3]Physically-based & Unified Volumetric Rendering in Frostbite
[4]Low Complexity, High Fidelity - INSIDE Rendering - GDC
[5]Fogshop: Real-Time Design and Rendering of. Inhomogeneous, Single-Scattering Media.