Tree 小结

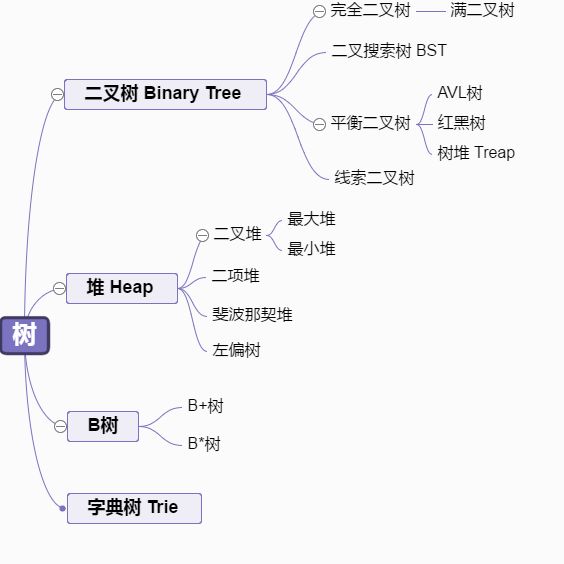
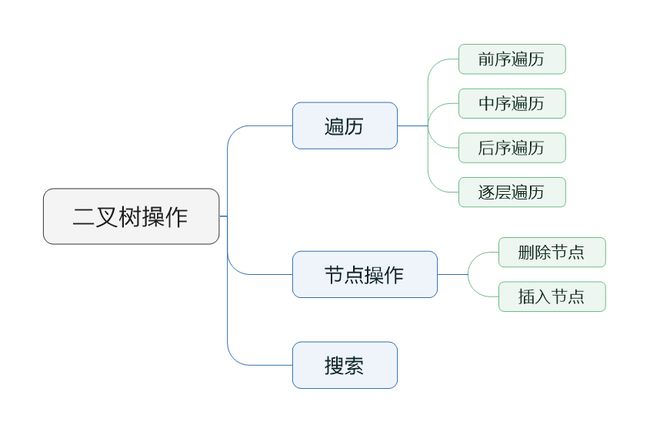
以下是数据结构部分的主要知识点的思维导图

tree_introduce.png

在这段时间基本上刷的都是跟二叉树有关的题目，所以下面主要针对二叉树部分进行总结。
　　二叉树的各种操作基本上离不开基本的几个点，遍历、搜索、节点插入和删除。利用这几个操作互相结合就能解决大部分问题，当然前提是先理解它们的意义和熟悉操作代码的编写。下面分别对这些操作进行代码的实现与分析。

二叉树操作.png

假设树的结构体实现如下：

 Definition for a binary tree node.
  struct TreeNode {
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode(int x) : val(x), left(NULL), right(NULL) {}
  };

遍历（前序、中序、后序）

以中序遍历为例(其他两种情况大同小异)，假设现在需要对一个根节点为root(不为空)的树进行遍历将节点的值按顺序放到vector中，这种情况下同常有递归和非递归两种实现方式，实现代码如下：

递归实现

class Solution {
public:
    vector traverse(TreeNode* root, vector& vec) {
         traverse(root->left);
         vec.push_back(root->val);
         traverse(root->right);
         return vec;
   }
};

使用栈实现h

1.遍历后树会发生变化的实现方式

class Solution {
public:
    vector traverse(TreeNode* root, vector& vec) {
           stack s;
           s.push(root);
           while(!s.empty()){
             TreeNode* node = s.top();
              if(node ->left){
                  s.push(node ->left);
                  node ->left = NULL;//防止重复遍历
              }else{
                  s.pop();
                  vec->push(node->val);
                   if(node->right){
                     s.push(node->right);
                   }   
              } 
          }
       }
       return vec;
   }
};

2.遍历后原树不会发生变化(使用unordered_map)

class Solution {
public:
    vector traverse(TreeNode* root, vector& vec) {
           unordered_map map;
           stack s;
           s.push(root);
           while(!s.empty()){
             TreeNode* node = s.top();
              if(node ->left && !map[node]){
                  s.push(node ->left);
                  map[node->left] = true;
              }else{
                  s.pop();
                  vec->push(node->val);
                   if(node->right){
                     s.push(node->right);
                   }   
              } 
          }
       }
       return vec;
   }
};

3.遍历后原树不会发生变化(不使用unordered_map)

class Solution {
public:
    vector inorderTraversal(TreeNode *root) {
        vector vector;
        stack stack;
        TreeNode *pCurrent = root;

        while(!stack.empty() || pCurrent)
        {
            if(pCurrent)
            {
                //同一根节点下的左右节点，左节点比右节点先出栈（即左节点后进栈,其实最后所有进栈的节点都可以视左一个树中的中间节点。）
                stack.push(pCurrent);
                pCurrent = pCurrent->left;//若左节点为空则，该节点可以等同为中间节点，相对于其右节点先出栈（后进栈）
            }//节点为空就出栈
            else
            {//当左子节点或右子节点没有左子节点时 改节点出栈
                TreeNode *pNode = stack.top();
                vector.push_back(pNode->val);
                stack.pop();
                pCurrent = pNode->right;
            }
        }
        return vector;
    }
};

由于篇幅所限前序遍历和后序遍历的代码就不贴了，可去这个地方查看：
https://github.com/kid1943/leetcode/tree/master/tree/Binary%20Tree%20Preorder%20Traversal

https://github.com/kid1943/leetcode/tree/master/tree/Binary%20Tree%20Postorder%20Traversal

逐层遍历

自上而下

class Solution {
public:
    vector traverse(TreeNode* root) {
        queue q;
        queue level;
        
        q.push(root);
        level.push(0);
        
        vector vec;
        int m = -1;
        int result;
        while(q.size()){
          TreeNode* sr = q.front();
          result = sr->val;
          int l = level.front();
          level.pop();
          q.pop();  
          
          if(sr->left){
              q.push(sr->left);
              level.push(l+1);
          }
          
          if(sr->right){
              q.push(sr->right);
              level.push(l+1);
          }
        }
        return level;
    }
};

节点的删除

要删除二叉搜索树中的某个节点p需要考虑三种情况：
1）p有两颗非空子树
2）p是树叶
3）p是只有一颗非空子树

删除p节点的思路
1）要删除的节点p具有两颗非空子树。先将该节点的元素替换为它的左子树的最大元素或右子树的最小元素。
2）要删除的节点是叶子节点。处理的方法是释放该节点空间，若是根节点，则令根为NULL。
3 ) 要删除的节点p只有一颗子树。如果p没有节点(即p是根节点)，则p的唯一子树的根节点成为新的搜索树的根节点。如果p有父节点pp，则修改pp的指针域，使得它指向p的唯一孩子，然后释放节点p。

以下是我实现的代码

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        root = deleteNodeitem(root, key);
        return root; 
    }

    TreeNode* deleteNodeitem(TreeNode* root, int key){
        TreeNode* p = root;//the keynode to delete
        TreeNode* pp = root;//parentNode of the keynode
        TreeNode* s;//the node to replace the keynode
        TreeNode* ps;//parent node of replacenode

        //findout the keynode p and its parant node pp
        while((p != NULL)&&(p->val != key)){
            pp = p;
            if(key > p->val){
               p = p->right;    
            }else if(key < p->val){
               p = p->left;
            }
        }
        //can not find the keynode
        if(p == NULL){
            return root;
         }

        //state1 node p have 2 nonull childnode
        if((p->left!=NULL)&&(p->right!=NULL)){
            //find the biggest node in the right tree
            s = p->right;
            ps = p;
            while(s->left != NULL){
                ps = s;
                s = s->left;
            }
           //初始化一个要替换删除节点的节点
           TreeNode q = {s->val};
           q.left = p->left; 
           q.right = p->right;
           //将删除节点指向新构造出来的节点q
           if(pp->left == p){
                pp->left = &q;
            }else if(pp->right == p){
                pp->right = &q;
            }else if(p == root){//要删除的节点就是根节点
                pp->val = q.val;
            }

            //make the s node to delete 找出节点s所对应的父节点
            if(ps != p){
                pp = ps;
            }else if((p == ps)&&(p!=root)){//当s的父节点即为p节点时
                pp = &q;
            }
            p = s;//it must one left child of p if p has child
        }

        //statue2 node p have at most one nonull childnode
       //在只有一个非空子树的情况下，只需要将删除子树的非空子树将其替换就可以了
        TreeNode* pc = p;//the child of p , if it has. 
        if(p->left != NULL){
            pc = p->left;
        }else if(p->right != NULL){
            pc = p->right;
        }else{
            pc = NULL;//p has no child
        }

        if(pp->left == p){
            pp->left = pc;
        }else if(pp->right == p){
            pp->right = pc;
        }else{
            root = pc;//根节点就是需要删除的节点
        }
        return root;
    }
};

利用递归

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (!root) return nullptr;
        if (root->val == key) {
            if (!root->right) {
                TreeNode* left = root->left;
                delete root;
                return left;
            }
            else {
                TreeNode* right = root->right;
                //找出右子树的最小节点  
                while (right->left)
                    right = right->left;
                swap(root->val, right->val);    
            }
        }
       //利用递归找出左右子树中要删除的节点，
       //并利用该节点的右子树中的左子树的最小节点替换掉要被删除的节点
        root->left = deleteNode(root->left, key);
        root->right = deleteNode(root->right, key);
        return root;
    }
};

题目思路整理

Find Bottom Left Tree Value 逐层遍历
Find Largest Value in Each Tree Row 逐层遍历或前序遍历
Find Largest Value in Each Tree Row 利用中序遍历可以得到由小到大的集合
Maximum Depth of Binary Tree 后序遍历或逐层遍历
Most Frequent Subtree Sum 中序遍历，计算每个节点的值及其左右子树的值之和
Invert Binary Tree 后序遍历
Binary Tree Tilt 后序遍历求和
Sum of Left Leaves 前序遍历，找出左子叶
Same Tree 后序或前序遍历节点进行比较
Binary Tree Inorder Traversal 中序遍历的实现

未完待续

Tree 小结

遍历 （前序、中序、后序）

逐层遍历

节点的删除

题目思路整理

你可能感兴趣的:(Tree 小结)

遍历（前序、中序、后序）