垒骰子
赌圣atm晚年迷恋上了垒骰子,就是把骰子一个垒在另一个上边,不能歪歪扭扭,要垒成方柱体。
经过长期观察,atm 发现了稳定骰子的奥秘:有些数字的面贴着会互相排斥!
我们先来规范一下骰子:1 的对面是 4,2 的对面是 5,3 的对面是 6。
假设有 m 组互斥现象,每组中的那两个数字的面紧贴在一起,骰子就不能稳定的垒起来。
atm想计算一下有多少种不同的可能的垒骰子方式。
两种垒骰子方式相同,当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多,请输出模 10^9 + 7 的结果。
不要小看了 atm 的骰子数量哦~
「输入格式」
第一行两个整数 n m
n表示骰子数目
接下来 m 行,每行两个整数 a b ,表示 a 和 b 数字不能紧贴在一起。
「输出格式」
一行一个数,表示答案模 10^9 + 7 的结果。
「样例输入」
2 1
1 2
「样例输出」
544
「数据范围」
对于 30% 的数据:n <= 5
对于 60% 的数据:n <= 100
对于 100% 的数据:0 < n <= 10^9, m <= 36
解题思路
首先,这题有很多的解题方式,但这里主要使用矩阵快速幂来解决,如果对矩阵快速幂不是很熟悉的玩家,呸,读者。。请看一下前面的两篇文章矩阵快速幂入门和矩阵快速幂进阶
看到这道题目,第一感觉是,这题怎么能用矩阵快速幂做?递推式都没给,怎么求转移矩阵呢?
首先我们理解一下题目
我们先看一下只有一组互斥现象1-2,且n=1、n=2、n=3的情况,也就是以下三组测试数据
#测试数据一 #测试数据二 #测试数据三
1 1 2 1 3 1
1 2 1 2 1 2
- 第一个测试数据(先不考虑侧面的旋转)
| 情况 | 点1朝上 | 点2朝上 | 点3朝上 | 点4朝上 | 点5朝上 | 点6朝上 |
|---|---|---|---|---|---|---|
| 第一层 | 1 | 1 | 1 | 1 | 1 | 1 |
总数 = (1+1+1+1+1+1) × 41 = 24 (侧面每种情况都能进行4种旋转)
- 第二个测试数据(先不考虑侧面的旋转)
| 情况 | 点1朝上 | 点2朝上 | 点3朝上 | 点4朝上 | 点5朝上 | 点6朝上 |
|---|---|---|---|---|---|---|
| 第一层 | 1 | 1 | 1 | 1 | 1 | 1 |
| 第二层 | 6 | 6 | 6 | 5 | 5 | 6 |
总数 = (6+6+6+5+5+6) × 42 = 544 (侧面每种情况都能进行4种旋转)
- 第三个测试数据(先不考虑侧面的旋转)
| 情况 | 点1朝上 | 点2朝上 | 点3朝上 | 点4朝上 | 点5朝上 | 点6朝上 |
|---|---|---|---|---|---|---|
| 第一层 | 1 | 1 | 1 | 1 | 1 | 1 |
| 第二层 | 6 | 6 | 6 | 5 | 5 | 6 |
| 第三层 | 34 | 34 | 34 | 28 | 28 | 34 |
首先,解释一下上述表格的意思,比如第二层,点1朝上对应是6意思是:当只有两层的时候,第二层(最上面的一层)顶面的点数是1的情况,一共有6种。
为什么是6?点1朝上,也就说明点4朝下,因为没有和4冲突的,所以第一层怎么放都可以,一共6种(也就是第一层的6种情况相加)
那第二层,点4朝上的时候为什么对应的是5呢?点4朝上,也就说明点1朝下,因为1-2是互斥现象,所以第一层中点2朝上的情况就不能加上了,所以一共5种。
现在到了第三层。第三层,点1朝上的情况一共有34种(再重复一遍,第三层点1朝上的情况,是指最上面那个骰子点1朝上,然后下面两个骰子可以存在的所有情况)。为什么是34?因为点1朝上,也就是说点4朝下,和任何数字都不冲突,所以是第二层的所有情况相加(是不是感觉进DP的坑了)
然后看下第三层,点4朝上的情况,点4朝上也就说明点1朝下,因为1-2是互斥现象,所以第三层中点4朝上的情况 = 第二层中点1+点3+点4+点5+点6朝上的情况的总和
这真的不是DP吗?和矩阵快速幂有啥关系
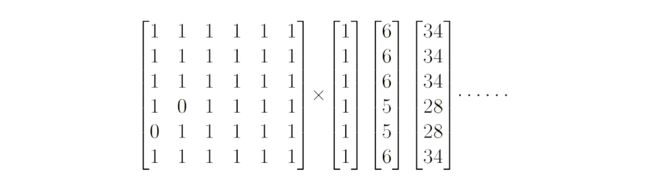
乘号右边,从上到下分别是
点1朝上、
点2朝上……的情况,从左到右分别是第一层、第二层、第三层的情况。
那是怎么得到这个转移矩阵的呢??再回上去看下,刚才递推出来的各层的情况,除了和DP类似,是不是也和一个递推公式很类似呢?
dp[i][j] = ∑ dp[i-1][j] (1<=j<=6)
其中dp[i][j]表示第i层,点j朝上的情况
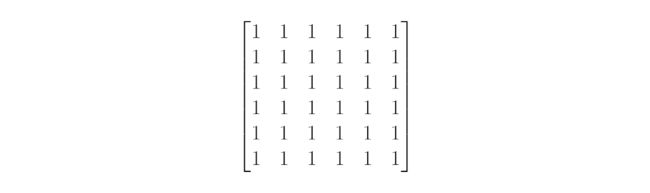
如果仅仅是单纯的前一层的各个情况相加,我们的转移矩阵可以是这样的
但是我们还有一步,需要把互斥现象组去掉。那怎么去呢?把该点置0?对!!比如互斥组1-2,当点4朝上时,点1就朝下,这时,子层不能加上点2朝上的情况,所以需要把A[4][2]置0。当点5朝上时,点2就朝下,子层不能加上点1朝上的情况,所以需要把A[5][1]置0
这里的A[5][1]表示第5行第1列,在真正意义上的数组计算时,使用的是A[4][0]
for(int i=0; i>a>>b;
temp[dp[a]-1][b-1] = temp[dp[b]-1][a-1] = 0;
}
上述代码中,比如输入互斥现象1 3。因为点1对面是点5。所以当点5朝上时,点1朝下,子层不能出现点3朝上的情况。同理点3对面是点6,所以当点6朝上时,点3朝下,子层中不能出现点1朝上的情况。因为数组从0开始,所以有temp[dp[a]-1][b-1] = temp[dp[b]-1][a-1] = 0;
不过最后还需要注意一点!4n不要忘了,因为侧面的情况开始就没考虑。但是每一层的侧面有4种情况,所以第n层的总情况只要将上述结果乘以4n就可以了。
完整代码
#include
#include
using namespace std;
const long long int N = 1000000007;
void Matrix(long long int (&a)[6][6],long long int b[6][6]){
long long int tmp[6][6] = {0};
for(int i = 0; i < 6; ++i)
for(int j = 0; j < 6; ++j)
for(int k = 0; k < 6; ++k)
tmp[i][j] = (tmp[i][j] + a[i][k] * b[k][j]) % N;
for(int i = 0; i < 6; ++i)
for(int j = 0; j < 6; ++j)
a[i][j] = tmp[i][j];
}
int main(int argc, const char * argv[]) {
long long int n,m,a,b,sum = 0,p = 4,temp[6][6],cot[6][6] = {0},dp[7] = {0,4,5,6,1,2,3};
cot[0][0] = cot[1][1] = cot[2][2] = cot[3][3] = cot[4][4] = cot[5][5] = 1;
fill(temp[0],temp[0]+36,1); //初始化为1
cin>>n>>m;
for(int i=0; i>a>>b;
temp[dp[a]-1][b-1] = temp[dp[b]-1][a-1] = 0; //互斥位置0
}
m = n - 1;
while(m){ //计算矩阵快速幂
if(m & 1) Matrix(cot,temp);
Matrix(temp,temp);
m /= 2;
}
for(int i=0; i<6; i++)
for(int j=0; j<6; j++)
sum = (sum + cot[i][j])%N; //结果集之和
while(n){ //同快速幂求解4^n
if(n&1) sum = (sum*p)%N; //注意一开始是sum开始乘的
p = (p*p)%N;
n /= 2;
}
cout< 由于找不到提交代码的地方,所以这不算是已经AC的代码,不过试了一些数据,和标程的输出都一样