贝塞尔曲线的神秘之处就是能实现非常酷炫的动画效果,,对此还需先了解它的原理.先来看下贝塞尔曲线是什么样子的。
贝塞尔曲线分为几种阶段的曲线,一般我们常用到的是二阶,三阶。四阶也有。更高阶的比较少见到,而且android提供给我们的方法也就到三阶的方法。四阶以上需要自己写算法去计算。他们的实现都有分别不同的公式实现,先上图。
一阶是一条直线,这没什么好说的。
公式:
二阶贝塞尔曲线:
三阶贝塞尔曲线:
四阶贝塞尔曲线:
以上就是常见的贝塞尔曲线的曲线样子。
虽然有这些公式,但是具体的绘制原理是什么呢。
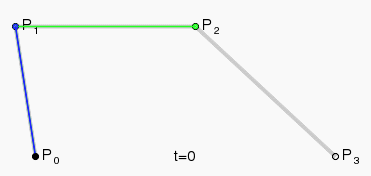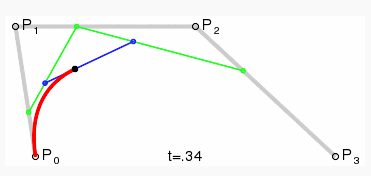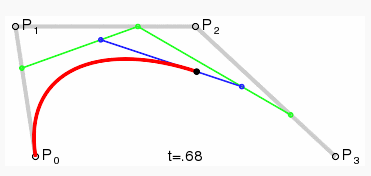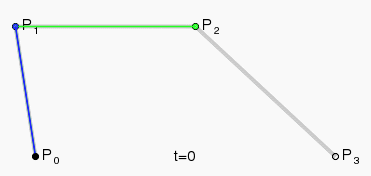
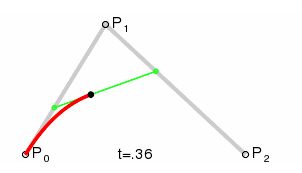
这些公式的里有一个t的参数。这个t表示的是时间值。取值为0到1。先从简单的二阶曲线讲起吧。
可以看到,po是起点,p2是终点,但是这个p1点就起到了关键作用。p1可以说成是控制点。我们假设知道三个点的坐标已知。在某个t时刻,将这个t值代入到公式里。就可以算出在这个当前时刻的点坐标。所以这个t值,如果从0到1全部算出得到所有的点坐标,连起来也就是我们所看到的二阶曲线。那图中的绿色线的两个点又表示的是什么意思呢。
这个t值在这里也可以理解为比例值。从p0到p1这条线的36%的位置标记点。从p1到p2这条线的36%的位置标记点。这个两个点连起来的线,再在它的36%的位置标记点。这个最终算点的位置也是就是t位置0.36时刻的坐标点。所以同样在3阶,4阶,以及n阶的曲线,都是按照这样的原理去绘制点。
原理都懂了。先看看代码是如何实现的。我们先自定义一个类继承View,实现构造方法,onDraw方法。需要画笔和画线的类。
"public class Test3Line extends View {
public Test3Line(Context context) {
super(context);
initView();
}
public Test3Line(Context context, AttributeSet attrs) {
super(context, attrs);
initView();
}
public Test3Line(Context context, AttributeSet attrs, int defStyleAttr) {
super(context, attrs, defStyleAttr);
initView();
}
@RequiresApi(api = Build.VERSION_CODES.LOLLIPOP)
public Test3Line(Context context, AttributeSet attrs, int defStyleAttr, int defStyleRes) {
super(context, attrs, defStyleAttr, defStyleRes);
initView();
}
private final Paint mPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
private final Path mPath = new Path();
private void initView(){
Paint paint = mPaint;
//抗锯齿
paint.setAntiAlias(true);
//抗抖动
paint.setDither(true);
//线的粗细
paint.setStyle(Paint.Style.STROKE);
paint.setStrokeWidth(5);
//一阶
Path path = mPath;
path.moveTo(100,100);
path.lineTo(400,400);
//二阶的方法
path.quadTo(600,100,800,400);//前两个参数是控制点xy的高度,后面两个是最终点的位置。
//相对的实现 灵活。随机应变。增加多少。
// path.rQuadTo(200,-300,400,0);
path.moveTo(400,800);
// path.rQuadTo(200,-300,400,0);
//三阶的方法。
// path.cubicTo(500,600,700,1200,800,800);
path.rCubicTo(100,-200,300,400,400,0);
}
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
canvas.drawPath(mPath,mPaint);
}
}
上面二阶的有了quadTo方法,为啥还有个rQuadTo方法,这个方法就像是相对布局一样。相对于前一个坐标点,加入你想要的增加的值就能算出quadTo方法一样的效果。
同样,三阶的rCubicTo()方法也是同样的道理。
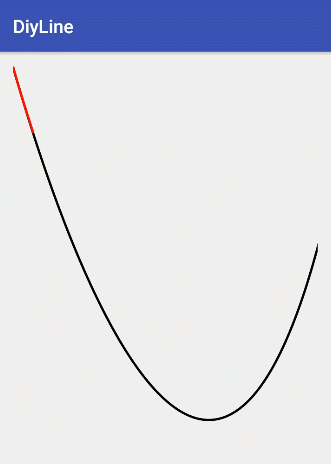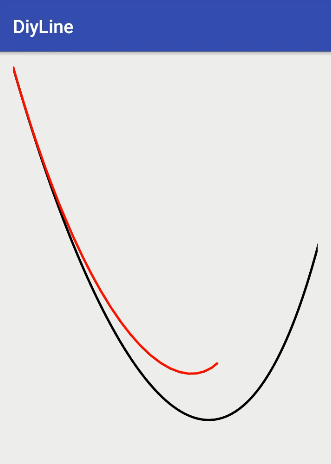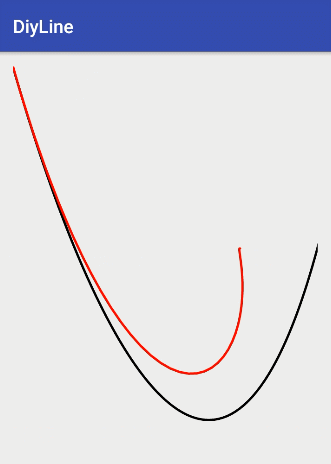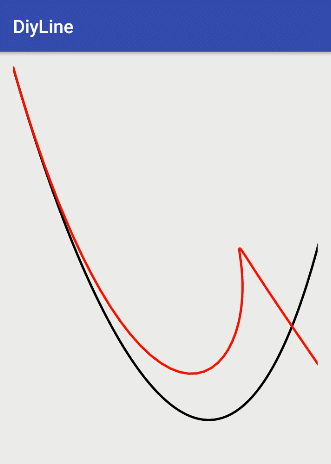
最后绘制出的图
四阶以及N阶之后,android就没有提供相应的方法了。下面就给出相应的算法吧
public class BezierView extends View {
public BezierView(Context context) {
super(context);
init();
}
public BezierView(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
public BezierView(Context context, AttributeSet attrs, int defStyleAttr) {
super(context, attrs, defStyleAttr);
init();
}
private Path mBezirer = new Path();
private Path mSrcBezirer = new Path();
private Paint mPaint = new Paint(Paint.ANTI_ALIAS_FLAG);
@RequiresApi(api = Build.VERSION_CODES.LOLLIPOP)
public BezierView(Context context, AttributeSet attrs, int defStyleAttr, int defStyleRes) {
super(context, attrs, defStyleAttr, defStyleRes);
init();
}
private void init(){
//初始化画笔
Paint paint = mPaint;
paint.setAntiAlias(true);
//抗抖动
paint.setDither(true);
paint.setStyle(Paint.Style.STROKE);
paint.setStrokeWidth(5);
//初始化贝塞尔曲线4阶
//initBezier();
//初始化原线
mSrcBezirer.cubicTo(200,700,500,1200,700,200);
new Thread(){//开启线程,延迟绘制出曲线
@Override
public void run(){
initBezier();
}
}.start();
}
/**
* 初始化贝塞尔曲线
*/
private void initBezier(){
//6阶曲线
//数组中,第一个和最后一个为起始点的x或者y坐标,中间的就是控制点的x或y坐标
float[] xPoints= new float[]{0,200,500,700,400,300,900};//5个控制点的x坐标
float[] yPoints = new float[]{0,700,1200,200,400,100,1000};//5个控制点的y坐标
//float progress = 0.2f;// ...
//calculateBezier(progress,xPoints);
Path path = mBezirer;
int fps = 1000;//刷新频率
for(int i = 0;i <= fps;i++){
//进度
float progress = i/(float)fps;// ...
float x = calculateBezier(progress,xPoints);
float y = calculateBezier(progress,yPoints);
//使用链接的方式,当xy变动足够小的情况下,就是平滑曲线.
path.lineTo(x,y);
//刷新界面
postInvalidate();
try {
Thread.sleep(50);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
}
/**
* 计算某时刻的贝塞尔所处的值 (x或y)
* @param t 时间(0~1)
* @param values 贝塞尔点集合 (x或y)
* @return 当前t时刻 的贝塞尔所处点
*/
private float calculateBezier(float t,float... values){
//循环计算
//采用双层for循环
final int len = values.length;
for(int i = len-1;i>0;i--){
//外层
for(int j = 0;j6阶曲线最终效果