PCA原理简介
为什么要用PCA?
维基百科介绍:主成分分析(英语:Principal components analysis,PCA)是一种分析、简化数据集的技术。主成分分析经常用于减少数据集的维数,同时保持数据集中的对方差贡献最大的特征。
说了和没说一样……我们还是通过一个简单的案例引出PCA的作用吧。
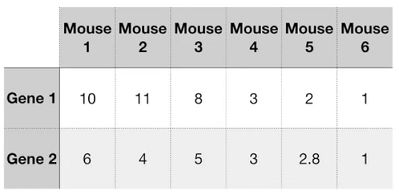
如果我们在6个小鼠样本中检测一个基因Gene1的表达
我们很容易看出来,基因Gene1在小鼠1-3中表达比较相似,而在小鼠4-6中表达比较相似
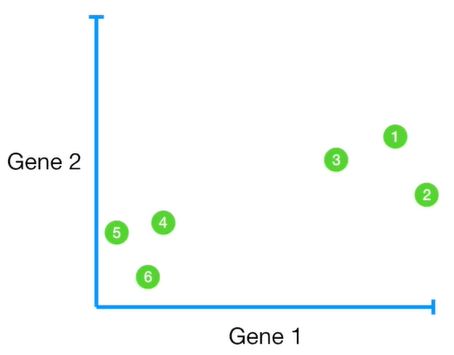
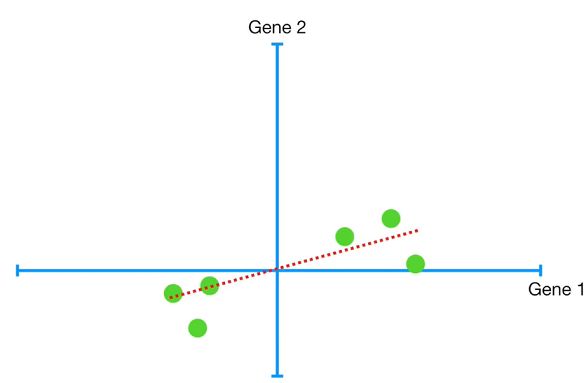
如果同时检测两个基因
我们可以将不同小鼠样本标记在二维坐标轴中,并且看出小鼠1-3的整体表达比较相似,而小鼠4-6的整体表达比较相似
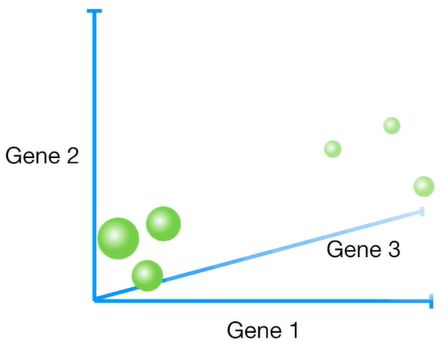
将基因数目扩增到3个时候,我们依然可以通过三维坐标轴标记出不同样本的分布
但是如果将基因数目增加到4个或4个以上时候,很难继续增加坐标轴的维度来绘图(思维空间已经超出一般人的认知了)。
所以我们可以通过PCA的降维方法来处理这种4维或者多维数据,将其绘制为二维图像来比较不同样本之间的关系。
PCA原理
PCA是如果进行降维的呢?
PC1计算原理
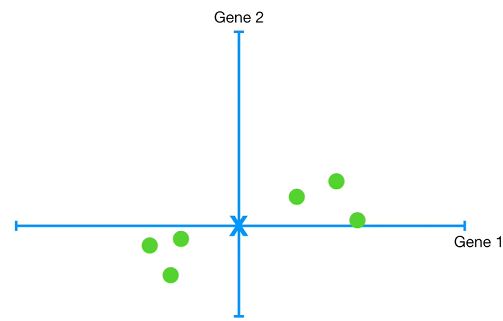
首先我们只检测6个不同小鼠的2个基因,那么我们可以分别计算出所有小鼠Gene1和Gene2的平均值(红色叉号)。根据这些均值,可以获得所有数据的中心(蓝色叉号)。
然后我们将数据整体移动,数据的中心于原点重合。虽然所有的数据点都移动了,但是每个数据点的相对距离没有改变,只是数据的中心变为原点(0,0)。
接下来,我们会绘制一条通过原点的直线。这条直线可以360°旋转,直至同数据匹配最佳。
那么如何判断最佳匹配呢?这个标准是——
PCA将所有的数据点投射到这条直线上,并且计算这些数据点投射到直线上的距离(使这些距离最小)和投射点到原点的距离(使这些距离最大)
如何理解这两个距离呢?
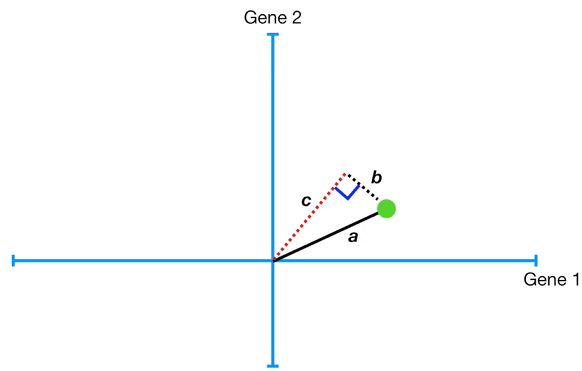
先看一个点的投射
这个数据点到原点的距离是不变的,记为a,其到直线的距离记为b,而投射点到原点的距离记为c。根据勾股定理,如果直角边b变大的话,那么直角边就c会变小。
PS:很多其他资料介绍PCA原理时提到的最大方差理论和最小平方误差理论都是基于这个道理的
实际上计算c会简单一些,所以PCA一般是通过计算所有数据点到原点距离平方和sum()最大值来寻找最优解。
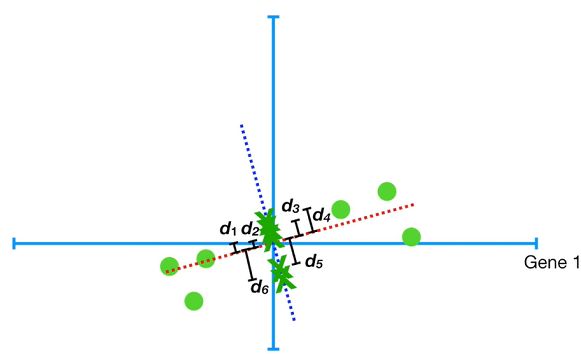
如下图所示,分别将这6个样本的投射点到原点距离标记为d1,d2,...,d6,然后计算这些点的平方和,这些平方和也被称为SS距离,即。
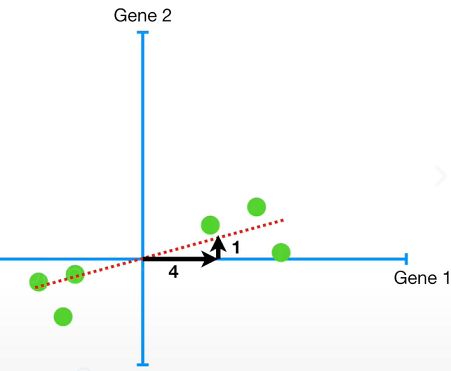
获得SS最大值时的这条线,被称为PC1。假设PC1这条线的斜率为0.25,这意味着每当我们在Gene1前进4个单位时,PC1上的数据点在Gene2上就增加1个单位。
这也意味着这几个样本在Gene1上更加分散,而在Gene2上分散程度较小。
根据鸡尾酒配方来思考PC1,为生成PC1,我们加入了4份Gene1和1份Gene2,这也说明在描述数据的分散程度方面,Gene1更加重要。
在数学上,这种鸡尾酒配方被称为Gene1和Gene2的线性组合,或也可以说“PC1是几个变量的线性组合”。
特征值、奇异值、特征向量和载荷分数
在PCA中,将SS称为PC1的特征值(Eigenvalue);PC1特征值的平方被称为PC1的奇异值(Singular Value)。
根据上面的假设,PC1的斜率为0.25,如果下图的红色箭头是一个长度单位,那么它是有0.97个Gene1和0.242个Gene2构成,所以被称为特征向量(Eigenvector)或奇异向量(Singular vector)。
而每个基因的比例,被称为PC1的载荷分数(loading score)
PC2计算原理
在二维坐标中,PC2是一条通过原点,并且与PC1垂直的直线。
很容易计算出PC2的斜率为-4,那么PC2就是由-0.242个Gene1和0.97个Gene2构成了。
同时,我们也可以计算出PC2的特征值。
绘制PCA图
旋转坐标轴,将PC1水平,PC2垂直。黑色叉表示原始的样本6,那么在新的坐标系中,Sample6的分布如下图所示。
变异度
各个主成分的变异度(Variation)计算,方法是SS除以样本减1。
假如上面那个案例中PC1变异度为15,PC2的变异度为3,那么总变异度为18.
因此PC1在总变异中所占的比值为83%,PC2占的总变异为17%。
多维数据
如果我们有3个基因,根据前面描述的步骤,分别找出PC1、PC2(垂直于PC1)和PC3(同时垂直于PC1和PC2),
理论上讲,主成分的数目等于变量数目或样本数目二者较小的那个(后面会有扩展)
同时也可以计算出各个主成分的变异度。
在上面的案例中,只使用PC1和PC2可以解释94%的变异度,所以我们只保留PC1和PC2最终绘图
这样,我们就获得了最终降维之后的结果。
扩展
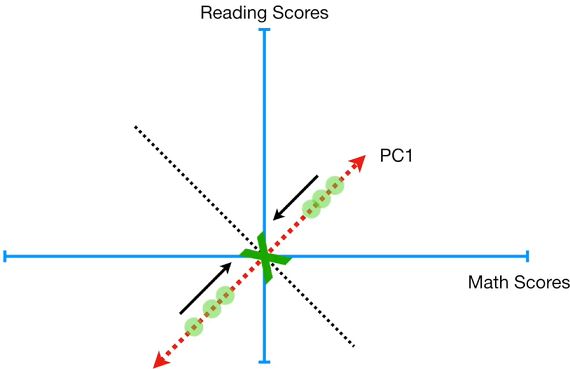
标准化数据
在进行PCA降维之前,需要确保所有数据处于同一标准下。
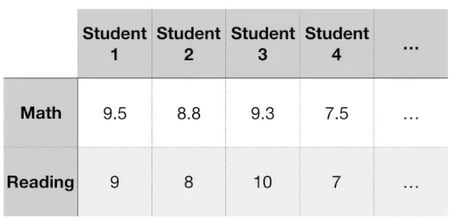
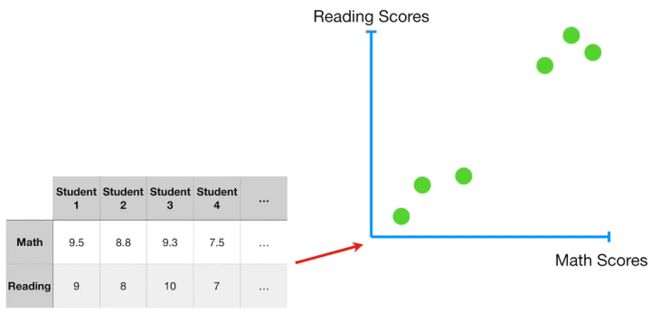
例如下面这组数据,Math分数是按照百分制统计,而Reading分数是按照十分制统计。
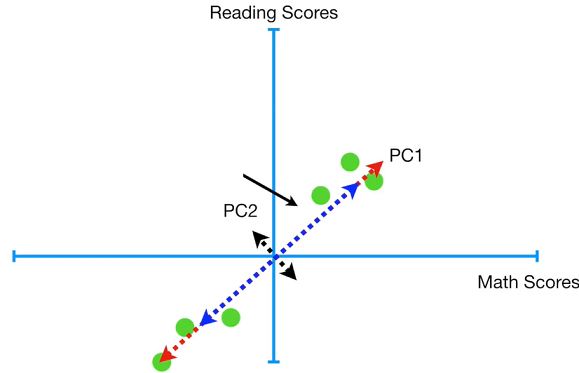
那么我们在计算PC1时可能会得到PC1由0.99个Math和0.1个Reading组成,但是这仅仅是由于Math分数本身就是Reading分数的10倍。
所以我们需要首先将每一个变量除以其所在组的标准差进行标准化处理。
主成分数
A
上面的那个案例中,我们只有两组观测数据。
绘制完PC1和PC2后,还可以绘制出PC3吗?
根据之前的讲述,PC3是同时垂直于PC1和PC2的。
那么绘制PC3时,基于已有的数据,先去寻找垂直于PC1的直线,只会得到PC2。
寻找垂直于PC2的直线,也只会得到PC1。
所以无法绘制出PC3。
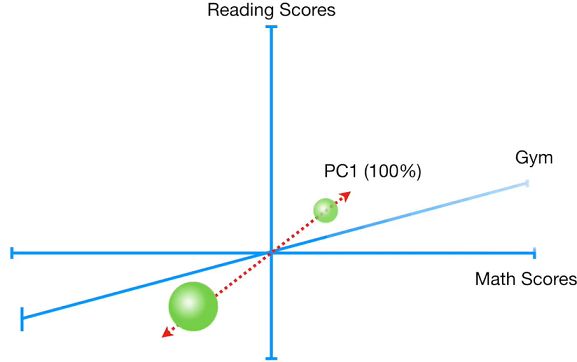
B
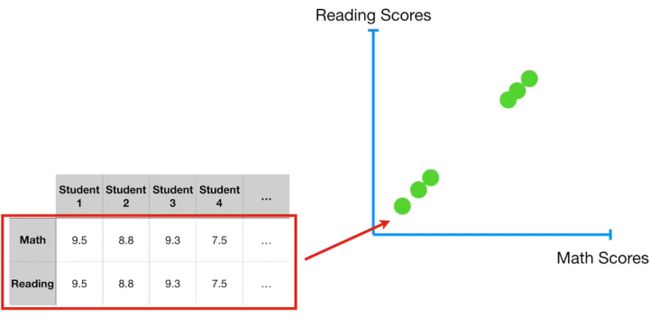
如果上面的案例中,Math和Reading是100%相关的.
绘制完PC1后,绘制一条垂直于PC1的PC2时发现,所有的数据投射在PC2的点都是原点,即特征值为0。
这时,PC1能够100%解释所有的变异。所以此时仅有PC1一个主成分。
C
如果学生数目减少为2,那么数据的分布在二维平面只有2个点,
2个点仅可以构成一条直线,所以PC2的特征值必然为0。
即使增加一个观测指标Gym,如果只有两个学生的话,最终数据在三维空间只有两个点,所以也只会有一个主成分PC1。
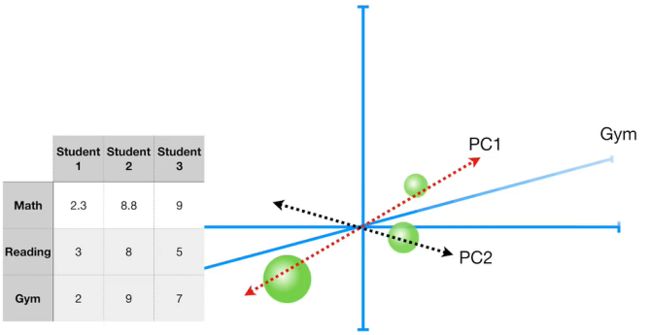
D
扩展一下,如果数据变为3个学生和3个观测指标,最终会有几个主成分呢?
3个学生会产生3个数据点,3点构成一个平面(平面是二维的),所以PC3的特征值必然为0。
因此会产生2个主成分PC1和PC2。
所以,一组数据进行降维分析时,主成分数最终等于变量数目或样本数目(二者较小的那个),但是上限是特征值大于0的PC数。
申明
本文是根据StatQuest系列视频整理而来
已获得Josh Starmer授权说明
感谢久久琼殷不辞辛苦将视频转载至B站