开篇之前,
我想问你一个问题:
如何用数学的方法表白?
文学家们用文字,音乐家们用旋律,至少这些还是我们可以理解的,周围一堆数学高手,好奇那些看着乏味的数学家们会如何表白呢?
据说在1650年的斯德哥尔摩街头,笛卡尔52岁时邂逅了18岁的瑞典公主克里斯汀,他成了公主的数学老师。
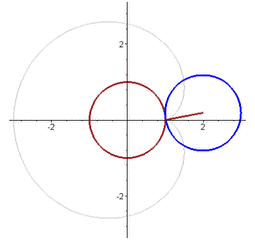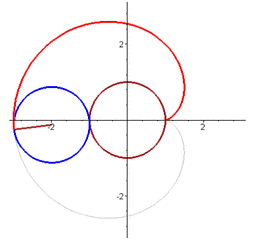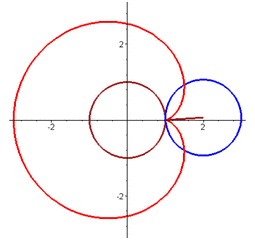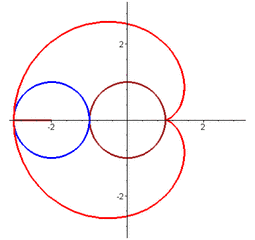
后来,笛卡尔被流放回法国,总共给公主寄出过13封情书,也就是在最后一封信中,只有短短的一个数学公式:r = a(1-sinθ)
你知道它是什么意思吗?
而这位公主呢,她恰好是个低调的数学迷,她一眼就看破了其中真意,于是优雅的在纸上,在直角坐标系中将曲线画了出来,于是一个心形图案跃然纸上。
这封享誉世界的另类情书,至今,还保存在欧洲笛卡尔的纪念馆里。
浪不浪漫!有没有一种数学家独特的浪漫,是不是另一种不同的美!是不是对数形结合有了一个感性的认识?
1
数形结合思想
具体讲数形结合思,想就不得不再说道上文中的——“笛卡尔”,自从欧几里德的《几何原本》问世以来,人们一直把代数限定在研究数及其关系的范畴内,把几何限定在研究位置和图形的范畴内。
代数和几何截然分家持续了几千年,犹如两座高山被万丈深渊分割,连接代数和几何的桥梁将“数”和“形”紧密联系在一起的科学就是笛卡儿创立的坐标几何学,数形结合思想就此产生。
笛卡儿创立坐标几何学
数学思想方法可以说是数学的灵魂和精髓,而数形结合思想是数学解题当中最常用、最重要的数学思想方法之一,也是初中学生必须娴熟掌握的数学技能之一。
数与形是数学中两个最古老、最基本的元素,是数学大厦深处的两块基石,所有的数学问题都是围绕数和形的提炼、演变、发展而展开的:每一个几何图形中都蕴藏着一定的数量关系,而数量关系又常常可以通过图形的直观性作出形象的描述。
因此,在解决数学问题时,常常根据数学问题的条件和结论之间的内在联系,将数的问题利用形来观察,提示其几何意义;而形的问题也常借助数去思考,分析其代数含义。
如此将数量关系和空间形式巧妙地结合起来,并充分利用这种“结合”,寻找解题思路,使问题得到解决的方法。
简言之,就是把数学问题中的数量关系和空间形式相结合起来加以考察的处理数学问题的方法,称之为数形结合的思想方法。
我国著名数学家华罗庚曾说:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”。
数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来, 通过"以形助数"或"以数解形"即通过抽象思维与形象思维的结合,可以使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的。
2
解决哪些问题
数形结合的思想方法是数学学习的主线之一,应用数形结合的思想解题,不仅直观易于寻找解题途径,而且能避免繁杂的计算和推理,简化解题过程。具体可以解决以下问题:
解决函数、方程与不等式、三角函数、线性规划、数列、解析几何、立体几何、绝对值、分数应用等问题。
在运用数形结合思想分析和解决问题时,要注意三点:
1、要彻底明白一些基础概念和运算的几何意义以及函数图象的代数特征;
2、恰当设未知数建立关系,由数思形,以形想数,做好数形转化;
3、正确确定未知数的取值范围。
3
具体应用方法
作为一种 数学思想方法,数形结合的应用大致又可分为两种情形:
一是借助于数的精确性来阐明形的某些属性;
二是借助形的几何直观来阐明数间某种关系。
换句话说,数形结合包括三个方面:以数化形、以形变数、形数互变。
以数化形
由于“数”和“形”是一种对应,有些数量比较抽象,我们难以把握,因此我们可以把“数”的对应“形”找出来,利用图形来解决问题。
以形变数
虽然形有形象直观的优点,但在定量方面还必须借助代数的计算,充分利用图形的性质或几何意义,把“形”正确表示成“数”的形式,进行分析计算。
形数互变
在有些数学问题中不仅仅是简单的“以数变形”或“以形变数”而是需要形数互相变换,不但要想到由形的直观变为“数”的严密还要由“数”的严密联系到"形"的直观。
总之,数形结合是将抽象的数学语言与直观图形结合起来,不仅能直观地发现解题的途径,而且能避免复杂的计算与推理,大大简化解题的过程。
4
中学考点分析
在初中数学中数形结合思想贯穿整个教材的始终,诸如:在学习二次函数、代数、三角形等问题中都运用到了数与形状的结合。
可以说数形结合的思想方法是解决初中数学问题乃至高中、大学、等等数学问题的一个通法,运用一秒存乎一心。
在做题中,要重视“数形结合”的思维训练,只要与“形”沾得上一点边,就应该根据题意画出草图来分析一番。
这样做,不但直观,而且全面,整体性强,容易找出切入点,对解题大有益处。
下面,青果教育研究院院长常性军老师结合具体考点,针对“数形结合”思想的具体运用,特别设计了这些经典题型,与你分享。希望同学们可以认真理解,做一道题,学会一类题,一步行,千里亦能行。
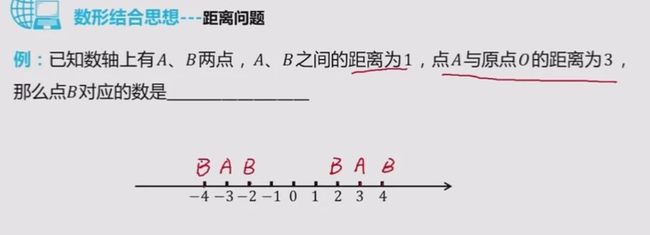
有理数
平面直角坐标系
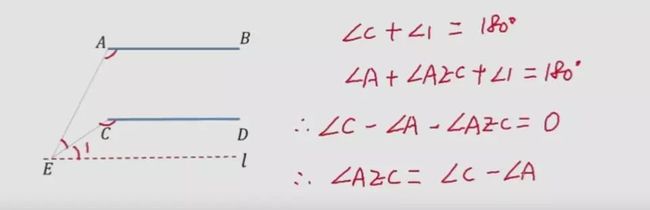
相交线与平行线
反比例函数
勾股定理
一次函数
总而言之,数形结合,是初中生不得不跨的坎,无它,因为数形结合在某种程度上来说是数学解题的捷径和钥匙,掌握了数形结合的思想,提高30分不是梦。
希望借此文让大家能认识到数形结合思想在中学数学解题中的重要性,对数学学习有所帮助!
文 小常老师 青果教育整理发布,转载请注明出处