哎,比预想的发布时间慢了一周多,曾慷慨激昂立下的flag,险些成为泡影。
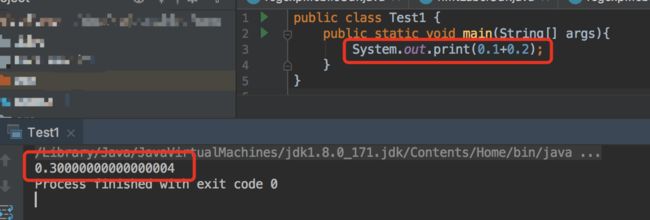
话不多说,进入正题,不知道有没有看到标题直接骂街的读者:“作者傻x吧,0.1+0.2怎么可能不等于0.3,小学没毕业吧”。别急,今天讨论的不是数学上的问题,而是计算机上的,我们先看下面几张图:
python:
js:
java:
scala:
上面几张图可以看出大部分语言都有这种情况,去网上搜索基本会得到这样的回答:由于精度问题,导致了结果不完全精确。但具体是怎么不准确,为何会有精度差异很少有人提起,今天就来彻底剖析一下来龙去脉。
我们分以下几点来说:
一、10进制和2进制的相互转化
1、2进制转10进制
2进制的110.11转换成10进制,计算方法是这样(小数点左边从右向左分别代表2的0,1,2...次方,小数点右边,从左往右数,分别代表2的-1,-2,-3...次方):
1*2^2 + 1*2^1 + 0*2^0 + 1*2^(-1) + 1*2^(-2) = 6.75 (2^x 代表2的x次方)
2、10进制转2进制
10进制的6.75转换成2进制:计算方法是这样的(把10进制的整数和小数部分分开来看,整数部分用除2取余逆序排列法转换二进制,小数部分用乘2取整顺序排列法转2进制):
①、整数部分
6 / 2 = 3……0(此结果代表商为3,余数为0)
3 / 2 = 1……1
1 / 2 = 0……1
将余数逆序排列,所以6的2进制表示为110。
我们来看下原理:其实这个也很好理解,可以把这个数看做是一串带系数的2的n次方的级数,设当前数为x,a[n]为系数,a[n]∈{0,1}
x = a[n]2^n + a[n-1]2^(n-1) + ... + a[0]*2^0
x / 2 的余数相当于a[0]
后面的系数以此类推,这就是除2逆序排列的原理。
②、小数部分
0.75 * 2 = 1 + 0.5 取整数部分1,0.5继续进入后面的循环,直到小数部分为0为止
0.5 * 2 = 1 + 0
于是0.75转换成2进制为0.11
为了后面的铺垫,再举个例子,10进制的0.2转2进制:
0.2 * 2 = 0 + 0.4
0.4 * 2 = 0 + 0.8
0.8 * 2 = 1 + 0.6
0.6 * 2 = 1 + 0.2
0.2 * 2 = 0 + 0.4
。。。
。。
。
发现没有,按照这个方式计算下去,会进入一个2、4、8、6、2。。。的循环,所以10进制的0.2用二进制表示为0.0011001100110011...
同样,我们看下原理,其实和整数部分的原理差不多,可以把这个数看做是一串带系数的2的n次方的级数,设当前数为x,a[n]为系数,a[n]∈{0,1},
x = a[-1]*2^(-1) + a[-2]*2^(-2) + ... + a[-n]*2^(-n)
x * 2 的整数部分相当于a[-1]
后面的系数以此类推,这就是乘2序排列的原理。
有人可能会有疑问,除去首项,其他所有项乘2再相加也能凑出整数部分啊,下面来做个证明从-2到-n项乘2再求和不可能有整数部分,证明为等比数列前n项和公式(如果这个也不懂,请参考百度错位相减法算等比数列前n项和),把-2项之后的所有项放大到最大,及a[n]均为1,则:
S = a[-2]2^(-2) + ... + a[-n]2(-n) = 2^(-2) + ... + 2^(-n) = 1/4 * (1-(1/2)^(n-1))/(1-1/2) <= 1/2,
当n趋于无穷时,等式可取等号,但是生活中,包括计算机中,都是有限项,无法取到等号,所有S<1/2,2S<1,可知-2至-n项求和再乘2无法得到整数部分。
二、程序是怎么处理浮点型的
1、整型的处理:
我们知道计算机中所有的数据信息都会被处理成2进制的数来表示:
以64整型来举例,共64位0或1,其中第一位表示符号(0为+,1为-),后面63位表示值的大小。
举个例子:
000...011 = 3 (长度为64个,省略的部分均为0)
100...011 = -3 (长度为64个,省略的部分均为0)
于是这样64位0或1,就可以表示整型了。
2、浮点型的处理
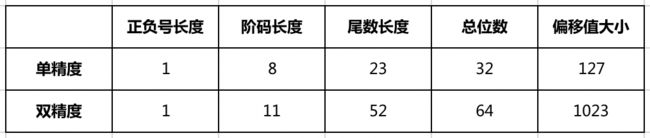
先上一张表和一张图:
上表分别是单精度和双精度的结构分布,上图则是对双精度的结构展示,下面就用这张图来解释上表的几个名词。
数符:上图的蓝色部分,就是决定数字是正还是负,当第一位是0时为正,是1时为负;
阶码:上图的黄色部分(第2~12位),共11位,为双精度的阶码,2的阶码次幂减去偏移值表示尾值处理后的实际值的小输掉的向左偏移位数(如果是负值,就是向右),好吧,这段听起来不像人话,容我后面举例解释;
尾值:上图的绿色部分(第13~64位),共52位,为双精度的小数部分;
偏移值:就是一个值,单精度就是127,双精度就是1023,先不用管它是怎么来的,他的作用就是让2的阶码次幂减的;
那基本都解释清楚了,那我们看下双精度的浮点型是如何表示的吧。
IEEE 754浮点数标准
这是一种浮点型的表示规范,为什么要有这个规范呢,举个例子:比如10进制的1.5,用2进制表示为1.1,现在我们要用科学计数法表示这个数字,
那我可以写成1.1*(2^0),也可以写成11*(2^(-1)),或者0.11*(2^1)
像上面这样,一个数字可以有多种表示方法,对于人们处理浮点型很不方便,甚至容易造成精度的不统一。为了解决这一问题,人们制定了IEEE 754浮点数标准,此规范规定浮点型都要写成
1.xxxxx*(2^xxxx)
的形式,即第一个数的开头恒定是“1.”,第二个数为2的n(n可以是负数)次方。
那我们看下一个浮点型怎么用64位0,1进行表示吧:
先做一些预设,设数符为a,阶码为b,尾值为c(c为[0,1)区间内的一个小数),偏移值为d,那任意一个浮点型x可表示为
x = (1+c)*(2^(b-d))
解释一下,因为第一项的数字开头恒定为“1.”,所以尾值可能省去表示1这个数字,这样尾值可以多出一位表示小数,用于提高精度。
举个例子:-4.75(2进制表示为100.11)的64位表示形式
数符:1(因为是负数);
尾值:0.0011(因为开头“1.”恒定);
偏移值:1023(双精度恒定为1023),这个值主要是是为了让阶码正负值都可以表示;
阶码:1025(减去偏移值之后为2);
(-1)*(1+0.0011)*2(1025-1023) = -100.11
看一下64位表示形式
1 10000000001 0011000000...00 省略的均为0。
再举个例子:0.2,前面提到的2进制表示为0.001100110011...,其中循环项0011
数符:0(因为是正数);
尾值:0.10011001011001...1010 (...代表1001的循环项);
偏移值:1023;
阶码:1020(减去阶码之后为-3);
这里单独对尾值做个说明:小数点后共52位,相当于是把0.2的2进制表示0.001100110011...的小数点向右移动了3位,移动到第一个非0数字之后,再取小数点后面的部分,但是这里要注意,因为小数点53位上是1,有一个舍入问题,程序会采取0舍1入的方法进行处理,我们看下49~53位的这几个数字 10011,现在要保留4位,采用0舍1入的原则,最终变成1010。
看一下64位的形式
0 01111111100 10011001...1010 省略的为1001循环项
三、0.1+0.2的计算
我们看上图,为几个数的浮点型经过位移后的表示形式,因为尾值最多有52个有效数字,加上开头恒定为“1.”,所以每个值一共有53个有效数字(即从左边第一个非0数字开始到结束,一共有53位),图中已用绿色标记,我们看下0.2舍入前后的区别,舍入之前0.2的第54位有效数字为1,所以保留53位时要进1,于是0.2的最后4位就成了1010了,0.1也是同样的道理。
此时我们把0.1和0.2对应位相加,如果等于2就进1,于是就得到了“0.1+0.2舍入前”,然后我们发现,此时有效数字又超过53个了,需要进一步做舍入操作,于是得到“0.1+0.2舍入后”,然后我们用乘2取整法算出0.3的表示,用0.3和0.1+0.2进行对比,发现前面完全一致,只有最后4位存在差异,这也就造成了0.1+0.2不等于0.3的原因了。
幸运的是,python中提供了内置hex()函数,用于进一步验证这个结论,先看下面一张图:
一点点来解释,hex函数是浮点型的小数点先位移到第一位有效数字之后,再将小数点后面的数字4个4个一组,转换成16进制来表示。
拿0.1的“0x1.999999999999ap-4”来举例:
0x代表是16进制的数字,p-4代表小数点向左移动4位(p+4代表向右移动4),然后主要看下中间的1.999999999999a,我们发现0.1的循环项1001的16进制刚好为9,而0.1的最后4位1010的16进制刚好为a(16进制中a代表10),这更加印证了我们前面的结论是没有错的。
来看下0.1+0.2(“0x1.3333333333334p-2”)与0.3(“0x1.3333333333333p-2”)在最后一位上确实存在差异,一个为4,一个为3,而这刚好是上面我们计算的0100与0011的差异。
四、解决方案
根据以上,我们也就不难理解日常工作中遇到的如下图一样的怪现象了:
在此提供一种解决方案,就是每次处理浮点型操作的时候,对结果进行符合自己精度要求四舍五入,则可以避免此类问题的发生,如下图操作。