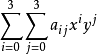本文作者:小嗷
微信公众号:aoxiaoji
吹比QQ群:736854977
链接:https://www.jianshu.com/u/45da1fbce7d0
[图片上传失败...(image-c0f823-1530856575202)]
[图片上传失败...(image-379db1-1530856575202)]
[图片上传失败...(image-8e3ead-1530856575202)]
在第31篇图像金字塔中,小嗷利用的pyrUp/pyrDown实现图片的放大和缩小(行和列偶数列去掉或者增加),这次打算用5种插值法实现图像压缩和放大
在本篇中,您将学习:
5种插值法的基本原理
本文你会找到以下问题的答案:
- 最近邻插值
- 双线性内插值算法
- 双三次插值
- 使用像素区域关系重新采样
- 兰索斯
- resize()
- Floor()
- Round()
2.1 理论
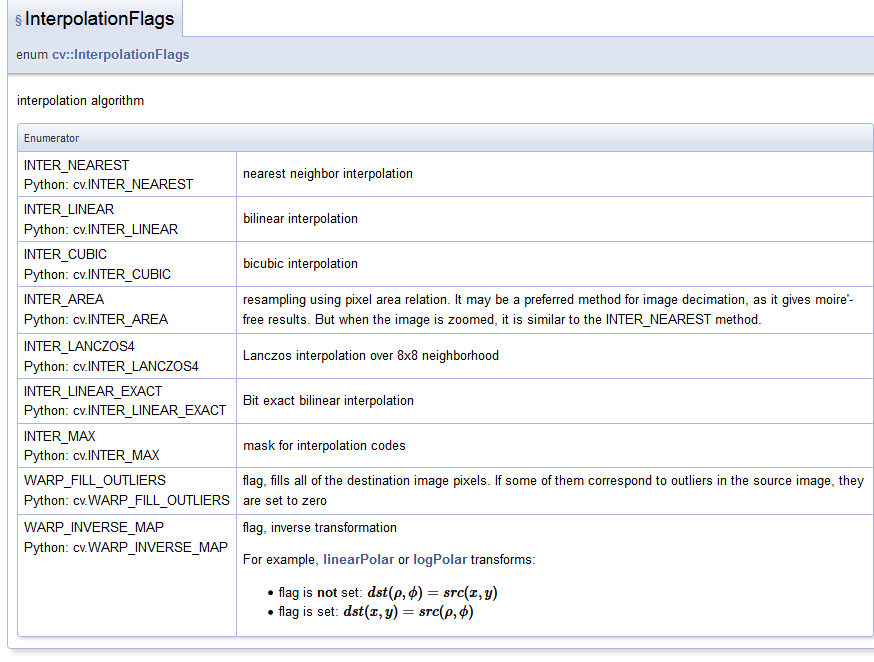
小嗷在官网查了查插值算法如下:
- INTER_NEAREST:最近邻插值
- INTER_LINEAR :双线性插值
- INTER_CUBIC :双三次插值
- INTERAREA :使用像素区域关系重新采样。它可能是一种首选的图像抽取方法,因为它提供了莫尔无结果。但是当图像被放大时,它与INTERNEAREST方法相似。(第一种相似)
- 兰索斯(Lanczos)插值大于8x8邻域
- INTERLINEAREXACT :一些精确的双线性插值
- INTER_MAX : 插值代码(对于掩膜)
- WARPFILLOUTLIERS :标志,填充所有目标图像像素。如果其中一些与源映像中的异常值对应,则将它们设置为零
- WARPINVERSEMAP 标志,逆变换.例如,线性极变换或对数极变换:
[图片上传失败...(image-99b79f-1530856575201)]
其中,下面几种算法涉及透视和仿射。所以,先不写。先介绍前面几种算法 如下:
2.2 简介及例子
图像的缩放很好理解,就是图像的放大和缩小。传统的绘画工具中,有一种叫做“放大尺”的绘画工具,画家常用它来放大图画。当然,在计算机上,我们不再需要用放大尺去放大或缩小图像了,把这个工作交给程序来完成就可以了。下面就来讲讲计算机怎么来放大缩小图象;在本文中,我们所说的图像都是指点阵图,也就是用一个像素矩阵来描述图像的方法,对于另一种图像:用函数来描述图像的矢量图,不在本文讨论之列。
越是简单的模型越适合用来举例子,我们就举个简单的图像:3X3 的256级灰度图,也就是高为3个象素,宽也是3个象素的图像,每个象素的取值可以是 0-255,代表该像素的亮度,255代表最亮,也就是白色,0代表最暗,即黑色。假如图像的象素矩阵如下图所示(这个原始图把它叫做源图,Source):
234 38 22
67 44 12
89 65 63
这个矩阵中,元素坐标(x,y)是这样确定的,x从左到右,从0开始,y从上到下,也是从零开始,这是图象处理中最常用的坐标系,就是这样一个坐标:
---------------------->X
|
|
|
|
|
∨
Y
如果想把这副图放大为 4X4大小的图像,那么该怎么做呢?那么第一步肯定想到的是先把4X4的矩阵先画出来再说,好了矩阵画出来了,如下所示,当然,矩阵的每个像素都是未知数,等待着我们去填充(这个将要被填充的图的叫做目标图,Destination):
? ? ? ?
? ? ? ?
? ? ? ?
? ? ? ?
然后要往这个空的矩阵里面填值了,要填的值从哪里来来呢?是从源图中来,好,先填写目标图最左上角的象素,坐标为(0,0),那么该坐标对应源图中的坐标可以由如下公式得出:
2.2.1 最临近插值算法(INTER_NEAREST)
[图片上传失败...(image-b25c61-1530856575200)]
dstY代表输出图Y的坐标,srcY代表原图Y的坐标,srcX、srcY同理。
好了,套用公式,就可以找到对应的原图的坐标了
(0(3/4),0(3/4))=>(00.75,00.75)=>(0,0)
找到了源图的对应坐标,就可以把源图中坐标为(0,0)处的234象素值填进去目标图的(0,0)这个位置了。
接下来,如法炮制,寻找目标图中坐标为(1,0)的象素对应源图中的坐标,套用公式:
(10.75,00.75)=>(0.75,0)
结果发现,得到的坐标里面竟然有小数,这可怎么办?计算机里的图像可是数字图像,象素就是最小单位了,象素的坐标都是整数,从来没有小数坐标。这时候采用的一种策略就是采用四舍五入的方法(也可以采用直接舍掉小数位的方法),把非整数坐标转换成整数,好,那么按照四舍五入的方法就得到坐标(1,0),完整的运算过程就是这样的:
(10.75,00.75)=>(0.75,0)=>(1,0)
那么就可以再填一个象素到目标矩阵中了,同样是把源图中坐标为(1,0)处的像素值38填入目标图中的坐标。
依次填完每个象素,一幅放大后的图像就诞生了,像素矩阵如下所示:
234 38 22 22
67 44 12 12
89 65 63 63
89 65 63 63
这种放大图像的方法叫做最临近插值算法,这是一种最基本、最简单的图像缩放算法,效果也是最不好的,放大后的图像有很严重的马赛克,缩小后的图像有很严重的失真;
效果不好的根源就是其简单的最临近插值方法引入了严重的图像失真,比如,当由目标图的坐标反推得到的源图的的坐标是一个浮点数的时候,采用了四舍五入的方法,直接采用了和这个浮点数最接近的象素的值,这种方法是很不科学的,当推得坐标值为 0.75的时候,不应该就简单的取为1,既然是0.75,比1要小0.25 ,比0要大0.75 ,那么目标象素值其实应该根据这个源图中虚拟的点四周的四个真实的点来按照一定的规律计算出来的,这样才能达到更好的缩放效果。
双线型内插值算法就是一种比较好的图像缩放算法,它充分的利用了源图中虚拟点四周的四个真实存在的像素值来共同决定目标图中的一个像素值,因此缩放效果比简单的最邻近插值要好很多。
opencv源码:
cv::Mat matSrc, matDst1, matDst2;
matSrc = cv::imread("lena.jpg", 2 | 4);
//创建二个图像空间,色彩为黑色
matDst1 = cv::Mat(cv::Size(800, 1000), matSrc.type(), cv::Scalar::all(0));
matDst2 = cv::Mat(matDst1.size(), matSrc.type(), cv::Scalar::all(0));
//原图像的列行除以输出图像的列行
double scale_x = (double)matSrc.cols / matDst1.cols;
double scale_y = (double)matSrc.rows / matDst1.rows;
//每列中3个通道
for (int i = 0; i < matDst1.cols; ++i)
{
//第一个为1 x 比例,第二个为2 x 比例,第三个3 x 比例
int sx = cvFloor(i * scale_x);
//比较sx与matSrc.cols - 1的大小,谁小取谁
sx = std::min(sx, matSrc.cols - 1);
//每行
for (int j = 0; j < matDst1.rows; ++j)
{
// /第一个为1 x 比例
int sy = cvFloor(j * scale_y);
//比较sy与matSrc.rows - 1的大小,谁小取谁
sy = std::min(sy, matSrc.rows - 1);
//将像素点设置给输出图像matDst1
matDst1.at(j, i) = matSrc.at(sy, sx);
}
}
cv::imwrite("nearest_1.jpg", matDst1);
cv::resize(matSrc, matDst2, matDst1.size(), 0, 0, 0);
cv::imwrite("nearest_2.jpg", matDst2);
2.2.2 双线性内插值算法(INTER_LINEAR)
双三次插值是一种更加复杂的插值方式,它能创造出比双线性插值更平滑的图像边缘。双三次插值方法通常运用在一部分图像处理软件、打印机驱动程序和数码相机中,对原图像或原图像的某些区域进行放大。Adobe Photoshop CS 更为用户提供了两种不同的双三次插值方法:双三次插值平滑化和双三次插值锐化。
在x y两个方向上分别进行一次线性插值,方向先后不影响顺序。
对于一个目的像素,设置坐标通过反向变换得到的浮点坐标为(i+u,j+v) (其中i、j均为浮点坐标的整数部分,u、v为浮点坐标的小数部分,是取值[0,1)区间的浮点数),则这个像素的值 f(i+u,j+v) 可由原图像中坐标为 (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定,即:
f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1)
[图片上传失败...(image-de38dd-1530856575200)]
其中f(i,j)表示源图像(i,j)处的的像素值,以此类推。
比如,像刚才的例子,现在假如目标图的象素坐标为(1,1),那么反推得到的对应于源图的坐标是(0.75 , 0.75), 这其实只是一个概念上的虚拟象素,实际在源图中并不存在这样一个象素,那么目标图的象素(1,1)的取值不能够由这个虚拟象素来决定,而只能由源图的这四个象素共同决定:(0,0)(0,1)(1,0)(1,1),而由于(0.75,0.75)离(1,1)要更近一些,那么(1,1)所起的决定作用更大一些,这从公式1中的系数uv=0.75×0.75就可以体现出来,而(0.75,0.75)离(0,0)最远,所以(0,0)所起的决定作用就要小一些,公式中系数为(1-u)(1-v)=0.25×0.25也体现出了这一特点
opencv源码:
uchar* dataDst = matDst1.data;
int stepDst = matDst1.step;
uchar* dataSrc = matSrc.data;
int stepSrc = matSrc.step;
int iWidthSrc = matSrc.cols;
int iHiehgtSrc = matSrc.rows;
for (int j = 0; j < matDst1.rows; ++j)
{
float fy = (float)((j + 0.5) * scale_y - 0.5);
int sy = cvFloor(fy);
fy -= sy;
sy = std::min(sy, iHiehgtSrc - 2);
sy = std::max(0, sy);
short cbufy[2];
cbufy[0] = cv::saturate_cast((1.f - fy) * 2048);
cbufy[1] = 2048 - cbufy[0];
for (int i = 0; i < matDst1.cols; ++i)
{
float fx = (float)((i + 0.5) * scale_x - 0.5);
int sx = cvFloor(fx);
fx -= sx;
if (sx < 0) {
fx = 0, sx = 0;
}
if (sx >= iWidthSrc - 1) {
fx = 0, sx = iWidthSrc - 2;
}
short cbufx[2];
cbufx[0] = cv::saturate_cast((1.f - fx) * 2048);
cbufx[1] = 2048 - cbufx[0];
for (int k = 0; k < matSrc.channels(); ++k)
{
*(dataDst+ j*stepDst + 3*i + k) = (*(dataSrc + sy*stepSrc + 3*sx + k) * cbufx[0] * cbufy[0] +
*(dataSrc + (sy+1)*stepSrc + 3*sx + k) * cbufx[0] * cbufy[1] +
*(dataSrc + sy*stepSrc + 3*(sx+1) + k) * cbufx[1] * cbufy[0] +
*(dataSrc + (sy+1)*stepSrc + 3*(sx+1) + k) * cbufx[1] * cbufy[1]) >> 22;
}
}
}
cv::imwrite("linear_1.jpg", matDst1);
cv::resize(matSrc, matDst2, matDst1.size(), 0, 0, 1);
cv::imwrite("linear_2.jpg", matDst2);
2.2.3 双三次:由相邻的4*4像素计算得出,公式类似于双线性(INTER_CUBIC)
在数值分析这个数学分支中,双三次插值(英语:Bicubic interpolation)是二维空间中最常用的插值方法。在这种方法中,函数f在点 (x,y) 的值可以通过矩形网格中最近的十六个采样点的加权平均得到,在这里需要使用两个多项式插值三次函数,每个方向使用一个。
双三次插值又叫双立方插值,用于在图像中“插值”(Interpolating)或增加“像素”(Pixel)数量/密度的一种方法。通常利用插值技术增加图形数据,以便在它打印或其他形式输出的时候,能够增大打印面积以及(或者)分辨率。
目前有不同的插值技术可供选用。双立方插值通常能产生效果最好,最精确的插补图形,但它速度也几乎是最慢的。“双线性插值”(Bilinear interpolation)的速度则要快一些,但没有前者精确。在商业性图像编辑软件中,经常采用的是速度最快,但也是最不准确的“最近相邻”(Nearest Neighbor)插值。其他一些插值技术通常只在高档或单独应用的程序中出现。
显然,无论技术多么高级,插补过的数据肯定没有原始数据准确。这意味着对一个图形文件进行插值处理后,虽然文件长度增加了(数据量增大),但不会有原先那幅图锐利,可能会在图形质量上打折扣。
公式
双三次插值通过下式进行计算:
[图片上传失败...(image-d47180-1530856575200)]
或者用一种更加紧凑的形式,
计算系数的过程依赖于插值数据的特性。如果已知插值函数的导数,常用的方法就是使用四个顶点的高度以及每个顶点的三个导数。一阶导数与表示 x 与 y 方向的表面斜率,二阶相互导数表示同时在 x 与 y 方向的斜率。这些值可以通过分别连续对 x 与 y 向量取微分得到。对于网格单元的每个顶点,将局部坐标(0,0, 1,0, 0,1 和 1,1)带入这些方程,再解这 16 个方程。
int iscale_x = cv::saturate_cast(scale_x);
int iscale_y = cv::saturate_cast(scale_y);
for (int j = 0; j < matDst1.rows; ++j)
{
float fy = (float)((j + 0.5) * scale_y - 0.5);
int sy = cvFloor(fy);
fy -= sy;
sy = std::min(sy, matSrc.rows - 3);
sy = std::max(1, sy);
const float A = -0.75f;
float coeffsY[4];
coeffsY[0] = ((A*(fy + 1) - 5*A)*(fy + 1) + 8*A)*(fy + 1) - 4*A;
coeffsY[1] = ((A + 2)*fy - (A + 3))*fy*fy + 1;
coeffsY[2] = ((A + 2)*(1 - fy) - (A + 3))*(1 - fy)*(1 - fy) + 1;
coeffsY[3] = 1.f - coeffsY[0] - coeffsY[1] - coeffsY[2];
short cbufY[4];
cbufY[0] = cv::saturate_cast(coeffsY[0] * 2048);
cbufY[1] = cv::saturate_cast(coeffsY[1] * 2048);
cbufY[2] = cv::saturate_cast(coeffsY[2] * 2048);
cbufY[3] = cv::saturate_cast(coeffsY[3] * 2048);
for (int i = 0; i < matDst1.cols; ++i)
{
float fx = (float)((i + 0.5) * scale_x - 0.5);
int sx = cvFloor(fx);
fx -= sx;
if (sx < 1) {
fx = 0, sx = 1;
}
if (sx >= matSrc.cols - 3) {
fx = 0, sx = matSrc.cols - 3;
}
float coeffsX[4];
coeffsX[0] = ((A*(fx + 1) - 5*A)*(fx + 1) + 8*A)*(fx + 1) - 4*A;
coeffsX[1] = ((A + 2)*fx - (A + 3))*fx*fx + 1;
coeffsX[2] = ((A + 2)*(1 - fx) - (A + 3))*(1 - fx)*(1 - fx) + 1;
coeffsX[3] = 1.f - coeffsX[0] - coeffsX[1] - coeffsX[2];
short cbufX[4];
cbufX[0] = cv::saturate_cast(coeffsX[0] * 2048);
cbufX[1] = cv::saturate_cast(coeffsX[1] * 2048);
cbufX[2] = cv::saturate_cast(coeffsX[2] * 2048);
cbufX[3] = cv::saturate_cast(coeffsX[3] * 2048);
for (int k = 0; k < matSrc.channels(); ++k)
{
matDst1.at(j, i)[k] = abs((matSrc.at(sy-1, sx-1)[k] * cbufX[0] * cbufY[0] + matSrc.at(sy, sx-1)[k] * cbufX[0] * cbufY[1] +
matSrc.at(sy+1, sx-1)[k] * cbufX[0] * cbufY[2] + matSrc.at(sy+2, sx-1)[k] * cbufX[0] * cbufY[3] +
matSrc.at(sy-1, sx)[k] * cbufX[1] * cbufY[0] + matSrc.at(sy, sx)[k] * cbufX[1] * cbufY[1] +
matSrc.at(sy+1, sx)[k] * cbufX[1] * cbufY[2] + matSrc.at(sy+2, sx)[k] * cbufX[1] * cbufY[3] +
matSrc.at(sy-1, sx+1)[k] * cbufX[2] * cbufY[0] + matSrc.at(sy, sx+1)[k] * cbufX[2] * cbufY[1] +
matSrc.at(sy+1, sx+1)[k] * cbufX[2] * cbufY[2] + matSrc.at(sy+2, sx+1)[k] * cbufX[2] * cbufY[3] +
matSrc.at(sy-1, sx+2)[k] * cbufX[3] * cbufY[0] + matSrc.at(sy, sx+2)[k] * cbufX[3] * cbufY[1] +
matSrc.at(sy+1, sx+2)[k] * cbufX[3] * cbufY[2] + matSrc.at(sy+2, sx+2)[k] * cbufX[3] * cbufY[3] ) >> 22);
}
}
}
cv::imwrite("cubic_1.jpg", matDst1);
cv::resize(matSrc, matDst2, matDst1.size(), 0, 0, 2);
那么具体什么实现呢?
假设源图像A大小为mn,缩放后的目标图像B的大小为MN。那么根据比例我们可以得到B(X,Y)在A上的的 对应坐标为A(x,y)=A(X(m/M),Y(n/N))。在双线性插值法中,我们选取A(x,y)的最近四个点。而在双立方 插值法中,我们选取的是最近的16个像素点作为计算目标图像B(X,Y)处像素值的参数。如图所示:
[图片上传失败...(image-af340d-1530856575199)]
如图所示P点就是目标图像B在(X,Y)处对应于源图像中的位置,P的坐标位置会出现小数部分,所以我们假设 P的坐标为P(x+u,y+v),其中x,y分别表示整数部分,u,v分别表示小数部分。那么我们就可以得到如图所示的 最近16个像素的位置,在这里用a(i,j)(i,j=0,1,2,3)来表示。
双立方插值的目的就是通过找到一种关系,或者说系数,可以把这16个像素对于P处像素值得影响因子找出 来,从而根据这个影响因子来获得目标图像对应点的像素值,达到图像缩放的目的。
[图片上传失败...(image-6ab1b-1530856575199)]
我们要做的就是求出BiCubic函数中的参数x,从而获得上面所说的16个像素所对应的系数。在学习双线性插 值法的时候,我们是把图像的行和列分开来理解的,那么在这里,我们也用这种方法描述如何求出a(i,j)对应 的系数kij。假设行系数为ki,列系数为k_j。我们以a00位置为例:
首先,我们要求出当前像素与P点的位置,比如第a00[即:第一个点(0.0)]-> P(x+u,y+v)->为(1+u,1+v)。
那么我们可以得到:k _ i _ 0=W(1+u),k _ j _ 0=W(1+v).
同理我们可以得到所有行和列对应的系数:
k_i_0=W(1+u), k_i_1=W(u), k__i_2=W(1-u), k_i_3=W(2-u);
k_j_0=W(1+v), k_j_1=W(v), k_j_2=W(1-v), k_j_3=W(2-v);
又是刚刚那个例子:
比如,像刚才的例子,现在假如目标图的象素坐标为(1,1),那么反推得到的对应于源图的坐标是(0.75 , 0.75), 这其实只是一个概念上的虚拟象素,实际在源图中并不存在这样一个象素,那么目标图的象素(1,1)的取值不能够由这个虚拟象素来决定,而只能由源图的这四个象素共同决定:(0,0)(0,1)(1,0)(1,1),而由于(0.75,0.75)离(1,1)要更近一些,那么(1,1)所起的决定作用更大一些,这从公式1中的系数uv=0.75×0.75就可以体现出来,而(0.75,0.75)离(0,0)最远,所以(0,0)所起的决定作用就要小一些,公式中系数为(1-u)(1-v)=0.25×0.25也体现出了这一特点
即:u 、v分别代表原图像的列(行)除以输出图像的列(行)
-
通过最近邻插值第一步求出u,v
//原图像的列行除以输出图像的列行 double scale_x = (double)matSrc.cols / matDst1.cols; double scale_y = (double)matSrc.rows / matDst1.rows; 再把u,v带入
[图片上传失败...(image-f7856e-1530856575198)]
得出所有行和列对应的系数:
k_i_0=W(1+u), k_i_1=W(u), k__i_2=W(1-u), k_i_3=W(2-u);
k_j_0=W(1+v), k_j_1=W(v), k_j_2=W(1-v), k_j_3=W(2-v);
这样我们就分别得到了行和列方向上的系数。 由k _ i _ j=k _ i*k _ j我们就可以得到每个像素a(i,j)对应的权值了。
3.最后通过求和公式可以得到目标图片B(X,Y)对应的像素值:
pixelB(X,Y)=pixelA(0,0)k00+pixelA(0,1)k01+…+pixelA(3,3)k3*3;
这里其实就是个求和公式,由于不知道怎么编辑公式,就这样表达了。
/**********************10-9*******************************
功能:双三次插值缩放图片
数学原理:假设原图像A的大小为m*n,新图像B的大小为M*N
如果我们要求B(X,Y)处的像素值:
我们首先可以得到B(X,Y)在图像A中对应的位置(x,y)=(X*(m/M),Y*(N/n))
这个时候求得的x,y是小数值,我们可以通过这个小数值坐标找到距离最近的16个像素点,
利用所选择的基函数,求出对应的每个像素的权值,最终获得pixelB(X,Y)
**********************************************************/
#include
#include
#include
using namespace std;
using namespace cv;
float a = -0.5;//BiCubic基函数
void getW_x(float w_x[4], float x);
void getW_y(float w_y[4], float y);
int main(){
Mat image = imread("lena.jpg");//源图像
float Row_B = image.rows*2;
float Col_B = image.cols*2;
Mat biggerImage(Row_B, Col_B, CV_8UC3);
for (int i = 2; i < Row_B-4; i++){
for (int j = 2; j < Col_B-4; j++){
float x = i*(image.rows / Row_B);//放大后的图像的像素位置相对于源图像的位置
float y = j*(image.cols / Col_B);
/*if (int(x) > 0 && int(x) < image.rows - 2 && int(y)>0 && int(y) < image.cols - 2){*/
float w_x[4], w_y[4];//行列方向的加权系数
getW_x(w_x, x);
getW_y(w_y, y);
Vec3f temp = { 0, 0, 0 };
for (int s = 0; s <= 3; s++){
for (int t = 0; t <= 3; t++){
temp = temp + (Vec3f)(image.at(int(x) + s - 1, int(y) + t - 1))*w_x[s] * w_y[t];
}
}
biggerImage.at(i, j) = (Vec3b)temp;
}
}
imshow("image", image);
imshow("biggerImage", biggerImage);
waitKey(0);
return 0;
}
/*计算系数*/
void getW_x(float w_x[4],float x){
int X = (int)x;//取整数部分
float stemp_x[4];
stemp_x[0] = 1 + (x - X);
stemp_x[1] = x - X;
stemp_x[2] = 1 - (x - X);
stemp_x[3] = 2 - (x - X);
w_x[0] = a*abs(stemp_x[0] * stemp_x[0] * stemp_x[0]) - 5 * a*stemp_x[0] * stemp_x[0] + 8 * a*abs(stemp_x[0]) - 4 * a;
w_x[1] = (a + 2)*abs(stemp_x[1] * stemp_x[1] * stemp_x[1]) - (a + 3)*stemp_x[1] * stemp_x[1] + 1;
w_x[2] = (a + 2)*abs(stemp_x[2] * stemp_x[2] * stemp_x[2]) - (a + 3)*stemp_x[2] * stemp_x[2] + 1;
w_x[3] = a*abs(stemp_x[3] * stemp_x[3] * stemp_x[3]) - 5 * a*stemp_x[3] * stemp_x[3] + 8 * a*abs(stemp_x[3]) - 4 * a;
}
void getW_y(float w_y[4], float y){
int Y = (int)y;
float stemp_y[4];
stemp_y[0] = 1.0 + (y - Y);
stemp_y[1] = y - Y;
stemp_y[2] = 1 - (y - Y);
stemp_y[3] = 2 - (y - Y);
w_y[0] = a*abs(stemp_y[0] * stemp_y[0] * stemp_y[0]) - 5 * a*stemp_y[0] * stemp_y[0] + 8 * a*abs(stemp_y[0]) - 4 * a;
w_y[1] = (a + 2)*abs(stemp_y[1] * stemp_y[1] * stemp_y[1]) - (a + 3)*stemp_y[1] * stemp_y[1] + 1;
w_y[2] = (a + 2)*abs(stemp_y[2] * stemp_y[2] * stemp_y[2]) - (a + 3)*stemp_y[2] * stemp_y[2] + 1;
w_y[3] = a*abs(stemp_y[3] * stemp_y[3] * stemp_y[3]) - 5 * a*stemp_y[3] * stemp_y[3] + 8 * a*abs(stemp_y[3]) - 4 * a;
}
估计要调用OpenCv-GPU加速类来加速一下,速度慢的要死
4、基于像素区域关系:共分三种情况,图像放大时类似于双线性插值,图像缩小(x轴、y轴同时缩小)又分两种情况,此情况下可以避免波纹出现。
opencv源码:
cv::resize(matSrc, matDst2, matDst1.size(), 0, 0, 3);
cv::imwrite("area_2.jpg", matDst2);
double inv_scale_x = 1\. / scale_x;
double inv_scale_y = 1\. / scale_y;
int iscale_x = cv::saturate_cast(scale_x);
int iscale_y = cv::saturate_cast(scale_y);
bool is_area_fast = std::abs(scale_x - iscale_x) < DBL_EPSILON && std::abs(scale_y - iscale_y) < DBL_EPSILON;
if (scale_x >= 1 && scale_y >= 1) //zoom out
{
if (is_area_fast) //integer multiples
{
for (int j = 0; j < matDst1.rows; ++j)
{
int sy = j * scale_y;
for (int i = 0; i < matDst1.cols; ++i)
{
int sx = i * scale_x;
matDst1.at(j, i) = matSrc.at(sy, sx);
}
}
cv::imwrite("area_1.jpg", matDst1);
return 0;
}
for (int j = 0; j < matDst1.rows; ++j)
{
double fsy1 = j * scale_y;
double fsy2 = fsy1 + scale_y;
double cellHeight = cv::min(scale_y, matSrc.rows - fsy1);
int sy1 = cvCeil(fsy1), sy2 = cvFloor(fsy2);
sy2 = std::min(sy2, matSrc.rows - 1);
sy1 = std::min(sy1, sy2);
float cbufy[2];
cbufy[0] = (float)((sy1 - fsy1) / cellHeight);
cbufy[1] = (float)(std::min(std::min(fsy2 - sy2, 1.), cellHeight) / cellHeight);
for (int i = 0; i < matDst1.cols; ++i)
{
double fsx1 = i * scale_x;
double fsx2 = fsx1 + scale_x;
double cellWidth = std::min(scale_x, matSrc.cols - fsx1);
int sx1 = cvCeil(fsx1), sx2 = cvFloor(fsx2);
sx2 = std::min(sx2, matSrc.cols - 1);
sx1 = std::min(sx1, sx2);
float cbufx[2];
cbufx[0] = (float)((sx1 - fsx1) / cellWidth);
cbufx[1] = (float)(std::min(std::min(fsx2 - sx2, 1.), cellWidth) / cellWidth);
for (int k = 0; k < matSrc.channels(); ++k)
{
matDst1.at(j, i)[k] = (uchar)(matSrc.at(sy1, sx1)[k] * cbufx[0] * cbufy[0] +
matSrc.at(sy1 + 1, sx1)[k] * cbufx[0] * cbufy[1] +
matSrc.at(sy1, sx1 + 1)[k] * cbufx[1] * cbufy[0] +
matSrc.at(sy1 + 1, sx1 + 1)[k] * cbufx[1] * cbufy[1]);
}
}
}
cv::imwrite("area_1.jpg", matDst1);
return 0;
}
//zoom in,it is emulated using some variant of bilinear interpolation
for (int j = 0; j < matDst1.rows; ++j)
{
int sy = cvFloor(j * scale_y);
float fy = (float)((j + 1) - (sy + 1) * inv_scale_y);
fy = fy <= 0 ? 0.f : fy - cvFloor(fy);
short cbufy[2];
cbufy[0] = cv::saturate_cast((1.f - fy) * 2048);
cbufy[1] = 2048 - cbufy[0];
for (int i = 0; i < matDst1.cols; ++i)
{
int sx = cvFloor(i * scale_x);
float fx = (float)((i + 1) - (sx + 1) * inv_scale_x);
fx = fx < 0 ? 0.f : fx - cvFloor(fx);
if (sx < 0) {
fx = 0, sx = 0;
}
if (sx >= matSrc.cols - 1) {
fx = 0, sx = matSrc.cols - 2;
}
short cbufx[2];
cbufx[0] = cv::saturate_cast((1.f - fx) * 2048);
cbufx[1] = 2048 - cbufx[0];
for (int k = 0; k < matSrc.channels(); ++k)
{
matDst1.at(j, i)[k] = (matSrc.at(sy, sx)[k] * cbufx[0] * cbufy[0] +
matSrc.at(sy + 1, sx)[k] * cbufx[0] * cbufy[1] +
matSrc.at(sy, sx + 1)[k] * cbufx[1] * cbufy[0] +
matSrc.at(sy + 1, sx + 1)[k] * cbufx[1] * cbufy[1]) >> 22;
}
}
}
cv::imwrite("area_1.jpg", matDst1);
5、兰索斯插值:由相邻的8*8像素计算得出,公式类似于双线性
具体原理请看维基百科:
https://en.wikipedia.org/wiki/Lanczos_resampling
opencv源码:
int iscale_x = cv::saturate_cast(scale_x);
int iscale_y = cv::saturate_cast(scale_y);
for (int j = 0; j < matDst1.rows; ++j)
{
float fy = (float)((j + 0.5) * scale_y - 0.5);
int sy = cvFloor(fy);
fy -= sy;
sy = std::min(sy, matSrc.rows - 5);
sy = std::max(3, sy);
const double s45 = 0.70710678118654752440084436210485;
const double cs[][2] = {{1, 0}, {-s45, -s45}, {0, 1}, {s45, -s45}, {-1, 0}, {s45, s45}, {0, -1}, {-s45, s45}};
float coeffsY[8];
if (fy < FLT_EPSILON) {
for (int t = 0; t < 8; t++)
coeffsY[t] = 0;
coeffsY[3] = 1;
} else {
float sum = 0;
double y0 = -(fy + 3) * CV_PI * 0.25, s0 = sin(y0), c0 = cos(y0);
for (int t = 0; t < 8; ++t)
{
double dy = -(fy + 3 -t) * CV_PI * 0.25;
coeffsY[t] = (float)((cs[t][0] * s0 + cs[t][1] * c0) / (dy * dy));
sum += coeffsY[t];
}
sum = 1.f / sum;
for (int t = 0; t < 8; ++t)
coeffsY[t] *= sum;
}
short cbufY[8];
cbufY[0] = cv::saturate_cast(coeffsY[0] * 2048);
cbufY[1] = cv::saturate_cast(coeffsY[1] * 2048);
cbufY[2] = cv::saturate_cast(coeffsY[2] * 2048);
cbufY[3] = cv::saturate_cast(coeffsY[3] * 2048);
cbufY[4] = cv::saturate_cast(coeffsY[4] * 2048);
cbufY[5] = cv::saturate_cast(coeffsY[5] * 2048);
cbufY[6] = cv::saturate_cast(coeffsY[6] * 2048);
cbufY[7] = cv::saturate_cast(coeffsY[7] * 2048);
for (int i = 0; i < matDst1.cols; ++i)
{
float fx = (float)((i + 0.5) * scale_x - 0.5);
int sx = cvFloor(fx);
fx -= sx;
if (sx < 3) {
fx = 0, sx = 3;
}
if (sx >= matSrc.cols - 5) {
fx = 0, sx = matSrc.cols - 5;
}
float coeffsX[8];
if (fx < FLT_EPSILON) {
for ( int t = 0; t < 8; t++ )
coeffsX[t] = 0;
coeffsX[3] = 1;
} else {
float sum = 0;
double x0 = -(fx + 3) * CV_PI * 0.25, s0 = sin(x0), c0 = cos(x0);
for (int t = 0; t < 8; ++t)
{
double dx = -(fx + 3 -t) * CV_PI * 0.25;
coeffsX[t] = (float)((cs[t][0] * s0 + cs[t][1] * c0) / (dx * dx));
sum += coeffsX[t];
}
sum = 1.f / sum;
for (int t = 0; t < 8; ++t)
coeffsX[t] *= sum;
}
short cbufX[8];
cbufX[0] = cv::saturate_cast(coeffsX[0] * 2048);
cbufX[1] = cv::saturate_cast(coeffsX[1] * 2048);
cbufX[2] = cv::saturate_cast(coeffsX[2] * 2048);
cbufX[3] = cv::saturate_cast(coeffsX[3] * 2048);
cbufX[4] = cv::saturate_cast(coeffsX[4] * 2048);
cbufX[5] = cv::saturate_cast(coeffsX[5] * 2048);
cbufX[6] = cv::saturate_cast(coeffsX[6] * 2048);
cbufX[7] = cv::saturate_cast(coeffsX[7] * 2048);
for (int k = 0; k < matSrc.channels(); ++k)
{
matDst1.at(j, i)[k] = abs((matSrc.at(sy-3, sx-3)[k] * cbufX[0] * cbufY[0] + matSrc.at(sy-2, sx-3)[k] * cbufX[0] * cbufY[1] +
matSrc.at(sy-1, sx-3)[k] * cbufX[0] * cbufY[2] + matSrc.at(sy, sx-3)[k] * cbufX[0] * cbufY[3] +
matSrc.at(sy+1, sx-3)[k] * cbufX[0] * cbufY[4] + matSrc.at(sy+2, sx-3)[k] * cbufX[0] * cbufY[5] +
matSrc.at(sy+3, sx-3)[k] * cbufX[0] * cbufY[6] + matSrc.at(sy+4, sx-3)[k] * cbufX[0] * cbufY[7] +
matSrc.at(sy-3, sx-2)[k] * cbufX[1] * cbufY[0] + matSrc.at(sy-2, sx-2)[k] * cbufX[1] * cbufY[1] +
matSrc.at(sy-1, sx-2)[k] * cbufX[1] * cbufY[2] + matSrc.at(sy, sx-2)[k] * cbufX[1] * cbufY[3] +
matSrc.at(sy+1, sx-2)[k] * cbufX[1] * cbufY[4] + matSrc.at(sy+2, sx-2)[k] * cbufX[1] * cbufY[5] +
matSrc.at(sy+3, sx-2)[k] * cbufX[1] * cbufY[6] + matSrc.at(sy+4, sx-2)[k] * cbufX[1] * cbufY[7] +
matSrc.at(sy-3, sx-1)[k] * cbufX[2] * cbufY[0] + matSrc.at(sy-2, sx-1)[k] * cbufX[2] * cbufY[1] +
matSrc.at(sy-1, sx-1)[k] * cbufX[2] * cbufY[2] + matSrc.at(sy, sx-1)[k] * cbufX[2] * cbufY[3] +
matSrc.at(sy+1, sx-1)[k] * cbufX[2] * cbufY[4] + matSrc.at(sy+2, sx-1)[k] * cbufX[2] * cbufY[5] +
matSrc.at(sy+3, sx-1)[k] * cbufX[2] * cbufY[6] + matSrc.at(sy+4, sx-1)[k] * cbufX[2] * cbufY[7] +
matSrc.at(sy-3, sx)[k] * cbufX[3] * cbufY[0] + matSrc.at(sy-2, sx)[k] * cbufX[3] * cbufY[1] +
matSrc.at(sy-1, sx)[k] * cbufX[3] * cbufY[2] + matSrc.at(sy, sx)[k] * cbufX[3] * cbufY[3] +
matSrc.at(sy+1, sx)[k] * cbufX[3] * cbufY[4] + matSrc.at(sy+2, sx)[k] * cbufX[3] * cbufY[5] +
matSrc.at(sy+3, sx)[k] * cbufX[3] * cbufY[6] + matSrc.at(sy+4, sx)[k] * cbufX[3] * cbufY[7] +
matSrc.at(sy-3, sx+1)[k] * cbufX[4] * cbufY[0] + matSrc.at(sy-2, sx+1)[k] * cbufX[4] * cbufY[1] +
matSrc.at(sy-1, sx+1)[k] * cbufX[4] * cbufY[2] + matSrc.at(sy, sx+1)[k] * cbufX[4] * cbufY[3] +
matSrc.at(sy+1, sx+1)[k] * cbufX[4] * cbufY[4] + matSrc.at(sy+2, sx+1)[k] * cbufX[4] * cbufY[5] +
matSrc.at(sy+3, sx+1)[k] * cbufX[4] * cbufY[6] + matSrc.at(sy+4, sx+1)[k] * cbufX[4] * cbufY[7] +
matSrc.at(sy-3, sx+2)[k] * cbufX[5] * cbufY[0] + matSrc.at(sy-2, sx+2)[k] * cbufX[5] * cbufY[1] +
matSrc.at(sy-1, sx+2)[k] * cbufX[5] * cbufY[2] + matSrc.at(sy, sx+2)[k] * cbufX[5] * cbufY[3] +
matSrc.at(sy+1, sx+2)[k] * cbufX[5] * cbufY[4] + matSrc.at(sy+2, sx+2)[k] * cbufX[5] * cbufY[5] +
matSrc.at(sy+3, sx+2)[k] * cbufX[5] * cbufY[6] + matSrc.at(sy+4, sx+2)[k] * cbufX[5] * cbufY[7] +
matSrc.at(sy-3, sx+3)[k] * cbufX[6] * cbufY[0] + matSrc.at(sy-2, sx+3)[k] * cbufX[6] * cbufY[1] +
matSrc.at(sy-1, sx+3)[k] * cbufX[6] * cbufY[2] + matSrc.at(sy, sx+3)[k] * cbufX[6] * cbufY[3] +
matSrc.at(sy+1, sx+3)[k] * cbufX[6] * cbufY[4] + matSrc.at(sy+2, sx+3)[k] * cbufX[6] * cbufY[5] +
matSrc.at(sy+3, sx+3)[k] * cbufX[6] * cbufY[6] + matSrc.at(sy+4, sx+3)[k] * cbufX[6] * cbufY[7] +
matSrc.at(sy-3, sx+4)[k] * cbufX[7] * cbufY[0] + matSrc.at(sy-2, sx+4)[k] * cbufX[7] * cbufY[1] +
matSrc.at(sy-1, sx+4)[k] * cbufX[7] * cbufY[2] + matSrc.at(sy, sx+4)[k] * cbufX[7] * cbufY[3] +
matSrc.at(sy+1, sx+4)[k] * cbufX[7] * cbufY[4] + matSrc.at(sy+2, sx+4)[k] * cbufX[7] * cbufY[5] +
matSrc.at(sy+3, sx+4)[k] * cbufX[7] * cbufY[6] + matSrc.at(sy+4, sx+4)[k] * cbufX[7] * cbufY[7] ) >> 22);// 4194304
}
}
}
cv::imwrite("Lanczos_1.jpg", matDst1);
cv::resize(matSrc, matDst2, matDst1.size(), 0, 0, 4);
cv::imwrite("Lanczos_2.jpg", matDst2);
以上代码的实现结果与cv::resize函数相同,但是执行效率非常低,只是为了详细说明插值过程。OpenCV中默认采用C++ Concurrency进行优化加速,你也可以采用TBB、OpenMP等进行优化加速。
注意:小嗷调用https://github.com/fengbingchun/OpenCVTest 中的resize函数,在OpenCVTest/src/include/resize.hpp中,里面实现代码我是从OpenCV中提取出来的,不依赖OpenCV,
这5种算法,一种比一种好。但是,需要耗费的时间是越好的处理时间越长。
3.1 Floor()
将浮点数四舍五入到不大于原始整数的最近整数。
C: int cvFloor(double value)
函数计算一个整数i这样:
3.2 Resize()
改变图像的大小
void resize(InputArray src, OutputArray dst, Size dsize, double fx=0, double fy=0, int interpolation=INTER_LINEAR );
参数介绍:
src:输入,原图像,即待改变大小的图像;
dst:输出,改变大小之后的图像,这个图像和原图像具有相同的内容,只是大小和原图像不一样而已;
-
dsize:输出图像的大小。如果这个参数不为0,那么就代表将原图像缩放到这个Size(width,height)指定的大小;如果这个参数为0,那么原图像缩放之后的大小就要通过下面的公式来计算:
dsize = Size(round(fx*src.cols), round(fy*src.rows))
其中,fx和fy就是下面要说的两个参数,是图像width方向和height方向的缩放比例。
fx:width方向的缩放比例,如果它是0,那么它就会按照(double)dsize.width/src.cols来计算;
fy:height方向的缩放比例,如果它是0,那么它就会按照(double)dsize.height/src.rows来计算;
-
interpolation:这个是指定插值的方式,图像缩放之后,肯定像素要进行重新计算的,就靠这个参数来指定重新计算像素的方式,有以下几种:
INTER_NEAREST - 最邻近插值 INTER_LINEAR - 双线性插值,如果最后一个参数你不指定,默认使用这种方法 INTER_AREA - resampling using pixel area relation. It may be a preferred method for image decimation, as it gives moire’-free results. But when the image is zoomed, it is similar to the INTER_NEAREST method. INTER_CUBIC - 4x4像素邻域内的双立方插值 INTER_LANCZOS4 - 8x8像素邻域内的Lanczos插值
使用注意事项:
-
dsize和fx/fy不能同时为0,要么你就指定好dsize的值,让fx和fy空置直接使用默认值,就像
resize(img, imgDst, Size(30,30));
要么你就让dsize为0,指定好fx和fy的值,比如fx=fy=0.5,那么就相当于把原图两个方向缩小一倍!
-
至于最后的插值方法,正常情况下使用默认的双线性插值就够用了。
几种常用方法的效率是:最邻近插值>双线性插值>双立方插值>Lanczos插值;
但是效率和效果成反比,所以根据自己的情况酌情使用。
正常情况下,在使用之前dst图像的大小和类型都是不知道的,类型从src图像继承而来,大小也是从原图像根据参数计算出来。但是如果你事先已经指定好dst图像的大小,那么你可以通过下面这种方式来调用函数:
resize(src, dst, dst.size(), 0, 0, interpolation);
3.3 Round()
将浮点数转到最近的整数。
[图片上传失败...(image-e5b64a-1530856575193)]
本篇文章的代码如下所示。
#include
#include
#include
#include
using namespace cv;
using namespace std;
void ResizeExample(Mat srcImage)
{
//判断输入有效性
CV_Assert(srcImage.data != NULL);
imshow("srcImage", srcImage);
Mat dstImage(256, 256, CV_8UC3);
//测试1:默认参数为双线性插值
double tTime;
tTime = (double)getTickCount();
const int nTimes = 100;
for (int i = 0; i < nTimes; i++)
{
resize(srcImage, dstImage, dstImage.size(), 0, 0);
}
tTime = 1000 * ((double)getTickCount() - tTime) / getTickFrequency();
tTime /= nTimes;
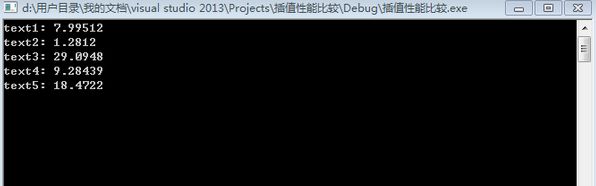
cout << "text1: " << tTime << endl;
imshow("1 default parameters:dstImage", dstImage);
//测试2:最邻近插值
tTime = (double)getTickCount();
for (int i = 0; i < nTimes; i++)
{
resize(srcImage, dstImage,Size(256,256), 0, 0,INTER_NEAREST);
}
tTime = 1000 * ((double)getTickCount() - tTime) / getTickFrequency();
tTime /= nTimes;
cout << "text2: " << tTime << endl;
imshow("2 INTER_NEAREST:dstImage", dstImage);
//测试3:像素区域插值
tTime = (double)getTickCount();
for (int i = 0; i < nTimes; i++)
{
resize(srcImage, dstImage, Size(256,256), 0.5, 0.5,INTER_AREA);
}
tTime = 1000 * ((double)getTickCount() - tTime) / getTickFrequency();
tTime /= nTimes;
cout << "text3: " << tTime << endl;
imshow("3 INTER_AREA : dstImage", dstImage);
//测试4:三次插值
tTime = (double)getTickCount();
for (int i = 0; i < nTimes; i++)
{
resize(srcImage, dstImage, Size(), 0.5, 0.5, INTER_CUBIC);
}
tTime = 1000 * ((double)getTickCount() - tTime) / getTickFrequency();
tTime /= nTimes;
cout << "text4: " << tTime << endl;
imshow("4 INTER_CUBIC : dstImage", dstImage);
//测试5:三次插值
tTime = (double)getTickCount();
for (int i = 0; i < nTimes; i++)
{
resize(srcImage, dstImage, Size(), 0.5, 0.5, INTER_LANCZOS4);
}
tTime = 1000 * ((double)getTickCount() - tTime) / getTickFrequency();
tTime /= nTimes;
cout << "text5: " << tTime << endl;
imshow("5 INTER_LANCZOS4 : dstImage", dstImage);
}
int main()
{
Mat srcImage = imread("D:\\1.jpg");
if (!srcImage.data)
return -1;
ResizeExample(srcImage);
waitKey(0);
return 0;
}
耗时:
效果图:
[图片上传失败...(image-553db4-1530856575193)]
- 本人是抱着玩一玩的心态,学习opencv(其实深度学习没有外界说的这么高深,小嗷是白板,而且有工作在身并且于代码无关)
- 大家可以把我的数学水平想象成初中水平,毕竟小嗷既不是代码靠吃饭又不是靠数学吃饭,毕业N年
- 写文章主要是为了后人少走点弯路,多交点朋友,一起学习
- 如果有好的图像识别群拉我进去QQ:631821577
- 就我一个白板,最后还是成的,你们别怕,慢慢来吧
分享可以无数次,转载成自己文章QQ邮箱通知一下,未经授权请勿转载。
邮箱:[email protected]
QQ群:736854977
有什么疑问公众号提问,下班或者周六日回答,ths
感言
本来小嗷想着插值算法全写,撸着撸着,再看看维基百科。小嗷发现不行,如果
全部插值算法从理解 -> 数学实现 -> 解刨opencv源码 -> 自己实现相关代码 -> CPU加速器(硬件加速) -> 成品
估计文章至少15W+字,目测要耗时1个月吧。就这么算的886,反正以后会写到GPU加速,下期见(本文3W2字,建议大家PC电脑上看)
推荐文章:
31.图像金字塔(pyrUp/pyrDown/高斯金字塔)
代码链接:
https://pan.baidu.com/s/1yJUkC7sYcs1n-9EZTpty6A
密码: ccsx