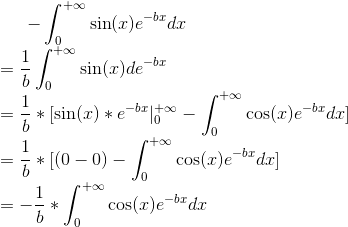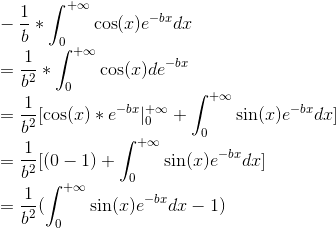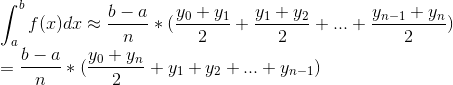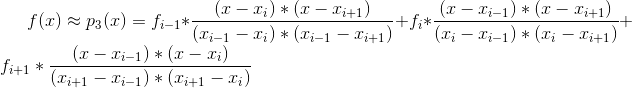本章涉及知识点
1、求解定积分存在的问题
2、研究案例之f(x)=sin(x)/x的定积分和广义积分
3、纯数学推导计算f(x)=sin(x)/x的广义积分
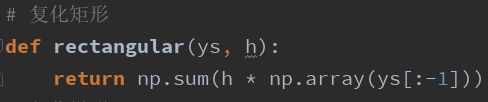
4、复化矩形算法
5、复化梯形算法
6、复化抛物线算法
7、三种定积分复化近似算法的编程实现
8、加入蒙特卡洛算法和高斯求积算法
9、不同近似算法计算f(x)=sin(x)/x的定积分结果比较
一、求解定积分存在的问题
由微积分我们知道,如果函数f(x)的原函数为F(x),则函数f(x)在闭区间[a,b]的定积分可以由牛顿-莱布尼兹公式计算出来
上式也称之为微积分的基本公式,它表明了:一个连续函数在区间[a,b]上的定积分等于它的任意一个原函数在区间[a,b]上的增量
但是实际问题中常常会遇到如下一些情况:
(1)、f(x)的表达式非常复杂,导致推导原函数F(x)变得更加困难
(2)、f(x)的原函数F(x)根本不能用初等函数来表示或者F(x)根本推导不出来
(3)、无法知道f(x)的精确表达式,只能以实验的方法观测出其若干个点对应的值
对于上述的情况,要计算f(x)的定积分就无法使用牛顿-莱布尼兹公式计算,例如f(x)=sin(x)/x就属于上述第二种情况,这时候我们就需要从定积分的定义原理出发,通过数值算法来计算其近似值
二、研究案例之f(x)=sin(x)/x的定积分和广义积分
来研究以下案例
需要计算f(x)的定积分或者广义积分
在数学物理的研究方法中,这个函数已经多次出现过,求解这个积分的算法也非常巧妙,而每次解法的思路,总是精妙又差别很大,可以说是涵盖了物理方法中很大一部分内容,比如复变函数、傅里叶变换以及拉普拉斯变换等的数学知识,这真是一个有趣的积分
显然,f(x)有精确的表达式,可是它的原函数F(x)的推导却非常困难,因为F(x)无法用初等函数来表示,下面我们首先用纯数学方法来推导f(x)的广义积分
三、纯数学推导计算f(x)=sin(x)/x的广义积分
原广义积分可以写为
计算一边的积分即可,为此我们模拟拉普拉斯变换的算法思想,构造出一个函数F(b),并顺利引入指数函数e来替换拉普拉斯变化里的虚数
显然,当b=0时
故我们只需要推导出F(b)的表达式即可,下面对F(b)求一阶导数(注意因变量是b,不是x)
下面我们需要推导上式积分,这里需要使用一次分部积分算法
我们对结果再使用一次分部积分算法
通过两次分部积分算法,我们得出
合并左右相同的积分项,可以解出
带入F(b)的导数表达式
至此我们推导出了F(b)的导数表达式,为了推导F(b)的表达式,我们对其导数进行一次不定积分计算
显然上式被积函数的原函数可以表示为反正切初等函数,即
至此,我们推导出了构造函数F(b)的表达式
又因为:
则可以计算出常数C
由之前的分析
带入F(0)即可计算出f(x)的广义积分
可以看到,纯数学的解法思路需要构造新函数,求导,两次分部积分算法和求不定积分的原函数来表示求解的定积分,而我们的计算机是不会自己推理这一系列数学推导的
四、复化矩形算法
从纯数学推导f(x)的定积分的算法中,显然不适合计算机,为此我们需要从定积分的原理出发
因为f(x)在区间[a,b]上连续可导,我们将区间[a,b]进行n等分,得到一系列的分点序列
而每一个小区间的长度为
而对于任意确定的正整数n,有
记
则定积分的近似计算可以表示为
上式就是复化矩形的算法,其几何意义为:用窄条矩形的面积作为窄条曲边梯形的面积的近似值,而整体上运用了台阶形的面积来作为曲边梯形面积的近似值
五、复化梯形算法
同理,复化梯形算法的几何意义为:将曲线f(x)上的一小段弧度用直线代替,也就是以直代取的思想,将窄条曲边梯形用窄条梯形近似替代
六、复化抛物线算法
同理,复化抛物线算法的几何意义为:将曲线f(x)上的两个小弧度用过这三个点的抛物线y=px^2+qx+r来代替
由Lagrange抛物线插值算法,我们用n=3的多项式来逼近任意一段抛物线
则f(x)的定积分可以推导为
至此,我们从定积分的原理出发,得到了3种近似计算定积分的算法,而计算机非常适合计算这些近似算法
七、三种定积分复化近似算法的编程实现
我们将上述近似算法代码化
八、加入蒙特卡洛算法
为了案例演示结果的比较,下面我们也加入蒙特卡洛算法来模拟计算定积分
九、不同近似算法计算f(x)=sin(x)/x的定积分结果比较
我们演示在[0,pi]区间内,不同算法计算f(x)=sin(x)/x的定积分结果为
可以看到复化梯形和抛物线算法计算结果的精度非常高
案例代码见:定积分的算法