前言
这篇笔记是StatQuest系列教程的第47,48,49节。第47节与第48节有很在一部分内容是重复的,主要讲的是层次聚类,第49节讲提K-means聚类。
热图简单案例
平时在读一个测序文章时,我们可能会经常看到热图,就像现在的这种图:
现在我们来解释一下这张图:
- 这是一张热图(heatmap),为什么要叫热图呢,因为它用不同的颜色来表示数值的大小,通常来说,用暖色(红色)表示数值大,冷色(蓝色)表示数值小。
- 这个热图的行(row)是基因名(可能太小看不清楚),列是RNA-seq的样本名。
- 当原始数据通过热图来展现时,数据经过了两种修饰来展示出来。第一种修饰就是相对丰度(relative abundances),以这种方式展示的数据,它研究的是一个基因在不同样本中的相对表达情况,这种展示方式,需要对同一行(也就是相同的基因在不同样本中的表达水平)的数据进行缩放(scaled),也就是Z转换。从下面的图中,我们就可以看到,样本1的某基因表达量明显高于其它样本(因为样本1的颜色最红,根据图例,它的表达值就最高),如下所示:
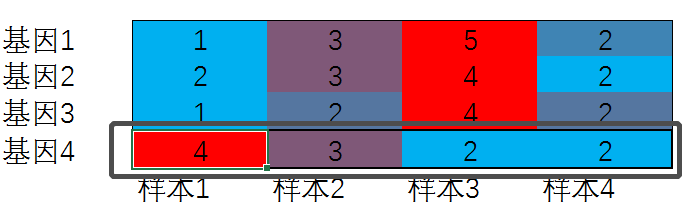
为了方便理解,我随手用Excel做了一下简陋的热图,如下所示:
可以看出,基因4在样本1中的表达量很高。不过按照第一种展示数据的方式,无法比较不同基因的表达水平差异,例如,在上图的黑色方框中,基因4显红色,这只能表达,样本1中基因4的表达水平比其它的样本高,不能说明样本1中的其它基因(例如基因3)的水平也比其它样本高,这种数据的展示方式只用于研究同一个基因在不同的样本中的表达水平差异。
第二处修饰后的展示方式就是根据这些基因表达的相似性,把它们放到一块,如下所示:
再看下面的图形:
从上到下,我们可以看到这些基因的表达的模式。
在第一个紫红色的方框中,我们可以看到,这些基因在第2个样本中表达水平最高,而在第4个样本中表达水平最低。
在第二个黑色的方框中,我们可以看到,这些基因在第1个样本中表达水平最高,而在第4个样本中表达水平最低。
在第三个橙色方框中中,我们可以看到,这些基因在第2个样本中的表达水平最高,而在第3个栖中的表达水平最低。
根据不同基因表达模式的相似性进行的“聚类”(clustering)并不是偶然的,而是通过一定的算法实现的,这些算法会将那些表达模式类似的基因放到一块,如下所示:
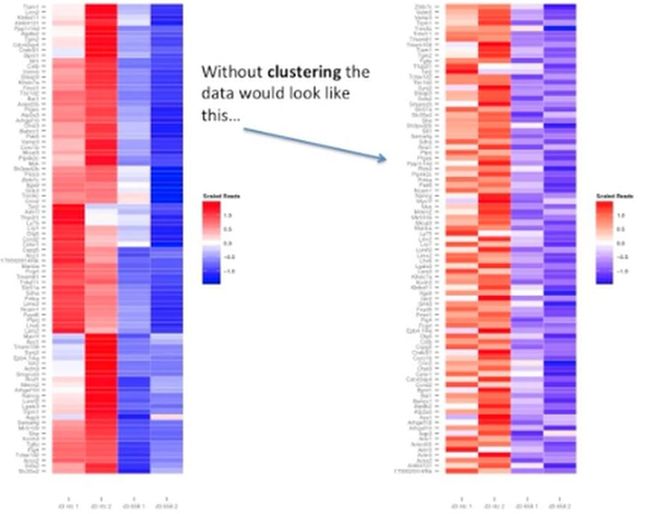
如果不进行聚类(clustering),那么用热图展示出来就是下图右边的那个样子,如下所示:
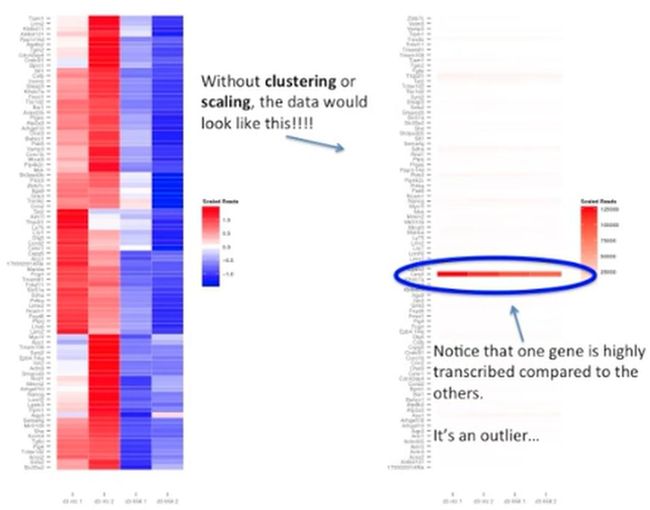
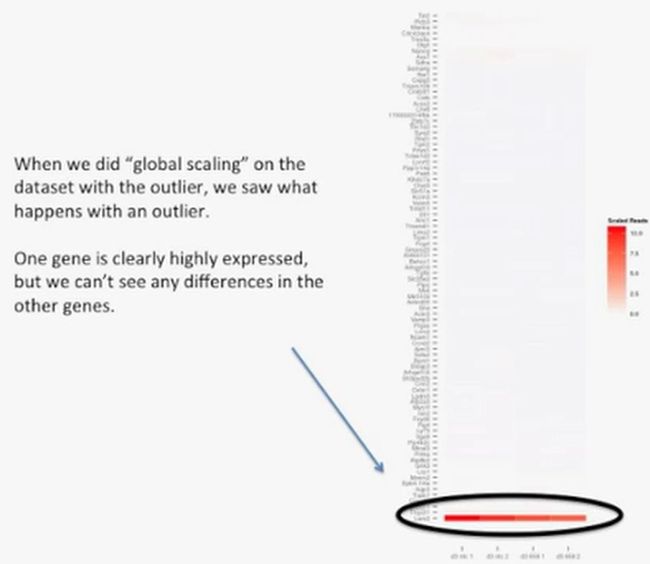
如果热图中既不进行聚类(clustering),也不进行缩放(scaling),那么热图就变成了如下的这个样子:
从图上我们可以看到,红色部分的这个基因表达水平最高(比其他的基因表达高太多了),可以把它视为一个异常值。
热图复杂案例
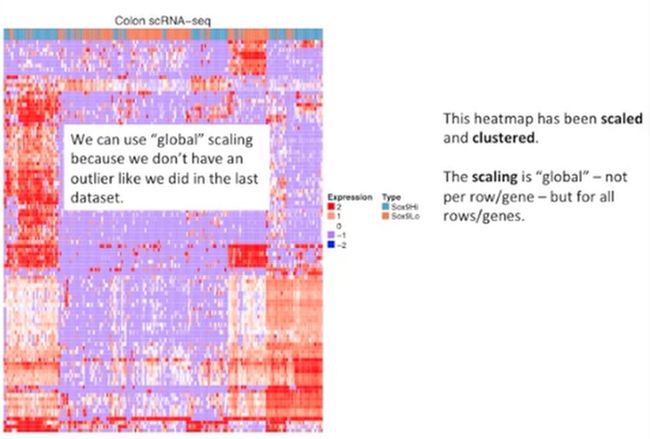
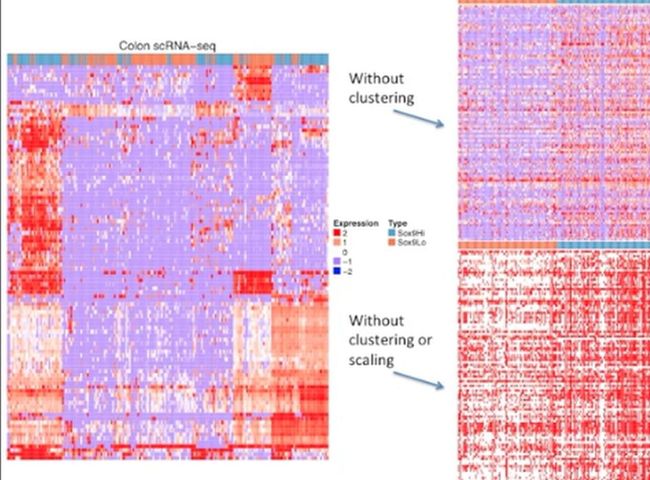
现在我们再看一下比较复杂的热图案例,如下所示:
从这个图的标题上我们可以看出,这个貌似是一个结肠的单细胞测序数据的热图。这个热图的数据经过了缩放(scaled)与聚类(clustered),它的缩放是全局的,因此,这一组数据中并没有异常值,这里的缩放要与前面热图的缩放区分开来,前面的前面是按照某个基因进行缩放的,也就是把同一行的数据当成整体,进行了缩放(也就是z转换),而这个数据是把所有的数据当作整体,进行缩放。
再看聚类。这个热图的聚类是按照列(column,也就是样本)和行(row,也就是基因)同时进行的聚类,如下所示:
在上图中,我们可以看到,纵矩形的部分表示基因表达模式相似的样本聚在了一起,横矩形表示的是,表达模式相似的基因聚集在了一起。它们的交集表示,这些样本的基因表达模式相似,以及有哪些基因相似。
如果不进行聚类,也不进行数据缩放(scaling),那么下图的右上表示的就是不聚类的热图,右下表示的就是即不进行聚类,又不进行缩放的热图,如下所示:
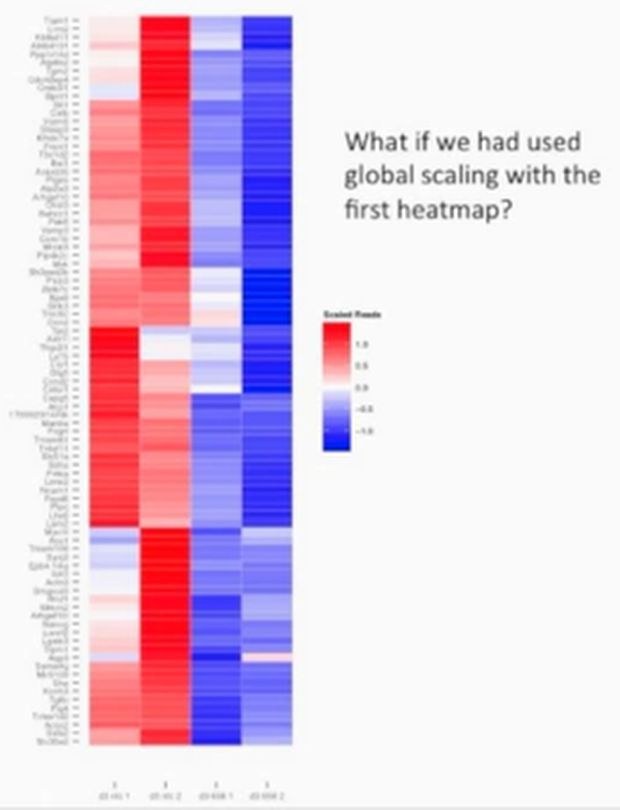
此时我们再回到前面的那个简单热图案例中来,我们试想一个问题,在那张热图中,如果我们对所有的基因进行整体的缩放(global scaling),而非单个基因的缩放,那么这个热图会怎么样,我们看下图:
经过全局缩放(global scaling)后,得到下面的图形,如下所示:
此时,我们会发现,这些聚类的结果就会发生了改变,并且新生成的图形中出面了异常高的热图,它是异常值,这个异常值会导致热图整体上出来严重的偏离,并且不容易观察基因的变化,如下所示:
因此,我们从上面的结果可以知道,缩放(scaling)会影响两个结果,第一,不同表达水平基因的颜色,这会影响你比较不同样本中的相同基因的表达水平,第二,影响聚类(clustering),如下所示:
如何对数据进行缩放(scale)
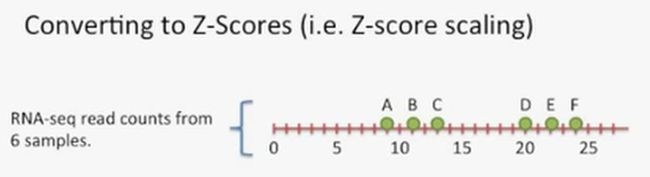
此时,我们再回到数据的缩放这个话题上,无论你对相同基因在不同样本中进行缩放,还是对全局的基因进行缩放,最常用的方法就是Z值缩放法(Z-Score Scaling),如下所示:
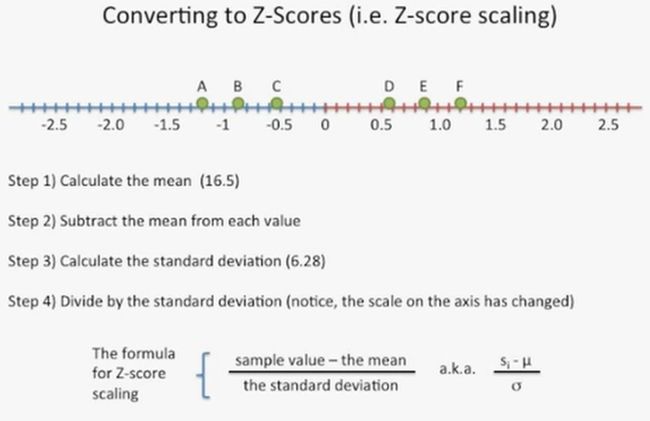
接着,我们具体看一下这种方法是如何实现数据的缩放的。在下图中,我们看到一个数轴上分布了几个样本的reads数,如下所示:
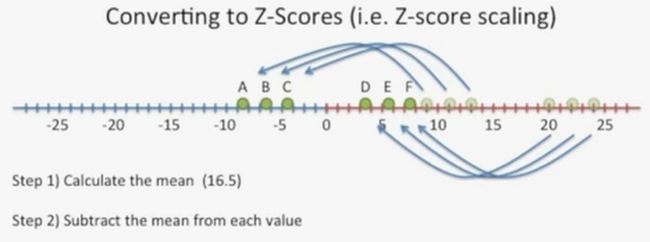
第一步:计算其均值(均值为16.5),如下所示:
第二步:每个样本的数值减去均值,此时,如果这个数值大,就表示此样本的某基因转录水平高;如果数值小,就表示此样本的某基因转录水平低,如下所示:
第三步:计算标准差(标准差为6.28);
第四步:将第2步中的数值除以标准差,如下所示:
经过上述的处理后,无论原始数据的变异程度如何,这些数据的范围最终会缩小,之所以这样处理,就是因为如果原始数据之间差异过大,那么不同基因表达水平就会变化程度(more subtle)更高的色度(shade)来表示,经过这样的处理,用较小程度的色度(shade)就能表示出基因水平的差异,方便观察,如下所示:
此时,我们可能会遇到这样的一种情况,例如,如果数据中出现异常值时,数据会怎么样,就像下面的这个样子:
此时如果进行Z转换的话,标准差会很大,也就是Z值的分子会很大,最终得到的值会有一部分集中在0附近,只能用很少的色度来进行区分,如下所示:
例如,我们如果采用全局缩放来处理原始数据中,在第一个案例中,我们就会得到下面这样的图形,其中有一个基因明显表达水平非常高,使得其它的基因差异很难看出来,如下所示:
如何聚类
原始数据经过缩放后(scaling),此时就可以进行聚类了,聚类有2种方法,分别是层次聚类(hierarchical clustering)和K-均值(K-means)聚类,我们先讲层次聚类(hierarchical clustering),如下所示:
层次聚类(hierarchical clustering)
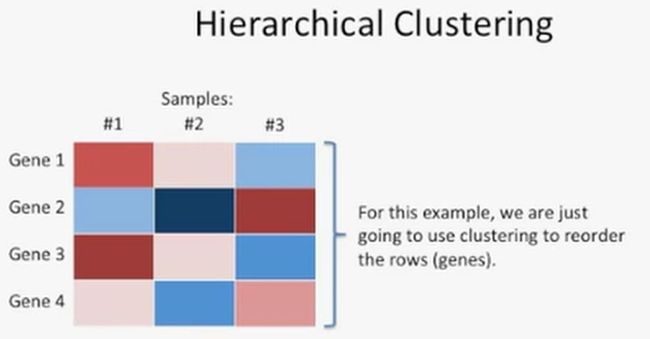
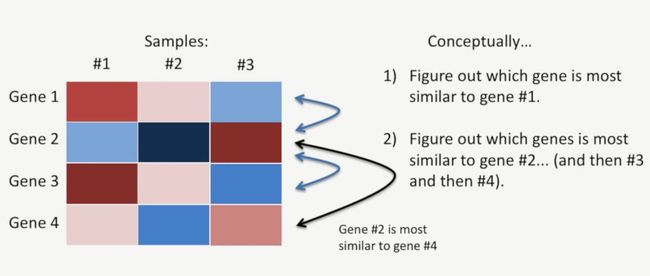
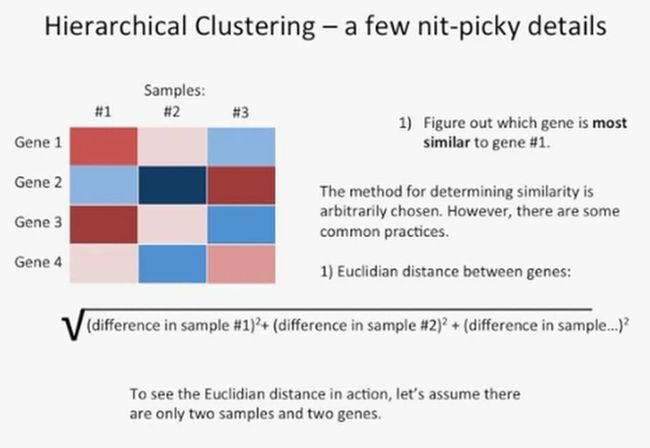
先看一个简单的案例,在这个案例中,有3个样本,每个样本4个基因,如下所示:
这种聚类方法的思路是这样的:
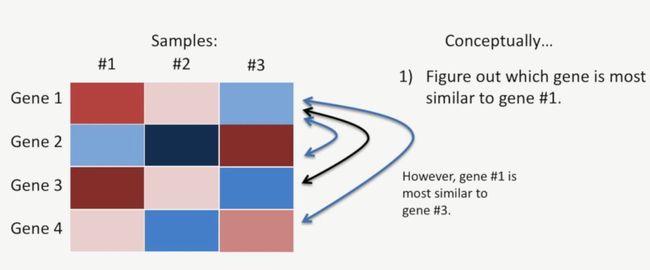
第一步,计算出哪些基因与基因1最为接近,基因2明显与基因1表达模式不同,基因3与基因1的表达形式比较类似,基因4与基因1的表达模式也比较类似,但是,在这几个基因中,与基因1表达模式最接近的还是基因3,如下所示:
第二步,计算出哪些基因的表达模式与基因2最为接近(然后是基因3,基因4),经计算发现,基因4与基因2的表达模式最相似,如下所示:
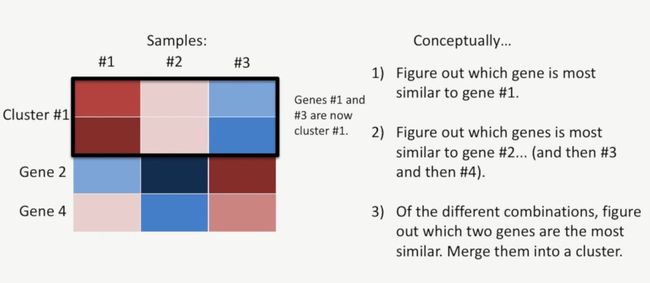
第三步,我们在前面找到基因1和基因3的表达模式相似,基因2和基因4的表达模式相似,但是,基因1和基因3的相似程度要比基因2和基因4的相似程度高,我们把前面的组合(基因1和基因3)放到一个簇(cluster)中,如下所示:
第四步:此时再回到第一步,把基因1和基因3构成的簇(Cluster # 1)当作一个基因,然后再按照第二步,第三步来计算,经计算,此时,基因2和基因4最相似,把它们再放到一个簇中(Cluster #2),如下所示:
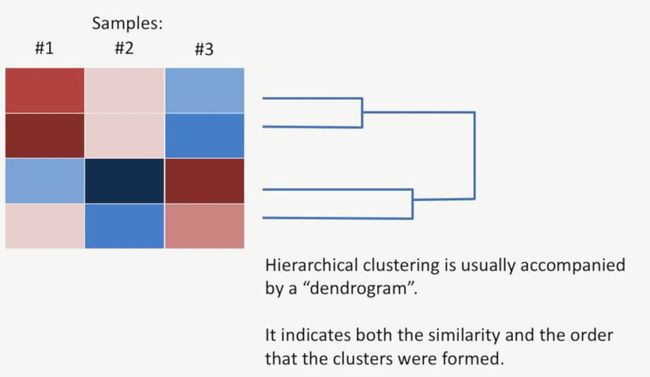
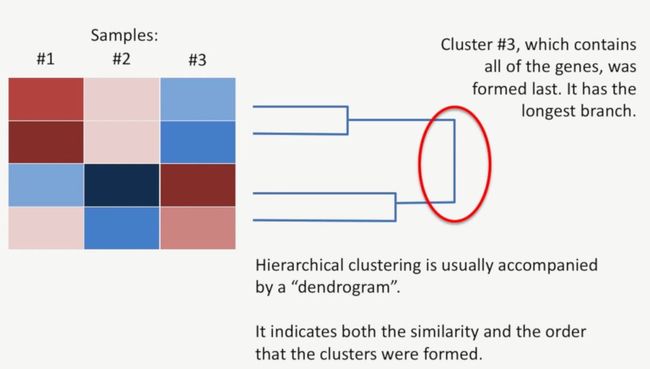
通常情况下,层次聚类(Hierarchical Clustering)通常会用一个树形图(dendrogram)连接起来,用于表明聚类成员之间的相似性和聚类次序,如下所示:
在右侧的树形中,我们可以发现,Cluster #1是最先形成的聚类,它们的相似性最高,如下所示:
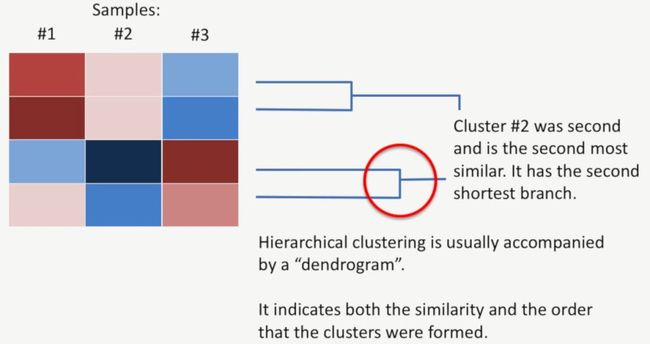
Cluster #2是第二个形成的聚类,它们的相似性次高,如下所示:
而第三个聚类Cluster #3则包含了所有的基因,它是最后形成的,如下所示:
层次聚类的原理
前面我们提到过,层次聚类的第一步就是计算两组基因的相似性,此时我们详细介绍一下如何进行计算。
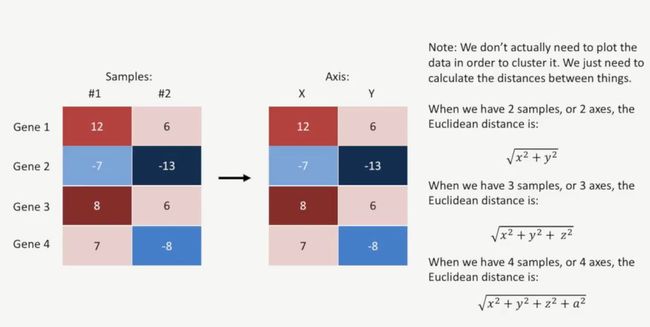
在计算相似性方面并没有一个统计的标准,但有一些常用的手段。第一种计算相似性的方法就是欧氏距离(Euclidian distance),如下所示:
为了简单地说明欧氏距离(Euclidian distance),我们以最简单的例子来说明,在这个例子中,有2个样本,每个样本有2个基因,然后两个样本的相同基因的差值的平方相加,并开平方,得到的数值就是欧氏距离,如下所示:
除了欧氏距离可以计算相似性外,还可以使用曼哈顿距离(Manhattan distance)和坎贝拉距离(Canberra distance)来计算相似性,其中曼哈顿距离只是不同样本之间相同基因差值的绝对值之和,如下所示:
我们看一下用不同的方法计算相似性的区别,下图的左侧图使用的欧氏距离(Euclidian distance)来得到的热图,右图使用的是曼哈顿距离(Manhattan distance)得到的热图,如下所示:
从图上来看,使用这两种不同的相似性计算方法得到的热图略有差异,具体要使用哪种方法来计算相似性,并没有一个统计的标准,它们也没有什么生物学意义。
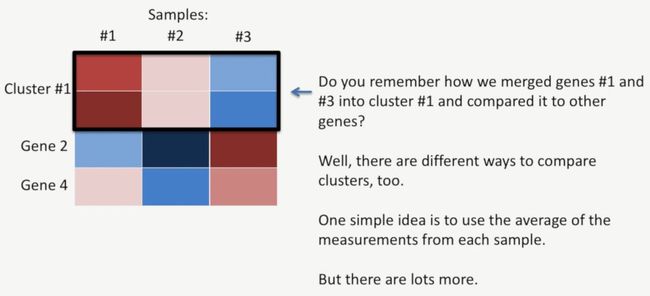
此时,我们再回到原来的案例中来,在前面部分中我们提到,基因1和基因3的相似程度最高,把它们都放到一个簇(Cluster #1)中,此时,我们如何计算Cluster #1和基因2,基因4的相似性呢?有几种方法。
其中最简单的一种方法就是求出Cluster #1中的两个基因的平均值,然后进行计算。但还有其它的方法,这些方法同样会影响聚类,如下所示:
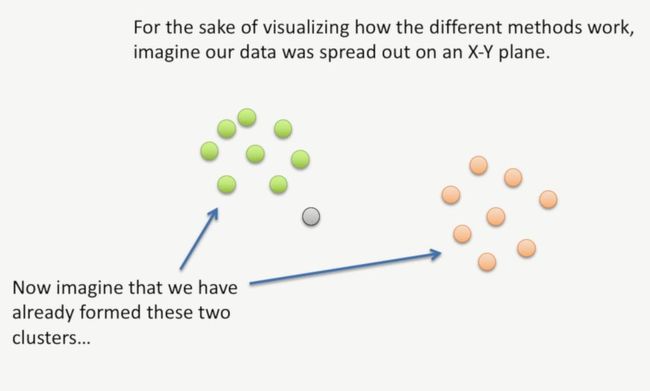
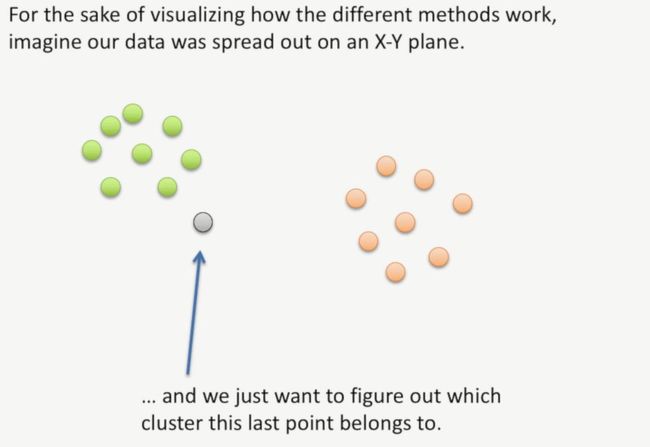
为了简单地说明簇(Cluster #1)与其它基因相似性计算的问题,我们假设有一批数据,分布在X-Y轴上,此时,我们已经生成了2个簇,如下所示:
此时,我们仅需要计算最后一个点属于哪个簇,如下所示:
此时我们可以采用以下这些方法进行计算:
第一,计算这个点与两个簇平均值的距离(centroid),如下所示:
第二,计算这个点到两个簇最近的点的距离(single-linkage),如下所示:
第三,计算这个点到两个簇中最远的点的距离(complete-linkage),如下所示:
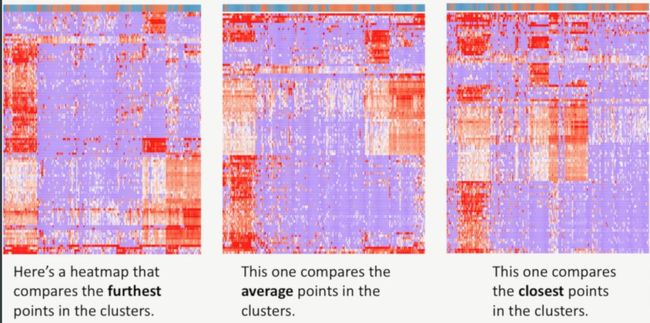
我们用前面的单细胞测序的热图来说明一下这三种方法,从左到右分别是:某点到某簇最远点的距离(在R中默认的就是这个选项),某点到某簇均值的距离,某点到某簇最近的点的距离,如下所示:
K-means聚类
什么是K-means
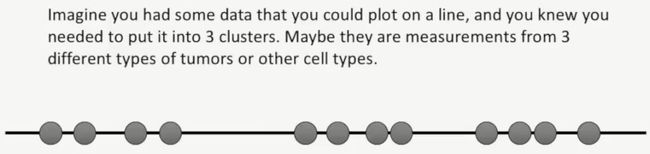
先看一个场景,例如我们手中有这样的一批数据,把它们绘制到一个数轴上,此时你的目的就是把它们分成3个簇(cluster),这三个数据或许是来源于三种不同的细胞或都是三种不同的肿瘤,如下所示:
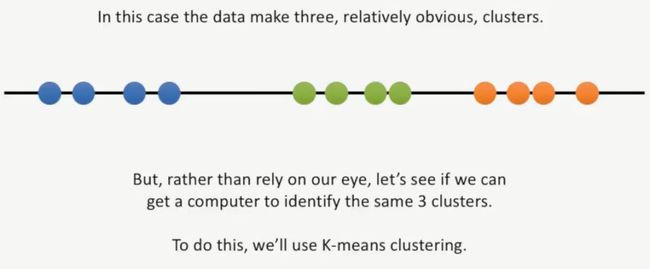
我们仅从肉眼观察,就知道这一批数据明显可以分成3个簇,但是,如果我们不用肉眼来观察,用计算机来计算,如何得到这3个簇呢?此时就需要用到一种算法,即K-means聚类,如下所示:
K-means的基本思想
此时,我们先了解一下K-means聚类的基本思想。
第一步:选择你要聚类的个数,K-means聚类中的这个K就是你要聚类的数目的意思,此时,你们选择K=3,这也就是说,我们想把这些数据取成3个簇(cluster),对这个K值如何选择,我们后文会提到,如下所示:
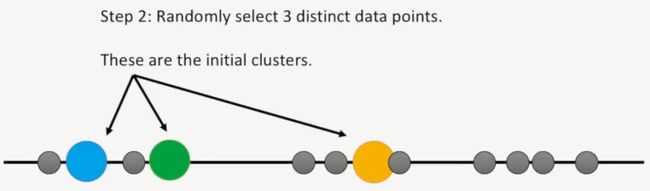
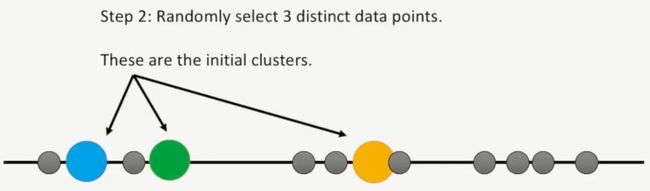
第二步,随机选择3个不同的数据点当成3个簇,如下所示:
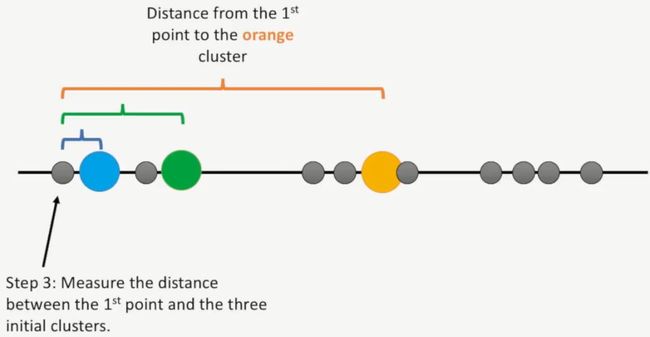
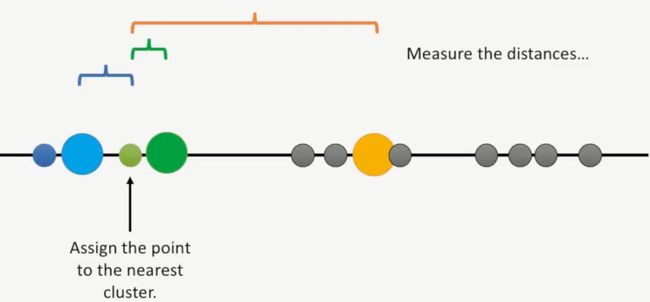
第三步:计算第1个点到这三个簇的距离,先计算第1个点到蓝簇的距离,如下所示:
接着,计算第1个点到绿簇的距离,如下所示:
最后,计算第1个点到橘黄簇的距离,如下所示:
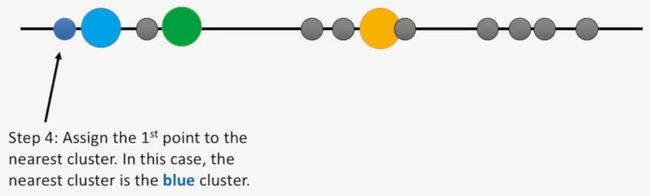
第四步:将第1个点归于离它最近的簇,在这个案例中,第1个点就属于蓝簇,如下所示:
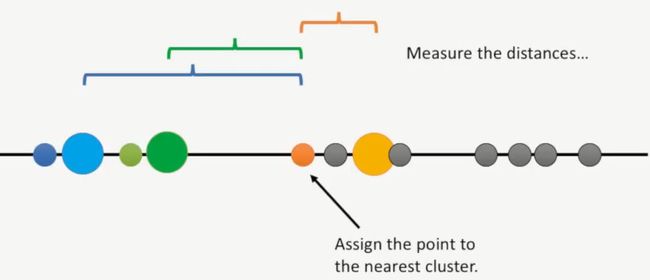
接着,重复前面的步骤,只是这次计算的第2个点,第2个点最终的计算结果它属于绿簇,如下所示:
再计算第3个点,它属于橘黄簇,如下所示:
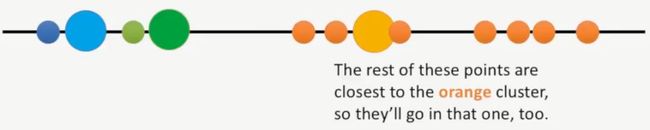
经过最终计算,第3个点到最后的点都属于橘黄簇,如下所示:
此时,所有的点都进行了聚类,如下所示:
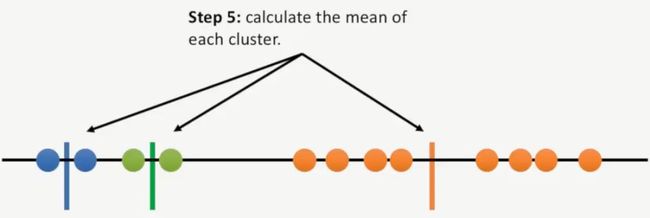
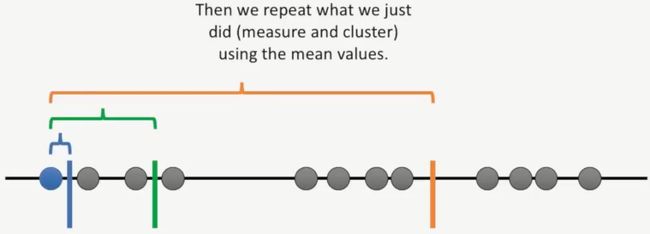
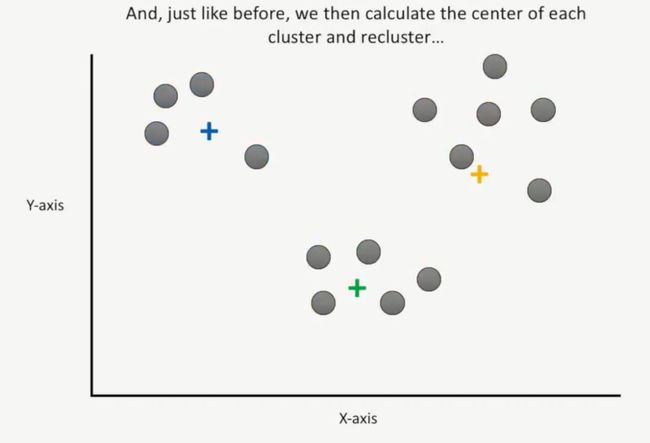
第五步:计算每个簇的均值,如下所示:
此时,我们还按照前面的方法,计算每个点到这三个簇的均值的距离,如下所示:
最终计算结果如下所示:
经过最终的计算,我们发现,这些聚类结果并没有发生改变,如下所示:
也就是说,K-means的聚类结果似乎比我们肉眼进行的聚类的结果还要差,如下所示:
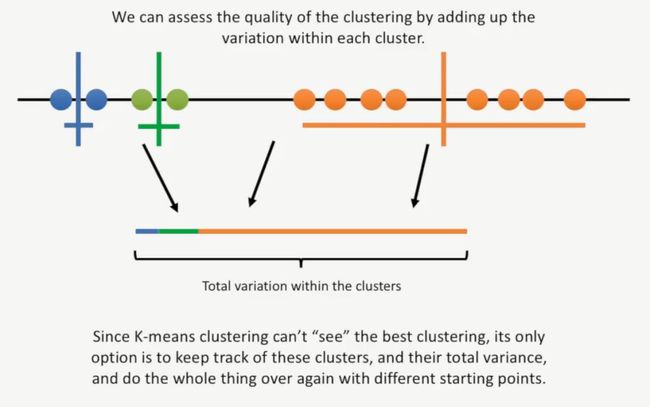
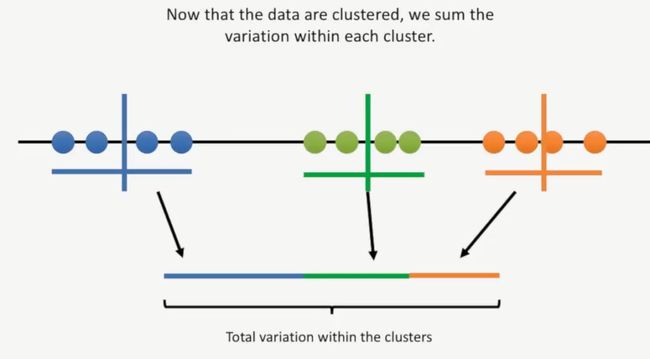
此时,我们需要对聚类的结果进行评估,其方法就是计算每个簇的变异,如下所示:
由于K-means的聚类过程并不能“看”到最佳的聚类,只能追踪这些簇与这些簇的总变异,然后通过不断更改起始的数据点进行迭代。
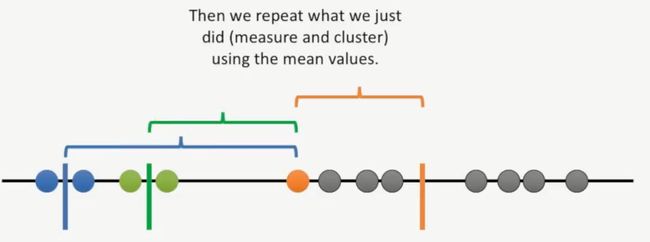
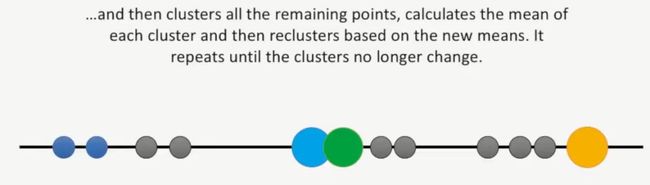
此时我们回到起点,再将随机选择3个初始数据点作为初始的簇,按照前面同样的自救,计算剩余的点到这三个簇的距离,计算每个簇的均值,然后基于新的均值进行聚类,直接这些簇不再改变为止,如下所示:
计算的结果如下所示,此时这些数据已经进行了聚类,再计算这三个簇的变异,如下所示:
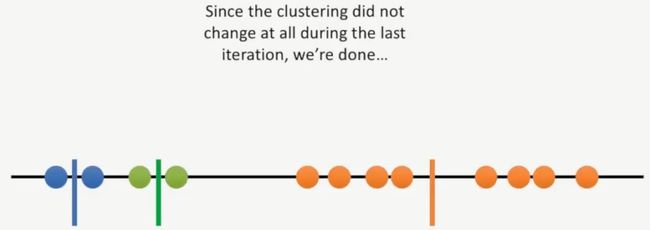
这一轮迭代结束,然后再来一轮,如下所示:
我们把这三次的聚类结果放一块儿,我们可以发现,第二次的聚类结果最好,如下所示:
但是我们并不清楚这个结果是不是所有可能的聚类结果中最好的(总变异最小),因此我们需要进行更多次的聚类,然后才能下结论。
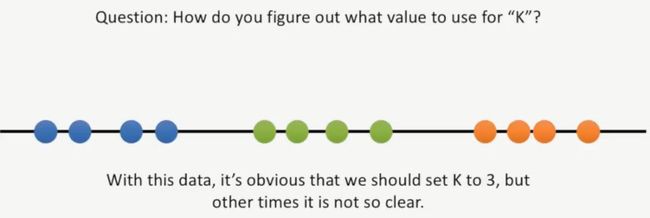
此时我们提出一个问题,K值应该如何选?在这个案例中,明显可以知道K值为3,但是,有的时候,这个K值并不像本案例中这么明显,如下所示:
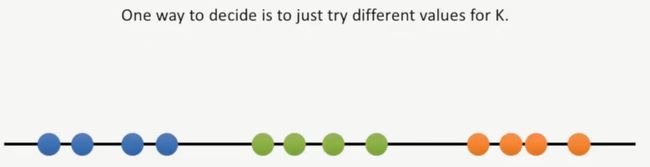
其中一种确定K值的方法就是不断地使用不同的K值,如下所示:
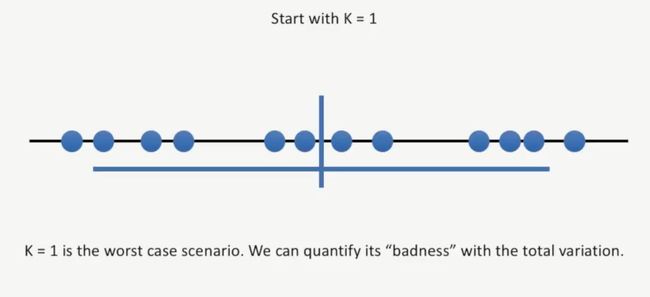
我们先使用K=1这个数值,通过计算总的变异程度,明显这个结果不行,如下所示:
再使用K=2,此时我们计算一下总变异,这个结果比K=1的时候要好一些,如下所示:
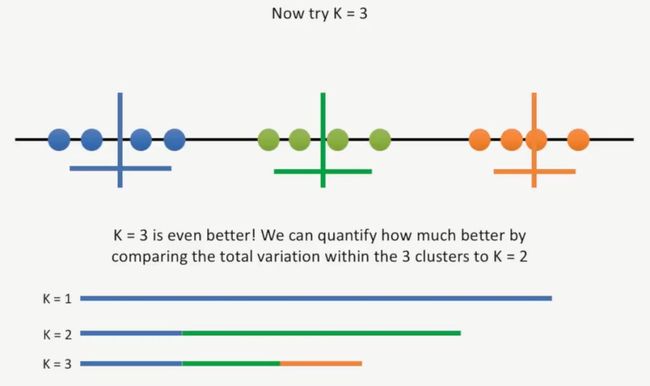
接着,我们使用K=3,通过计算它的总变异,我们发现K=3的结果要比K=2更好,因为它的总变异更低,如下所示:
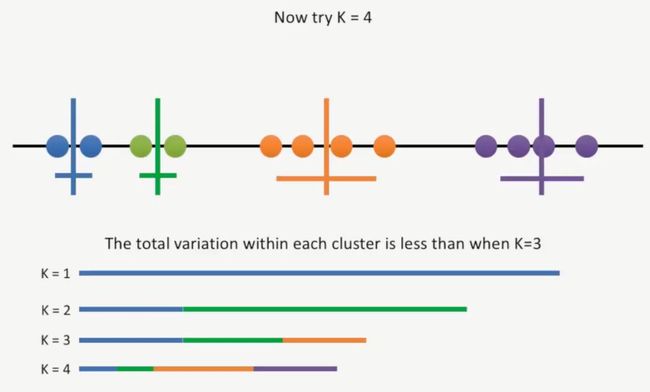
再继续,使K=4,我们发现,K=4的总变异比K=3的总变异还要小,如下所示:
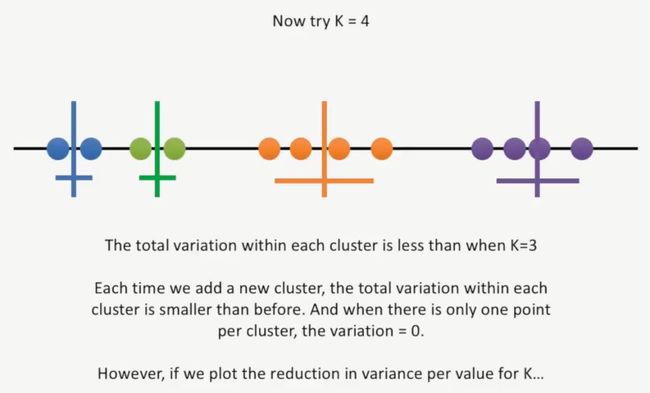
从前面的这些计算结果来看,我们能总结出一个规律,每当我们添加一个新的簇时,总变异就会降低,当簇的数目等于总的数据点的数目时,总变异就是0,如下所示:
如果我们把K值与变异降低的程度绘制成曲线,那么就能得到下面的这条曲线:
从这个曲线上我们可以看到,当K=3时,它之后的K值每增加1,总变异的降低幅度就没有前面的快,我们把K=3这个点称为拐点(elbow plot)。
K-mean聚类与层次聚类的区别
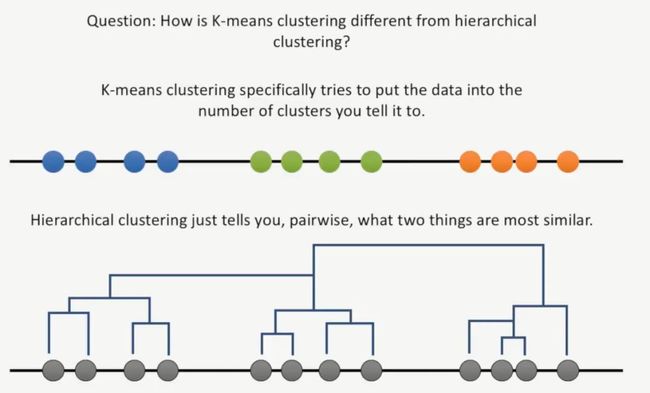
此时,我们再提出一个问题:K-mean聚类与层次聚类有什么区别?
K-means聚类会把数据聚成你所期望的簇的数目,而层次聚类则中介告诉你,哪两个数据是最相似的,如下所示:
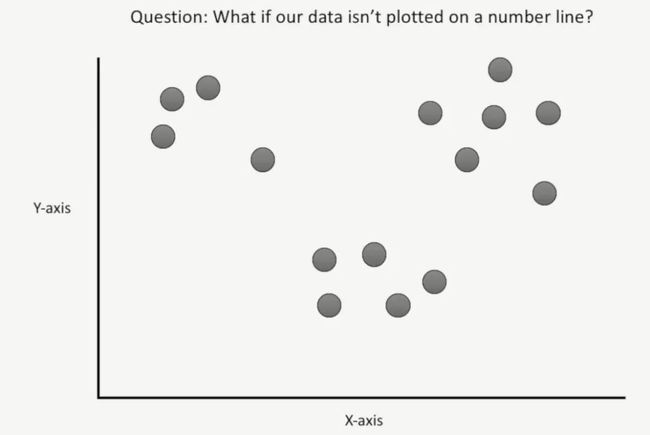
二维坐标的K-means
如果我们的数据无法绘制到一条数轴上时,如何进行K-means聚类呢,如下所示:
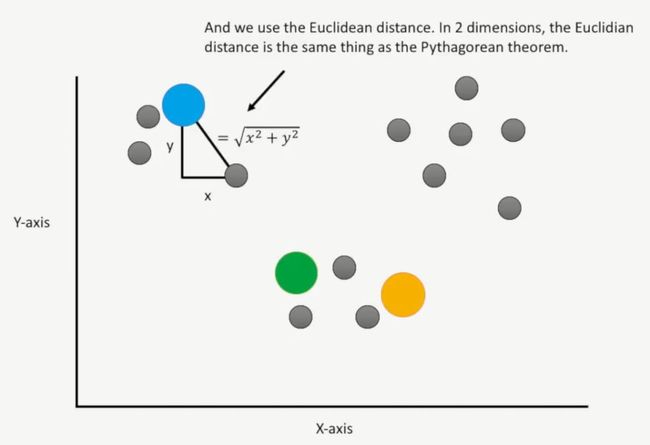
这种情况下,它的聚类原理跟一维数轴的原理一样,第一步就是随机找到三个点(前提是你想聚成3个簇),如下所示:
然后,计算不同的点到这三个簇的欧氏距离(Euclidean distance),在二维坐标中,计算这个欧氏距离就是采用勾股定理,如下所示:
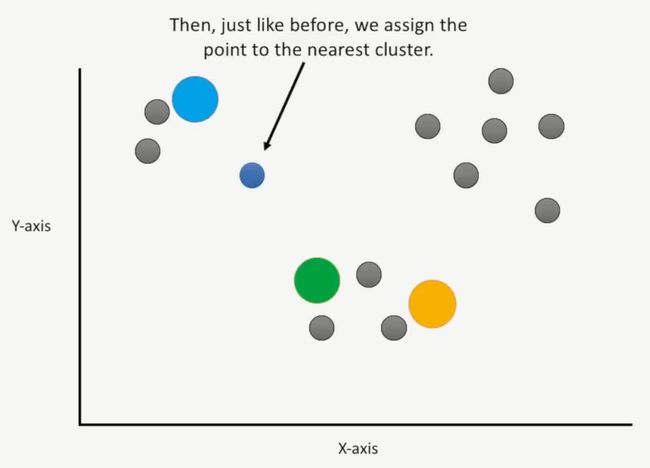
接着,就像前面讲的那样,距离最近的就属于某个簇,如下所示:
第一次的聚类结果如下所示:
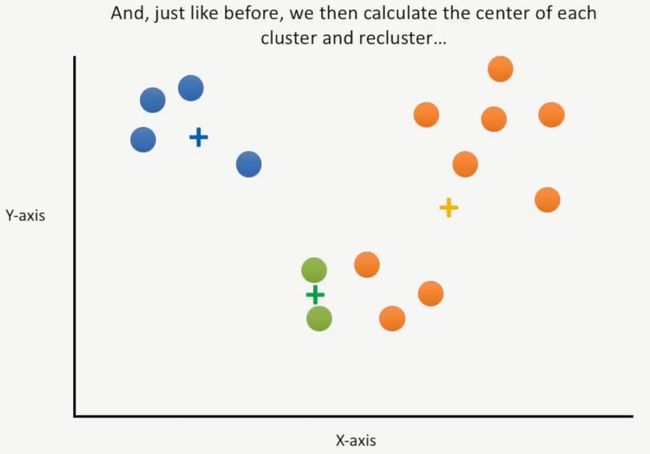
再接着,我们会像前面是找到的那样,计算出每个族的中心点(也就是均值),然后再聚类,如下所示:
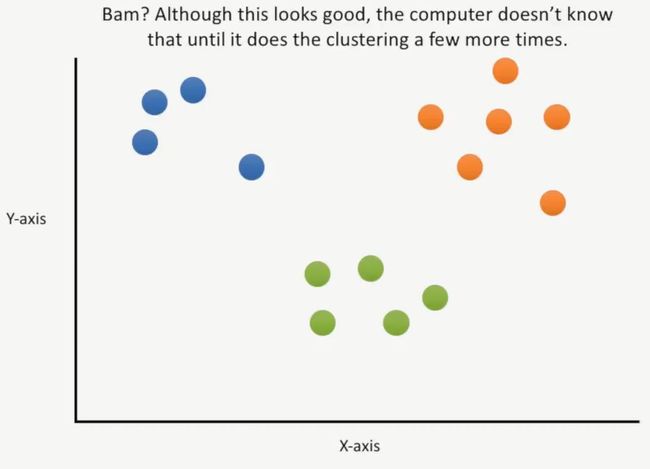
最后,得到比较满意的聚类图,如下所示:
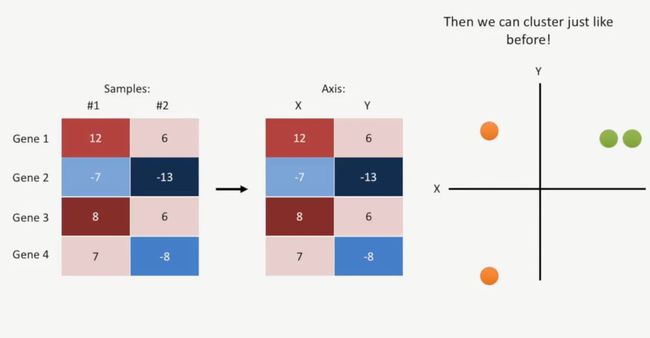
热图的K-means
如果我们的数据是热图,那么如何进行K-means聚类呢?
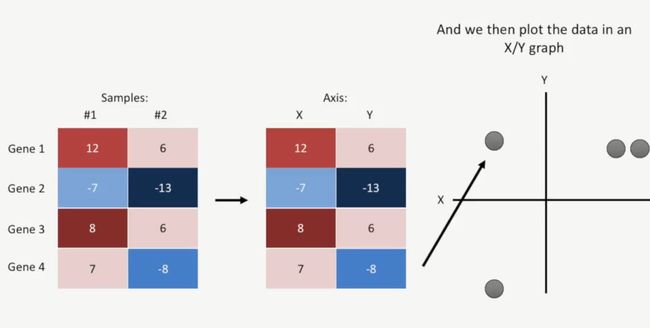
为了方便描述,我们就以下面的案例说明一下,两个样本(sample 1和sample 2),分别有4个基因,现在把这两个样本分别命令为X,Y,把它们的基因放到二维坐标轴上,如下所示:
然后像前面那样进行聚类,如下所示:
事实上,在实际的计算过程中,我们并不需要把数据投射到二维坐标上,只用计算不同样本之间的距离即可,例如欧氏距离,如下所示:
R的kmeans()函数备注
在R中,进行K-menas聚类的函数是kmeans(),它有一些注意事项。
- 此函数会对每个距离加上权重,因此那些大簇(large clusters)的权重要略高于小簇(small clusters)的权重。
- 默认情况下,此函数只有一组原始的簇,如果你要使用多个不同的起始数据点,那么你需要设定参数
nclust=25或者是25左右的数字,例如(kmans(data, k=3, nclust=25))。
如下所示: