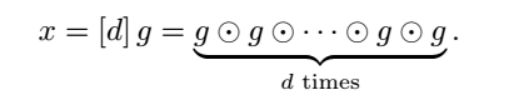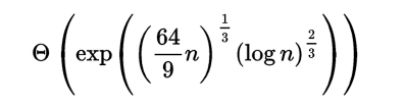关于Quantum Algorithms for Computing Short Discrete Logarithms and Factoring RSA Integers阅读报告
关于《用于计算短离散对数和因式分解RSA整数的量子算法》阅读报告
一、文章主要思想与工作
文章主要思想是通过概括量子算法和描述用于计算短离散对数的算法的应用,从而改进了用于计算短离散对数和因式分解RSA整数的量子算法,使算法更为简单及方便。
本文作者主要工作是推广本文中的量子算法来计算短离散对数,进一步将指数的大小减少到略大于m位。此外文章根据对短离散对数的算法,RSA整数的因式分解,以及在边信息下寻找组的顺序,可能会被重建为短离散对数问题产生一个算法来分解RSA整数,比shor算法在量子计算机上要求简单更多。
二、相关技术
1、计算离散对数问题
所谓离散对数,就是给定正整数x,y,n,求出正整数k(如果存在的话),使y≡xk(mod n)。就目前而言,人们还没有找到计算离散对数的快速算法(所谓快速算法,是指其计算复杂性在多项式范围内的算法,即O(logn)k,其中k为常数)。虽然有快速计算离散对数的量子算法,其计算复杂性为O(logn)2+?着,但现在并没有量子计算机(实用的量子计算机也许根本就建造不出来)。
而离散对数的应用是离散对数公钥加密算法,其安全性要远远高于基于大数分解的RSA算法。方法如下:
公钥密码体制的运作过程(假定A和B两个人要在一个不安全通道如因特网上形成密钥以备日后加密解密所用)。首先,A、B两人要共同公开约定一个素数q和有限域Fq中的一个生成元g;A选定一个随机数a∈{1,2,…,q-1}(a可以认为是A之私钥),并将g a(modq)传送给B;B选定一个随机数b∈{1,2,…,q-1}(b可以认为是B之私钥),并将gb(modq)传送给A;此时A可以算出(g b)a(modq),B也可以算出(g a)b(modq),由于(gb)a(modq) = (g a)b(modq) = g ab(modq),因此,A和B就形成了一个公共的密钥g ab(modq),日后便可以此钥来进行传统的加密解密计算,从而达到在不安全的通道上进行保密通讯的目的。
显然,敌方可以截获到g,q,g a(modq),g b(modq)。因此,如果敌方有快速的求解离散对数的算法,就能从已截获的上述信息中迅速求出a或b,从而算出g ab(modq)。遗憾的是,目前世界上根本就没有快速的求解离散对数的算法,因此当所选的有限域Fq很大时,a或b就很难算出。
离散对数形式相对比较灵活,每个发送端可以在发送每条消息是指定自己的公钥,但接收端回复的消息也只有发送端才能解密;也可通信握手阶段协商密钥,接下来根据协商的密钥走对称加密。
资料来源:https://en.wikipedia.org/wiki/Discrete_logarithm
http://blog.csdn.net/chen77716/article/details/7106485
2、因式分解RSA整数
所谓因式分解,即给出两个大约数,很容易就能将它们两个相乘。但是,给出它们的乘积,找出它们的因子就显得不是那么容易了。这就是许多现代密码系统的关键所在。如果能够找到解决整数分解问题的快速方法,几个重要的密码系统将会被攻破,包括RSA公钥算法和Blum Blum Shub随机数发生器。
尽管快速分解是攻破这些系统的方法之一,仍然会有其它的不涉及到分解的其它方法。所以情形完全可能变成这样:整数分解问题仍然是非常困难,这些密码系统却是能够很快攻破。有的密码系统则能提供更强的保证:如果这些密码系统被快速破解(即能够以多项式时间复杂度破解),则可以利用破解这些系统的算法来快速地(以多项式时间复杂度)分解整数。换句话说,破解这样的密码系统不会比整数分解更容易。这样的密码系统包括Rabin密码系统(RSA的一个变体)以及Blum Blum Shub随机数发生器。
而RSA的安全性依赖于大数分解,但是否等同于大数分解一直未能得到理论上的证明,因为没有证明破解RSA就一定需要作大数分解。假设存在一种无须分解大数的算法,那它肯定可以修改成为大数分解算法。RSA的一些变种算法已被证明等价于大数分解。不管怎样,分解n是最显然的攻击方法。人们已能分解多个十进制位的大素数。因此,模数n必须选大一些,因具体适用情况而定。
RSA算法是一种非对称密码算法,所谓非对称,就是指该算法需要一对密钥,使用其中一个加密,则需要用另一个才能解密。RSA的算法涉及三个参数,n、e1、e2。其中,n是两个大质数p、q的积,n的二进制表示时所占用的位数,就是所谓的密钥长度。e1和e2是一对相关的值,e1可以任意取,但要求e1与(p-1)*(q-1)互质;再选择e2,要求(e2×e1)≡1(mod(p-1)×(q-1))。n,e1),(n,e2)就是密钥对。其中(n,e1)为公钥,(n,e2)为私钥。RSA加解密的算法完全相同,设A为明文,B为密文,则:A≡B^e2( mod n);B≡A^e1 (mod n);(公钥加密体制中,一般用公钥加密,私钥解密),e1和e2可以互换使用,即:A≡B^e1 (mod n);B≡A^e2( mod n)。
RSA的公钥、私钥均有接收端(比如Server)签发,非常适合互联网上的证书服务:服务端签发证书,客户端使用该证书,保证客户端到服务端之间的通信安全。如果双端都需要非对称加密,则双方都必须发布公钥,并且公钥不能频繁变更,做不到每个端点一个公钥,因此,任何一个接收端都可以查看发送端的消息(公钥解密)。
资料来源:https://en.wikipedia.org/wiki/RSA_Factoring_Challenge
https://en.wikipedia.org/wiki/RSA_(cryptosystem)
https://en.wikipedia.org/wiki/Integer_factorization
3、量子算法及量子计算机
量子分解算法利用量子计算的并行性,可以快速分解出大数的质因子,将使量子计算机很容易破解目前广泛使用的密码如RSA公钥加密系统,严重威胁到银行、网络和电子商务等的信息安全以及国家安全。因此,Shor算法的提出迅速引起了世界各国对量子计算研究的高度关注。
而量子计算机(quantum computer)是一类遵循量子力学规律进行高速数学和逻辑运算、存储及处理量子信息的物理装置。当某个装置处理和计算的是量子信息,运行的是量子算法时,它就是量子计算机。
量子计算机在密码破解上有着巨大潜力,当今主流的非对称(公钥)加密算法,如RSA加密算法,大多数都是基于于大整数的因式分解或者有限域上的离散指数的计算这两个数学难题。他们的破解难度也就依赖于解决这些问题的效率。传统计算机上,要求解这两个数学难题,花费时间为指数时间(即破解时间随着公钥长度的增长以指数级增长),这在实际应用中是无法接受的。而为量子计算机量身定做的秀尔算法可以在多项式时间内(即破解时间随着公钥长度的增长以k次方的速度增长,其中k为与公钥长度无关的常数)进行整数因式分解或者离散对数计算,从而为RSA、离散对数加密算法的破解提供可能。但其它不是基于这两个数学问题的公钥加密算法,比如椭圆曲线加密算法,量子计算机还无法进行有效破解 。
资料来源:https://en.wikipedia.org/wiki/Quantum_computing
三、文章的算法
sage代码
RSA加密解密过程:
# randomly select some prime numbers
p = random_prime ( 1000 ) ; p 191
q = random_prime ( 1000 ) ; q 601
# compute the modulus
N = p * q
R = IntegerModRing ( N )
Phi_N = ( p-1 ) * ( q-1 )
# we can choose the encrypt key to be anything
# relatively prime to Phi_N
e = 17
gcd ( d , phi_N ) 1
# the decrypt key is the multiplicative inverse
# of d mod phi_N
d = xgcd ( d , phi_N ) [1] % phi_N
d 60353
# now we will encrypt/decrypt some random 7 digit numbers
P = randint ( 1 , 127 ) ; P 97
# encrypt
C = R ( P ) ^ e ; C 46685
# decrypt
R ( C ) ^ d 97
P = randint ( 1 , 127 ) ; P 46
# encrypt
C = R ( P ) ^ e ; C 75843
# decrypt
R ( C ) ^ d 46
P = randint ( 1 , 127 ) ; P 3
# encrypt
C = R ( P ) ^ e ; C 288
# decrypt
R ( C ) ^ d 3
对大整数进行运算:
p = random_prime ( 1000000000 ) ; p 114750751
q = random_prime ( 1000000000 ) ; q 8916569
N = p * q
R = IntegerModRing ( N )
Phi_N = ( p-1 ) * ( q-1 )
e = 2 ^ 16 + 1
d = xgcd ( d , phi_N ) [1] % phi_N
d 237510735093473
P = randint ( 1 , 1000000 ) ; P 955802
C = R ( P ) ^ e
R ( C ) ^ d 955802
四、未来的研究方向、未解决的难题等
目前的难题是量子算法不够精良,不够方便应用。未来的研究方向还要继续优化量子算法,例如用于分解一般整数的shor算法,把一个随机群元素取幂到一个长度为l+ m位的指数,其中元素的阶数r范围或限制条件是r <2m和l = m / s,量子算法被执行多次后,以整数j1,j2,...的形式产生部分结果,最后就像
类似。也要在L里面寻求一个非0的整数r,可以使算法更为方便和简单的运行。
最重要的方向还是在优化算法后,制造出真正意义上的量子计算机,破解算法,量子数值计算,量子系统的模拟等等好多复杂的问题将会迎刃而解。