给定一个二维数组,它的行和列都是已经按升序排列,请设计一个算法,对于给定某个值x,判断该值是否包含在数组中。例如给定一个二维数组如下:
A = {
{2, 4, 6, 8 , 10},
{12, 14, 16, 18, 20},
{22, 24, 26, 28, 30},
{32, 34, 36, 38, 40},
{42, 44, 46, 48, 50},
}
如果给定的x值是34,那么算法返回该值所在的行和列,也就是3和2,如果x的值是35,那么算法返回该值不存在。
在我们以前的算法讨论中曾经提到过一个法则,当看到有数组时,首先想到的就是排序。如果看到排序,首先想到的是二分查找,对于给定数组,它已经排好序了,那么我们可以考虑用二分查找来判断给定元素是否在数组中。
我们先看最简单的做法,最简单的莫过于一个个查看,也就是算法遍历每一个元素,看看是否与给定数值相等。这种做法算法复杂度是O(n*n)。
第二种做法就是使用二分查找,由于每一行都是升序排列的,那么我们可以对应于一行,先用二分查找法,探寻给定元素是否在某一行,如果不再这行,那么我们选择新一行,再次使用二分查找去检测给定元素是否存在给定行。第二种做法效率比第一种要高,因为二分查找的复杂度是lg(n),因此算法的复杂度是O(n*lg(n))。
我们能否更进一步,找到更好的算法呢?题目给定的特征是,数组的行和列都是升序排序的,第二种做法只利用了行是升序排列这一性质,对于列的升序排列并未利用到,如果能够利用到这一特性的话,那么我们就可以设计出更高效的算法,由此我们得到第三种算法如下,假设数组的长度为n:
1, 用x与A[0][n-1]比较,如果 x < A[0][n-1], 那根据数组每一列都是升序排序的特性,我们可以排除掉数组的最后一列。
2, 如果x > A[0][n-1], 那么根据数组每一行按照升序排列的特性,我们就可以排除掉数组的第0行。
3, 如果x == A[0][n-1], 算法直接返回。
4, 如果算法查询的行数超过n,或者列数小于0,那表明数组不包含给定元素。
根据上述算法描述,我们给出算法的代码实现如下:
public class TwoDArraySearch {
private int[][] searchArray;
private int seachValue;
private int row = 0;
private int col = 0;
public int getRow () {
return this.row;
}
public int getCol () {
return this.col;
}
public TwoDArraySearch(int[][] array, int val) {
this.searchArray = array;
this.seachValue = val;
this.col = array[0].length - 1;
}
boolean search() {
while (this.row < this.searchArray[0].length && this.col >= 0) {
if (this.searchArray[this.row][this.col] == this.seachValue) {
return true;
}
if (this.seachValue > this.searchArray[this.row][this.col]) {
this.row++;
}else if (this.seachValue < this.searchArray[this.row][this.col]) {
this.col--;
}
}
return false;
}
}
在程序的主入口中,我们设计数据如下:
import java.util.AbstractMap;
import java.util.AbstractMap.SimpleEntry;
import java.util.Arrays;
import java.util.Map.Entry;
import java.util.Random;
public class Search {
public static void main(String[] args) {
int[][] array = {
{2, 4, 6, 8 , 10},
{12, 14, 16, 18, 20},
{22, 24, 26, 28, 30},
{32, 34, 36, 38, 40},
{42, 44, 46, 48, 50},
};
TwoDArraySearch s = new TwoDArraySearch(array, 34);
if (s.search() == true) {
System.out.println("Array contains element which is in row " + s.getRow() + " and in col " + s.getCol());
} else {
System.out.println("Array does not contain the given element");
}
}
}
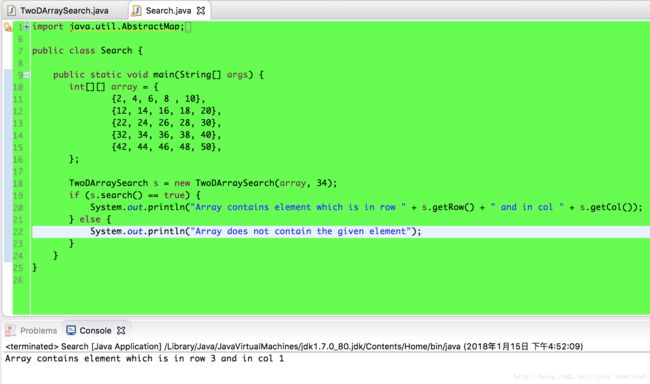
代码先构造了一个行和列都按照升序排列的数组,并设置要查询的数值为34,显然该值包含在数组中,然后调用TwoDArraySearch 的search()函数,上面代码运行后结果如下:
根据输出结果,我们可以判断,算法的实现是正确的。
我们再看看算法的复杂度,根据算法步骤描述,每当执行步骤1或2时,算法都会排除掉一行或者一列的元素,这意味着,算法要检测的元素数量减少了n个,一个n*n的数组,它只有n行和n列,也就是说,步骤1和2最多只能执行n次,因此第三种算法的复杂度是O(n)。
更详细的讲解和代码调试演示过程,请点击链接
更多技术信息,包括操作系统,编译器,面试算法,机器学习,人工智能,请关照我的公众号: