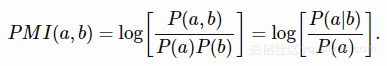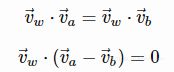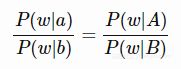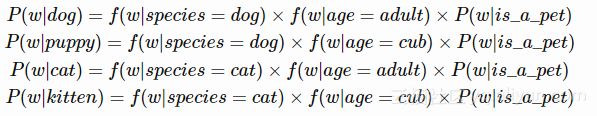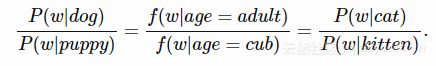介绍
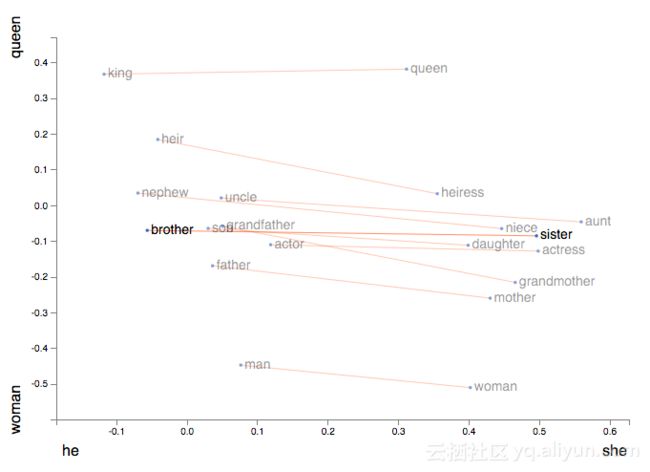
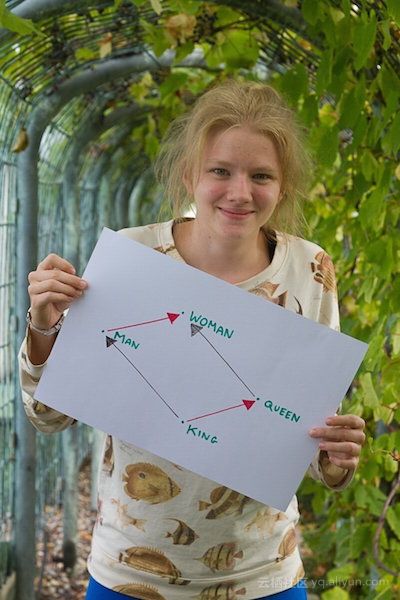
word2vec是将单词转换为向量的算法,该算法使得具有相似含义的单词表示为相互靠近的向量。此外,它能让我们使用向量算法来处理类比,例如着名等式 king - man + woman = queen
本文我将尝试解释它的工作原理,并且会特别强调向量差异的意义,同时尽量避免过于技术层面的细节。
如果你希望自己探索这方面的内容,这里是我学生Julia Bazińska的互动探索,她现在是华沙大学计算机科学的一名新生:
计数,巧合和含义
有时一个看似简单的方法却能给出了意想不到的结果。 事实证明,仅仅从单词组合,而不是所有的语法和语境,可以提供我们获知一个单词的意义。 让我们看看这句话:
A small, fluffy roosety climbed a tree.
什么是roosety? 我会说,像松鼠(squirrel)一样的小动物,因为这两个词可以很容易互换。 这种推理称为分布假设,可以归纳为:
理解一个词要看它的结伴关系 - 约翰·鲁伯特·弗斯
如果我们要训练计算机,最简单的方法就是让它只识别单词对。令 P(a|b) 为单词b在给定间隔内,存在单词a的条件概率(假设给定间隔不超过2个单词)。如果对于每个单词w都有
P(w|a)=P(w|b)
然后我们就能说单词a与b相似。换句话说,如果我们有了这个等式,不管是否有单词a或b,所有其他单词都以相同的频率出现。
即使简单的单词数统计,比较文本的出处,我们可以得到有趣的结果。例如: 金属乐的歌词中的单词统计(“哭泣”,“永恒”或“灰烬”是非常常见的,而“特别”或“大致”则不是),见重金属音乐和自然语言处理(Heavy Metal and Natural Language Processing)。
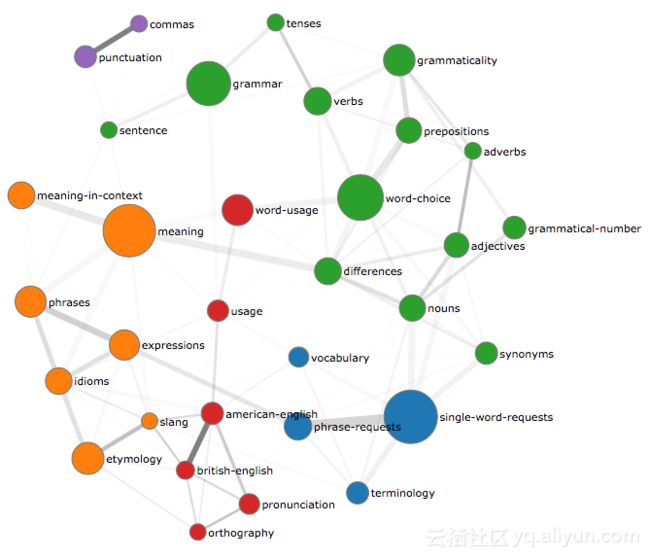
查看单词共同出现的现象可以给我们提供很多的信息。 例如,我的一个项目,TagOverflow,其目的是只基于Stack Overflow的标签来发现程序的结构。 其中,我的关注点在于点互信息(PMI)的研究,这也引出了我们下一个话题。
点互信息和压缩技术
压缩器:将认知视为压缩。 压缩感知,近似矩阵分解 – 机器学习中的文化
原则上,我们可以计算每个词对的P(a|b) 。 但是即使只有一个10万单词量的小词典(记住,我们需要保留所有单词的偏差,正确被使用的单词和那些虽然不在官方的字典中,但正在使用中的单词)跟踪其所有的单词对,我们就需要8千兆字节的空间。
为此我们通常不使用条件概率,而是点互信息(PMI),其定义为:
它的直接解释是,我们得到一个单词对的概率要比随机得到他们要高出多少。 对数使得更容易处理以不同数量级的频率出现的词。 我们可以将PMI近似为标量积:
其中维的向量。
一开始你可能会好奇,所有的单词竟然可以被压缩到一个更小维度的空间。 其实有一些单词是可以被互换(例如John->Peter)的,并且一般有很多类似的结构。
事实上,这种有损压缩可能也会有它自己的优势,因为我们通过这样方式可能会发现某种模式,而不只是记住每个单词对。 例如,在用于电影评级的推荐系统中,每个评级就是两个向量(电影的内容和用户的偏好)标量积的近似值。 这种方法可以用于预测尚未看到的电影的分数,请参阅使用TensorFlow的矩阵因子分解 - Katherine Bailey。
单词相似性和矢量接近性
让我们从简单的开始 - 显示向量空间中的单词相似性。 条件 P(w|a) = P(w|b) 等效于
PMI(w,a)=PMI(w,b)
通过等式两边除以 P(w) 并取对数。 那么用向量表示PMI后,我们就得到了
如果我们需要它作用于每个
,则就有了
也就是说,它强调给定词与其他单词共存的方向,而不是这种效应的强度。
类比和线性空间
如果我们想要进行单词比较(由a得到b,是因为由A得到B),可以认为对于每个词w,我们有条件概率比的等式
当然,该等式看起来像(其实就是)一个有问题的假设,但它仍然是我们可以用条件概率达到的最佳结果。 我不会试图为这个方法辩护,但我会使用一些与其等同的其他方式。
例如,如果dog(狗) 之于puppy (小狗),就像cat (猫)之于 kitten(小猫),我们就会期望如果dog(狗)和cat(猫)有着紧密的共生关系(可能出现频率不一),那么puppy(小狗)和kitten(小猫)也有着同样的共生因素。
通过提出词类比的比率,我们隐含地假设单词的出现概率可以相对于单词不同维度的因式分解。 对于上面的例子,那就是:
条件概率比的等式如何转换为单词向量? 我们将它改写为互信息(同上取P(w)对数)
就等同于
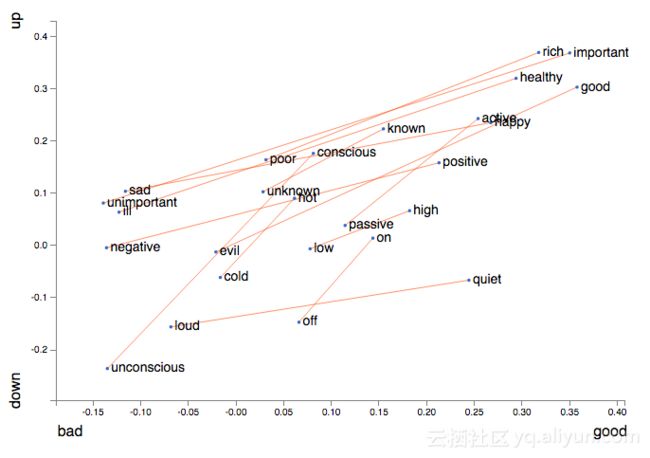
同时,如果我们希望它作用于任意单词w,这个向量差需要为零。可以使用类比来表示单词意思(如用向量改变性别),语法(如改变时态)或其他类比(如城市与其邮政编码)。 似乎类比不仅是单方面的技巧 - 我们可能可以一直使用它们来考虑问题,详见:
向量差和向量投影
词向量的差,就比如
并不是词向量本身。 然而,有趣的是在坐标轴上词向量的投影。 我们可以看到其投影
就是一个单词在不同上下文中的相对出现。
记住,当我们想看一个单词的常见方面时,更平均两个向量而不是取其总和是更自然的。 虽然人们可以互换使用它,它只工作,因为余弦距离忽略绝对向量长度。 所以,对于一个性别中立的代词使用
而不是他们的和。详见Word Spectrum 和 Word Associations 这两个项目
一起来试试!
如果你想亲手探索一下词向量,我推荐可以先看看JuliaBazińska的Word2viz。 你可以在几个预定义图中进行选择,或从头开始(选择单词和其投影)。 同时我也注意到谷歌研究也发布了一个类似工具:可视化高维数据的工具 - 谷歌研究博客(和其演示版本:嵌入投影机)。
如果要使用预训练向量,请参阅Stanford GloVe或Google word2vec的相关文档。 以及正在开发的样例github.com/lamyiowce/word2viz。
如果你想在自己的数据集里进行训练,那就用Python的gensim库:人类主题建模。 通常需要一些预处理,特别是看看Matthew Honnibal的Sense2vec与spaCy和Gensim。
如果你想从头开始,最方便的方法是从Vector Representations of Words - TensorFlow Tutorial开始。
如果你想了解更多词向量是如何工作的,我推荐以下资料:
一个词相当于一千个向量 作者:Chris Moody
Daniel Jurafsky, James H. Martin 的 语言和语言处理 (2015):
第15章: 向量语义 (Vector Semantics)
第16章: 语义与密集向量(Semantics with Dense Vectors)
技术
这里我解释了把单词转换成向量的算法。 每个方法都需要更多的调整。 以下是一些技术方面的解释:
word2vec不是单一的算法
虽然单词和上下文本质上是相同的(两者都是由单词组成),但需要区别对待它们(考虑不同的单词频率)
有两类词向量(每个单词有两个向量,一个用于单词,另一个用于上下文)
因为任何实际的数据集将包含一些单词组PMI,在大多数情况下,我们使用正点互信息(Positive PMI)
通常需要预处理(例如,捕捉诸如机器学习的短语,或者区分具有两个单独含义的单词)
意义线性空间是一个有争议的概念
所有结果都是基于我们输入的数据而计算得到的,并不是客观事实; 所以很容易得到一些奇怪的结果,比如:doctor - man + woman = nurse.
如需进一步的阅读,我建议以下参考资料:
· How does word2vec work? 作者: Omer Levy
· Neural Word Embeddings as Implicit Matrix Factorization, 作者: Omer Levy
· Skipgram isn’t Matrix Factorisation作者:Benjamin Wilson
· Language bias and black sheep
· Language necessarily contains human biases, and so will machines trained on language corpora 作者:Arvind Narayanan
· Word Embeddings: Explaining their properties作者:Sanjeev Arora
· Issues in evaluating semantic spaces using word analogies,作者:Tal Linzen,
背景故事
我在word2vec和相关技术领域的研究:
•矩阵分解,
•点互信息,
•概念隐喻,
•模仿人类认知的简单技术。
感谢
本文受益于Grzegorz Uriasz和Sarah Martin的相关研究。 我想特别感谢Levy Omer关于指向词向量算法的弱点(和阴影假设)的研究成果。
以上为译文
本文由阿里云云栖社区组织翻译。
文章原标题《king - man + woman is queen; but why?》,译者:friday_012