ROC分析

算法工作中，经常要对模型进行评估，由此衍生出很多指标。比如Accuracy、Precision、Recall、F1-score、AUC等等。准确理解各指标的内涵、使用场景及局限，还挺有挑战。更佳阅读体验，请移步ROC分析。

论文《An introduction to ROC analysis》对常见指标进行了较细致的分析，且重点放在ROC曲线以及周边概念上，非常经典。

涉及问题及指标较多，采用逐个点梳理的方式比较助于理解。

简单例子

以经典的二分类问题为例。某个分类器，可将样本分为正类或负类，样本本身是正类或负类，如此

样本有两类标签

预测标签
真实标签

交叉后对应四种情况

True Positive: 正类被正确分类为正类
False Negative: 正类被错误分类为负类
True Negative: 负类被正确分类为负类
False Negative: 负类被错误分类为正类

当有多个样本时候，对上述四种情况汇总，可以得到2x2的混淆矩阵。

上述四种情况中，命名有规律

True表示预测正确；False表示预测错误；再根据Positive或Negative作逻辑运算，知道真实类别是Positive或Negative。

则有

true positive: positive表示被预测为positive，且true，真实是positive
false negative: negative表示被预测为negative，且false，真实是positive
true negative: negative表示被预测为negative，且true，真实是negative
false positive: positive表示被预测为positive，且false，真实是negative

混淆矩阵及常见指标

多个样本分布在上述四种情况下，形成混淆矩阵，由此可以计算各种各样的指标。

algo-confusion-matrix

上图为论文中配图，其中

p/n表示真实标签正/负
Y/N表示预测标签正/负
P/N表示真实正/负样本大小
TP/FP/FN/TN分别表示四种情况样本大小

常见指标如下

tp rate = TP/P 真阳率，又叫recall或者hit rate等，正确分类正样本占所有正样本比例
fp rate = FP/N 假阳率，又叫false alarm rate等，表示错误分类负样本占总负样本比例
recall = TP/P 同真阳率
precision = TP/(TP + FP) 表示正确分类正样本占分类为正样本的比例
accuracy = (TP + TN)/(P + N) 不管正负，表示正确分类样本占所有样本比例
F-score = 2/(1/precision + 1/recall) 是recall和precision的调和平均

注意，其中tp rate只用到正样本，fp rate只用到负样本，他指标正负样本都会用到。ROC曲线根据fp rate和tp rate绘制，由于单独只用到正或负样本，后续可看到ROC曲线对正负样本不均衡不敏感，这是很好的性质。

此外注意混淆矩阵四个区域并非等大小，如图手绘部分

正方样本非均衡，混淆矩阵两列非等宽
l1位置控制tp rate；l2控制fp rate
虚线l1越往下tp rate越高(好)；虚线l2越往上fp rate越高(坏)
l1往下移(好)，多数情况l2也会往下移(坏)；l2往上移(好)，多数情况下l1也会上移(坏)；其方向倾向一致，但一好一坏
总之两个值会互相伤害，需要一个trade off

ROC曲线

ROC graphs are two-dimensional graphs in which tp rate is plotted on the Y axis and fp rate is plotted on the X axis. An ROC graph depicts relative tradeoﬀs between beneﬁts (true positives) and costs (false positives).

分类器分两种

Discrete Classiﬁer
- 只输出正或负类
Probabilistic Classiﬁer
- 输出为正类的概率
- 未矫正得分，分数越高，正类概率越大

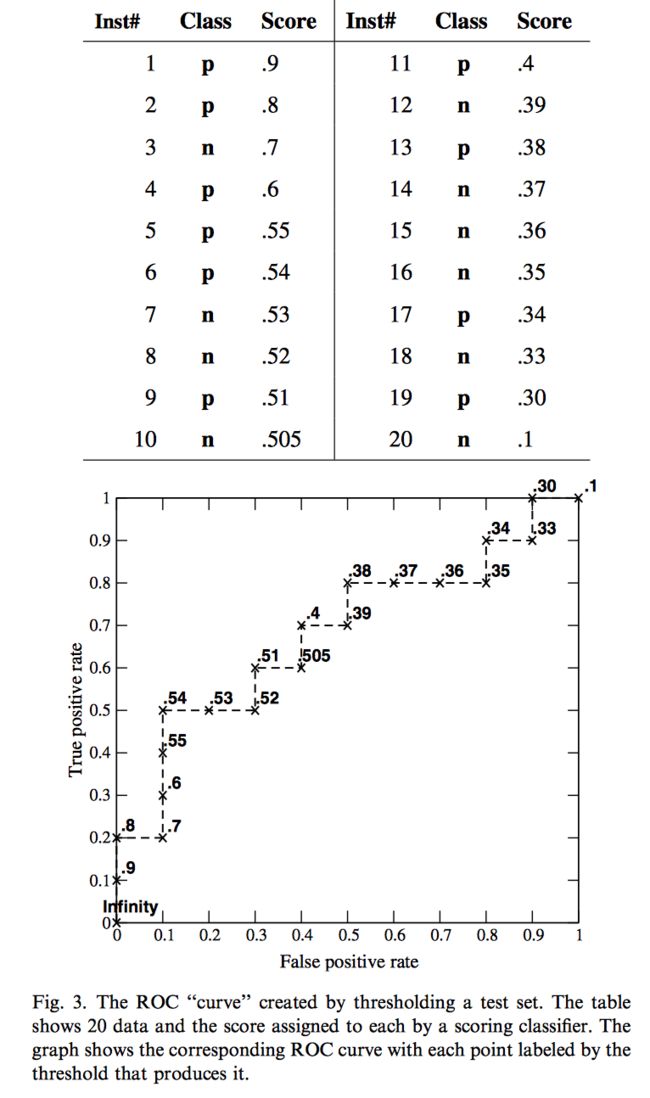
在一份测试集上，Discrete Classiﬁer只得到ROC曲线上一个离散点，如图中的A、B、C等点；

algo-roc-1

Probabilistic Classiﬁer则不同，通过取不同阈值，可得到ROC曲线上一系列点，形成一个step function。

algo-roc-2

四个特殊点

ROC曲线上有四个坐标点比较特殊：

(0,0)所有样本预测为负样本；不会有负样本误判为正样本，假阳率为0；不会有正样本被召回，真阳率为0
(1,1)所有样本预测为正样本；所有负样本都误判为正样本，假阳率为1；所有正样本都被召回，真阳率为1
(0,1)完美分类器；没有负样本被误判为正样本，假阳率为0；所有正样本都被召回，真阳率为1
(1,0)颠倒分类器；所有负样本均误判为正样本，假阳率为1；所有正样本未被召回，真阳率为

大体上将，越接近左上角(0,1)，分类器性越倾向于好。一个非正式解释就是

越靠左，分类器越conservative，证据很强时，才分类为正样本，fp rate较低
越靠右上侧，分类器越liberal，证据不太强时，就分类为正样本，fp rate较高

对角线

对角线上的点表示以固定概率随机猜测的分类器。比如对任何样本，均以20%概率猜测其为正类，则tp rate为0.2，因为每个正样本只有20%的机会被召回；同样fp rate为0.2，因为每个负样本都有20%的概率被判为正样本。

(0.5,0.5)随机猜测，一半一半，一半正样本能正确分类TPR=0.5，一半负样本被错误分类FPR=0.5
(0.2,0.2)随机20%猜测正类，有20%的正样本正确分类TPR=0.2，一半负样本被错误分类FPR=0.2
(0.8,0.8)随机80%猜测正类，有80%的正样本正确分类TPR=0.8，一半负样本被错误分类FPR=0.8

由于随机猜测分类器的ROC曲线是对角线y=x，所以任何学到信息的分类器，都会在对角线上方。当如果ROC曲线位于右下方时，分类器是学到信息的，但其用法不正确

A classiﬁer below the diagonal may be said to have useful information, but it is applying the information incorrectly.

只需要将其negate，即预测正类，将其看做负类，反之亦然。这样(0.4,0.2)=>(1-0.4,1-0.2)=>(0.6,0.8)，关于x=0.5和y=0.5两天直线对称过去即可。

分类器得分

大部分分类器会输出得分，相对分可以表示样本间的相对顺序；绝对分一般用来表示正样本的概率。

如果得分校准过，能很好地表示概率，则可直接卡阈值判断正负，accuracy等指标较好
如果不能很好表示概率，卡0.5阈值就会出现论文中Fig.4的矛盾，AUC=1但正确率确只有80%
得分能否能表示概率这一区分挺重要

An important point about ROC graphs is that they measure the ability of a classiﬁer to produce good relative instance scores... The ROC curve shows the ability of the classiﬁer to rank the positive instances relative to the negative instances, and it is indeed perfect in this ability.

ROC评估的是将正负样本正确排序的能力，强调的是序。

algo-roc-3

样本不均衡

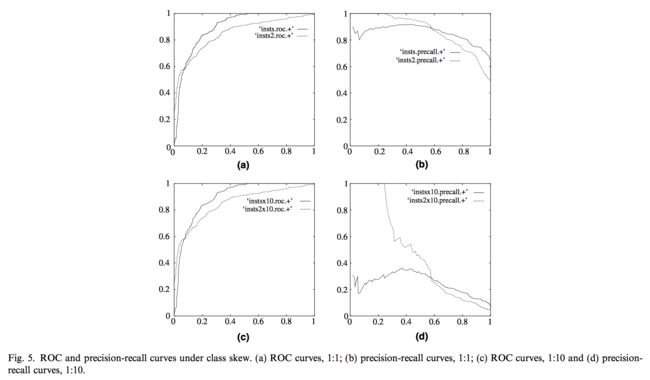
实际场景中，正负样本都很不均衡，如广告点击、风控领域等。ROC曲线一个重要特点就是对样本不均衡不敏感，样本分布剧烈变化，但ROC曲线变化很小。

如图当样本比例从1:1=>1:10时候，ROC曲线基本影响很小，但precision-racall曲线波动剧烈。

algo-roc-4

因为tp rate和fp rate都只用到正样本或负样本，都是简单的columnar ratio。而其他指标都会用到正样本或负样本。

ROC绘制

ROC曲线生成比较简单，将所有样本按得分降序排列，挨个取样本的得分值作为阈值，得到一系列fp rate和tp rate值。每次处理一个新样本，增量更新fp rate和tp rate值，最终一遍线性扫描即可。

其算法复杂度主要在排序阶段O(nlog(n))，排序后线性扫描复杂度O(n)。

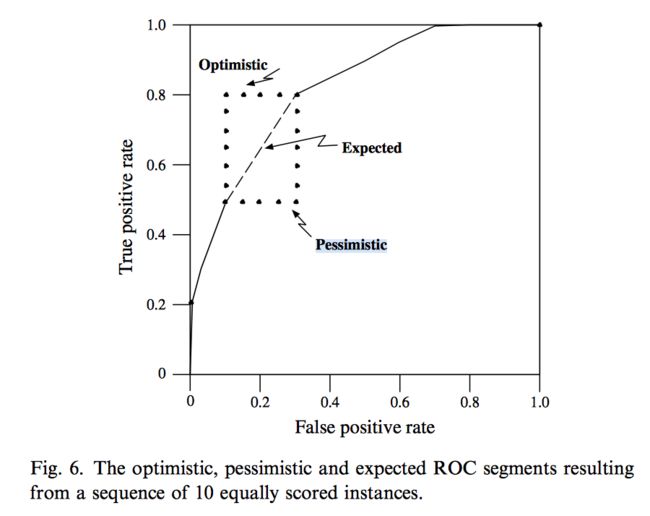
注意一点，实际会遇到多个正负样本得分相同的情况，此时要对optimistic和pessimistic做简单平均。

algo-roc-5

AUC含义

AUC是ROC曲线下面积，经常用来衡量排序模型效果，其含义是

The AUC has an important statistical property: the AUC of a classiﬁer is equivalent to the probability that the classiﬁer will rank a randomly chosen positive instance higher than a randomly chosen negative instance.

简单讲就是取一对(正, 负)样本，将正样本排在负样本前面的概率。

平均ROC

仅凭一个ROC评估模型优劣是有误导性的，因为未考虑到ROC本身的variance。

It is analogous to taking the maximum of a set of accuracy ﬁgures from a single test set. Without a measure of variance we cannot compare the classiﬁers.

比较稳健的是取多个测试集，生成多个ROC曲线，然后对其平均(vertical and threshold averaging)等，作为最终结果。