查尔斯·惠伦,美国达特茅斯大学教授,1997 到 2002 年间担任《经济学人》杂志驻美国中西部地区记者。主要从事经济学研究,曾在《芝加哥邮报》《纽约时报》和《华尔街日报》发表过多篇文章,所著《赤裸裸的经济学》是畅销多年的经济学普及读物。
关于本书
这是一本关于统计学常识的科普书,作者从理财投资、民意调查、医疗健康、刑事判决等生活案例中剥茧抽丝,向我们展示了妙趣横生的统计学规律。
核心内容
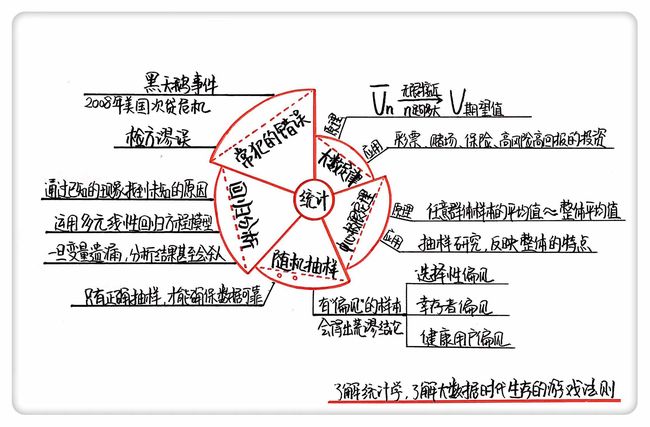
本书作者认为,作为大数据时代炙手可热的学问,统计学可以解决很多实际问题。可如果运用不当,统计学也会制造假象、造成误导。因此,我们很有必要掌握一些统计学中的概念和原理,它们并不艰涩难懂,却能帮我们读懂真相,预测未来。核心内容包含五个部分:1、大数定律;2、中心极限定理;3、随机抽样;4、回归分析;5、常犯的概率学错误。
一、大数定律
相同条件下,当随机试验次数足够多时,实验结果的平均值会无限接近 “期望值”。
1. 我们可以通过研究概率,明智地选择投资理财方式
【案例】就算是某期彩票爆出大奖掏空了奖池,从长远看,发行彩票也是稳赚不赔。根据“大数定律”,发行机构只要保证彩票的销售额大于奖金期望值,就肯定赚钱,所以沉溺于博彩是非常不理智的。
对于投资门槛高、风险大,但是回报很高的项目,如果把注意力都放在高回报率上很危险。大数定律成立的前提是“试验次数足够多”,如果你没有承担多次投资失败的资本,孤注一掷的投资很可能会血本无归。
2. 帮助我们理性面对风险
【案例】对小额电子产品推出的付费延保服务,商家肯定稳赚不赔,用户选择付费延保基本上等于浪费钱。但对于那些大额度人身、财产意外险,它们更多的是一个规避风险的理性工具,帮你在遭受一些难以承受的巨大损失时渡过难关。虽然保险公司赚取了巨大的利润,这种钱我们还必须得花。
二、中心极限定理
依据该定理,我们对一个基数庞大的群体做统计调查时,只要对其中的一部分样本进行研究,得出的结论就能反映整个群体的特点。
1. 如果掌握了某个群体的具体信息,就能推理出从这个群体中正确抽取随机样本的情况。
【案例】一个城市同时在举办马拉松比赛和吃热狗大赛,比赛前有一辆载满外国马拉松运动员的公交车失踪了,结果警察找到了一辆载满大胖子外国人的公交车。由于语言不通,警察只能根据经验判断:即使马拉松选手里面可能也有一两个略重的,但是满车都是胖子不大可能,因此很可能找错了车。
2. 如果已知两个样本的基本特性,就能推理出这两个样本是不是来自同一个群体。
【案例】上述案例中如果找到两辆车,乘客各自有胖有瘦,该怎么判断?这时候可以测量乘客体重,计算体重分布的标准差。根据中心极限定理,马拉松运动员群体的体重标准差是明显小于普通群体的,他们的体重分布更加集中于平均值周围。由此仍然可以判断出哪辆车是我们要找的。
三、随机抽样
这是收集数据的主要方法,核心是必须保证每个对象被抽到的概率完全相等。但大部分调查的对象是人群,人口组成非常复杂。如果不能保证等概率抽样,抽样数据就会存在“偏见”,就会得出错误结论。
1. 选择性偏见:样本选择带有潜在倾向性时就会出现。
【案例】1936年美国总统大选时,《文学文摘》杂志面向订阅者开展的民意测验,是史上知名度最高的统计错误。杂志编辑没有意识到,订阅这本杂志的人平均来说要比普通美国民众更富有,他们更倾向于投票给保护富人利益的共和党。这样带有选择性偏见的样本即使容量很大,也无法正确反映民意。
2. 幸存者偏见:如果样本中有数据缺失,会导致样本组成发生改变。
【案例】很多投资基金公司会同时开放20只新基金,经过三年的经营,总会有2到3只基金连续三年“跑赢”标准普尔指数。公司只要把十几只失败的基金悄悄关闭,大肆宣传这两三只“幸存者”,就可以把投资者的钱骗进来了。而实际上,这些“幸存”基金接下来的表现会逐渐回归平均水平。
3. 健康用户偏见:用来比对的样本其实选择在了不同群体当中。
【案例】假设卫生部门发现,哈佛大学新生中有98%的人在少年时期穿紫色睡衣,而监狱里的犯人中只有3%的人这样做过。因此得出了一个结论:穿紫色睡衣的孩子确实更有可能取得成功。这很显然是很荒谬的结论,这个问题在于我们用来对比的两组人根本就是两类人。真正对孩子大脑发育起作用的,是给孩子穿上紫色睡衣的家长,他们更注重对孩子的家庭教育。
四、回归分析
1. 对那些错综复杂的问题,回归分析可以通过建模计算,从已知现象中还原未知原因,甚至可以计算每种原因对结果的贡献比例。
【案例】医学家发现,级别较低的公务员更容易患上心脏病。 “白厅”研究项目组经过长时间纵向数据采集,比对了可能导致心脏病的一系列原因,包括低阶公务员的学历普遍偏低、烟民比例高、医疗服务差、加班多、锻炼少等等。面对这些错综复杂的变量,统计学家建立回归方程,计算了各个变量和心脏病发病率的线性关系。回归分析表明,造成心脏病高发的真正原因,是对工作缺乏控制力和话语权。而这类存在感较低的岗位,在低级别职位中更常见。
2. 电脑永远不能代替人的工作,如果在进行回归分析时遗漏了变量,就会得出危险的结论。
【案例】上世纪90年代,哈佛大学医学院对12万名女性开展纵向调查,经回归分析显示,定期摄入雌激素可以减少女性心脏病发病率,随后医院开始提供雌激素的补充治疗。而后来的临床试验发现,此举会导致乳腺癌和血栓病高发,因此死亡的女性患者可能达到上万人。
五、常犯的概率学错误
1. “黑天鹅”事件:忽视小概率事件,有时会造成严重的后果。
【案例】2008年美国次贷危机爆发前,整个北美金融行业都在使用同一个风险价值模型来预测投资风险。这个模型的强大之处在于它非常精确,可以预测99%的市场风险。然而,该模型是根据过去20年的市场行为建立的,不能对剩余1%的意外情况做出预测。可是,随着2007年美国商业银行房贷业务的崩溃,“黑天鹅”真的出现了,整个华尔街措手不及,一次全球大范围的金融危机因此爆发。
2. “检方谬误”:通过统计数据推断出的结论,必定存在误差,不会100%正确。即使误差再小,也不能忽视它的存在。
【案例】假设一名法官被告知:犯罪现场遗留的 DNA 样本和被告的 DNA 相吻合,除了被告以外,这个样本和其他人 DNA 相吻合的概率只有百万分之一。如果仅凭这些证据为被告人定罪,就可能出现冤案。百万分之一的误差看似很小,但警方的 DNA 样本库数量非常庞大,通过样本比对,找到两个 DNA 特征相似的人并非不可能。
金句
1. 对于长期发行、销量稳定的彩票,奖金总额的期望值是恒定的,发行机构只要保证彩票的销售额大于奖金期望值,就肯定能赚钱。
2. 我们不可能通过数据得出完全确凿的真相,只能通过合理控制误差来无限接近真相。
3. 最大的风险从来就不是那些我们能看得见、算得出的,而是那些看上去似乎概率很小,我们认为一辈子都不可能发生的风险。它们的确会发生,而且比我们想象的要频繁得多。
4. 统计学原理虽然看似简单,但却不是人人都能做数据分析师。因为它既能给我们的观点找到严谨的数据支持,但有时也会给一个错误的结论,披上合理的外衣。