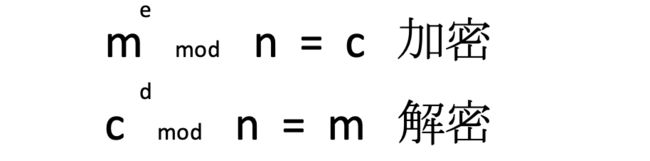欧拉函数 φ (fai, 打出 phi -> φ)
互质: 如果两个正整数,除了1以外,没有其他公因数, 我们就称这两个数是互质关系(coprime)。
计算56的欧拉函数
φ(56) = φ(8)* φ(7) = 4 * 6 = 24
欧拉函数特点:
一、当n是质数的时候,φ(n)=n-1。
二、如果n可以分解成两个互质的整数之积,如n=A*B则:
φ(A*B)=φ(A)* φ(B)
根据以上两点得到:
如果N是两个质数P1 和 P2的乘积则
φ(N)=φ(P1)* φ(P2)=(P1-1)*(P2-1)
欧拉定理
如果两个正整数m和n互质,那么m的φ(n)次方减去1,可以被n整除。
费马小定理
欧拉定理的特殊情况:如果两个正整数m和n互质,而且n为质数!那么φ(n)结果就是n-1。
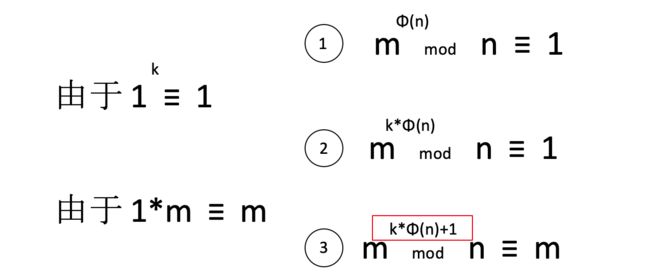
公式转换
例子:
m = 3, n = 5 φ(n) = φ(5) = 4
3 φ(5) mod 5 ---> 3 **4 mod 5 = 81 mod 5 = 1
3 φ(5) mod 5 ---> 3 **(4 * 2) mod 5 = 6561 mod 5 = 1
3 φ(5) mod 5 ---> 3 **(4 + 1) mod 5 = 243 mod 5 = 3
模反元素
如果两个正整数e和x互质,那么一定可以找到整数d,使得 ed-1
被x整除。 那么d就是e对于x的“模反元素”
例子:
e = 3 , x = 5
e*d mod x = 1 --> 3*d mod 5 = 1 , d 可以为 2、7 , 2、7 就是3相对于5的模反元素
e*d = k *x + 1 --> 3*7 = k*5 + 1, k 可以为 4
m = 4, n = 15 , φ(n) = φ(3) * φ(5) = 8, e = 3, d 可以为 11 、19 (d 是求出来的, e*d mod φ(n) = 1 --> 3*d mod 8 = 1 , ---> 3*d - 1 = 8*k ---> d = 3, 11, 19) e和φ(n)互质
4**33 mod 15 = 4 , 5**33 mod 15 = 5 , 6**33 mod 15 = 6
结论 m
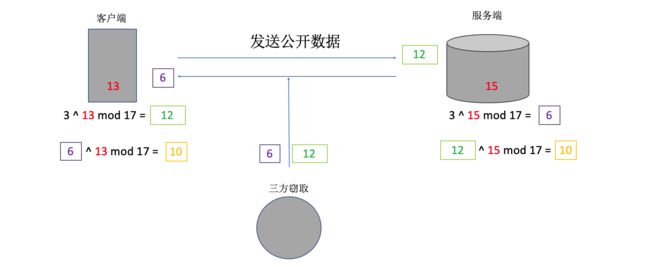
迪菲赫尔曼密钥交换
原理
3 ** 15 mod 17 = 6 , 6 **13 mod 17 = 10 ----> (3 ** 15) ** 13 mod 17 = 10
3 ** 13 mod 17 = 12 , 12 **15 mod 17 = 10 ----> (3 ** 13) ** 15 mod 17 = 10
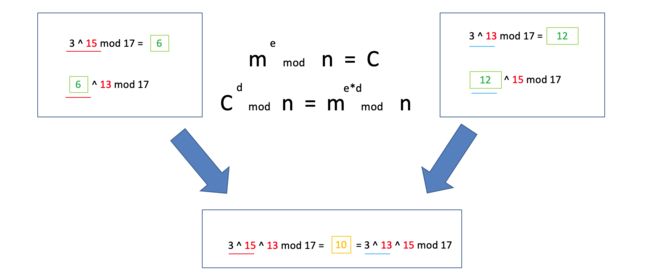
所以 : (3 ** 15)** 13 mod 17 = (3 ** 13) ** 15 mod 17 --->
m **e mod n = c , c ** d mod n = m **(e *d) mod n, m ** (e *d) mod n = m ( d和φ(n)的模反元素 )
m **e mod n = c 加密
c **d mod n = m 解密
RSA算法
例子:
m = 3 , n = 15, φ(n) = 8, e = 3 (与φ(n) 互质),d = 11、19
3 ** 3 mod 15 = 12 , 12 ** 11 mod 15 = 3
12 * 3 mod 15 = 3 , 3 ** 11 mod 15 = 12
m 小于 n, d 是 e 相对于φ(n)的模反元素
公钥: n 和 e
私钥: n 和 d
明文: m
密文: c
n 长度 1024 以上,所以 n 是由 p1 和 p2 两个质数相乘得到的,为了好算。
说明:
1、n会非常大,长度一般为1024个二进制位。(目前人类已经分解的最大整数,232个十进制位,768个二进制位)
2、由于需要求出φ(n),所以根据欧函数特点,最简单的方式n
由两个质数相乘得到: 质数:p1、p2 , Φ(n) = (p1 -1) * (p2 - 1)
3、最终由φ(n)得到e 和 d 。
总共生成6个数字:p1、p2、n、φ(n)、e、d
关于RSA的安全:
除了公钥用到了n和e 其余的4个数字是不公开的。
目前破解RSA得到d的方式如下:
1、要想求出私钥d 。由于e*d = φ(n)*k + 1。要知道e和φ(n);
2、e是知道的,但是要得到 φ(n),必须知道p1 和 p2。
3、由于 n=p1*p2。只有将n因数分解才能算出。
RSA特点总结:(加密核心数据,配合其他加密算法使用)
1. 相对来说比较安全(非对称加密的,私钥不用传递)
2. 效率不高
3. 加密数据小
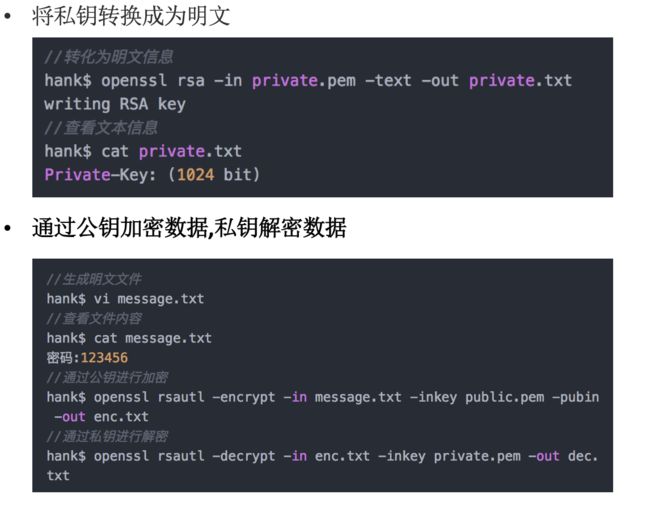
终端演示:
由于Mac系统内置OpenSSL(开源加密库),所以我们可以直接在终端上使用命令来玩RSA.
OpenSSL中RSA算法常用指令主要有三个:
$ openssl genrsa -out private.pem 1024
$ cat private.pem (查看显示出来的是 base64的编码)
$ openssl rsa -in private.pem -pubout -out public.pem
$ openssl rsa -in private.pem -text -out private.txt
$ openssl rsautl -encrypt -in message.txt -inkey public.pem -pubin -out enc.txt 加密
$ openssl rsautl -decrypt -in enc.txt -inkey private.pem -out dec.txt 解密
$ openssl req -new -key private.pem -out rsacert.csr 生成csr文件
$ openssl x509 -req -days 3650 -in rsacert.csr -signkey private.pem -out rsacert.crt 签名
$ openssl pkcs12 -export -out p.p12 -inkey private.pem -in rsacert.crt 生成p12
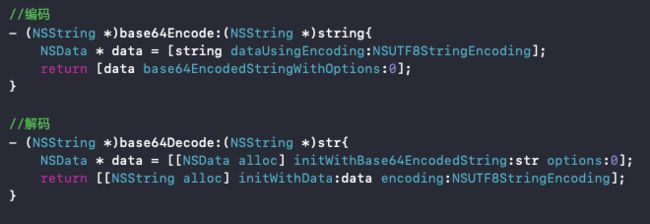
base64
base64 可以将任意的二进制数据进行编码。 编码成为65个字符组成的文本文件。
0~9a ~ z, A ~ Z + / =
$base64 源文件 -o 目标文件 编码
$base64 源文件 -o 目标文件 -D 解码
101001 010101 010100 010101
A 字节 = =
010000 010000 000000 000000 (将二进制数据以每6个二进制为一组进行编码, 6位正好是64个二进制)
例如 : A 的ASCII 码为65, 占1个字节,8个二进制位 01000001 ,---> 010000 010000 000000 000000 (补两组0是为了字节对齐)
RSADemo
$ openssl x509 -outform der -in rsacert.crt -out rsacert.der (在ios中不能直接使用,需将crt 文件生成一个der文件)
将der 和 p12文件拖入项目中,导入 RSACryptor
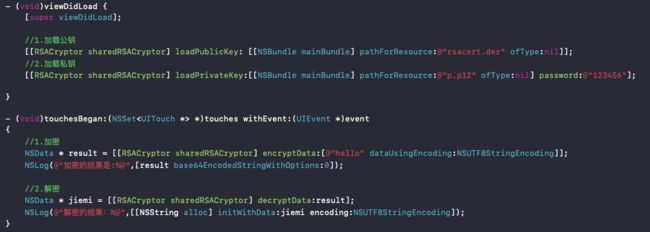
- (void)viewDidLoad {
[super viewDidLoad];
//1.加载公钥
[[RSACryptor sharedRSACryptor] loadPublicKey: [[NSBundle mainBundle] pathForResource:@"rsacert.der" ofType:nil]];
//2.加载私钥
[[RSACryptor sharedRSACryptor] loadPrivateKey:[[NSBundle mainBundle] pathForResource:@"p.p12" ofType:nil] password:@"123456"];
}
- (void)touchesBegan:(NSSet *)touches withEvent:(UIEvent*)event{
//1.加密
NSData * result = [[RSACryptor sharedRSACryptor] encryptData:[@"hello" dataUsingEncoding:NSUTF8StringEncoding]];
NSLog(@"加密的结果是:%@",[result base64EncodedStringWithOptions:0]);
//2.解密
NSData * jiemi = [[RSACryptor sharedRSACryptor] decryptData:result];
NSLog(@"解密的结果:%@",[[NSString alloc] initWithData:jiemi encoding:NSUTF8StringEncoding]);
}
加密结果不一样
// 填充模式 kSecPaddingNone 每次解密结果是固定的
// kSecPaddingPKCS1 是随机变化的。
#define kTypeOfWrapPadding kSecPaddingNone