朴素贝叶斯 naive bayes

背景案例

几年前，J.K. 罗琳（凭借《哈利波特》出名）试着做了件有趣的事。她以 Robert Galbraith 的化名写了本名叫《The Cuckoo’s Calling》的书。尽管该书得到一些不错的评论，但是大家都不太重视它，直到 Twitter 上一个匿名的知情人士说那是 J.K. Rowling 写的。《伦敦周日泰晤士报》找来两名专家对《杜鹃在呼唤》和 Rowling 的《偶发空缺》以及其他几名作者的书进行了比较。分析结果强有力地指出罗琳就是作者，《泰晤士报》直接询问出版商情况是否属实，而出版商也证实了这一说法，该书在此后一夜成名。

这就是一个文本分类预测的例子，接下来我们看看朴素贝叶斯是怎么做的。

贝叶斯定理

贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。
这个定理解决了现实生活里经常遇到的问题：已知某条件概率，如何得到两个事件交换后的概率，也就是在已知P(A|B)的情况下如何求得P(B|A)。

条件概率：

贝叶斯定理：

朴素贝叶斯

朴素贝叶斯之所以朴素，是因为其思想很朴素，英文 naive .....（不禁想到某位长者）。在文本分类上，其忽略了词序，记录词频。朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。

优点：

易执行
特征空间大
有效

缺点：

无语义分析

朴素贝叶斯分类的正式定义如下：

设

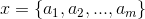
为一个待分类项，而每个a为x的一个特征属性。
有类别集合

。
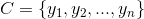
计算

。
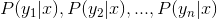
如果

，则

。

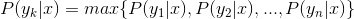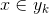
那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做：

找到一个已知分类的待分类项集合，这个集合叫做训练样本集。
统计得到在各类别下各个特征属性的条件概率估计。即

如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：

因为分母对于所有类别为常数，因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有：

流程

第一阶段——准备工作阶段，这个阶段的任务是为朴素贝叶斯分类做必要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，然后由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。

第二阶段——分类器训练阶段，这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序自动计算完成。

第三阶段——应用阶段。这个阶段的任务是使用分类器对待分类项进行分类，其输入是分类器和待分类项，输出是待分类项与类别的映射关系。这一阶段也是机械性阶段，由程序完成。

Example

病人分类的例子

让我从一个例子开始讲起，你会看到贝叶斯分类器很好懂，一点都不难。
某个医院早上收了六个门诊病人，如下表。

    症状　　职业　　　疾病
　　打喷嚏　护士　　　感冒 
　　打喷嚏　农夫　　　过敏 
　　头痛　　建筑工人　脑震荡 
　　头痛　　建筑工人　感冒 
　　打喷嚏　教师　　　感冒 
　　头痛　　教师　　　脑震荡

现在又来了第七个病人，是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大？

根据贝叶斯定理：
P(A|B) = P(B|A) P(A) / P(B)

可得

P(感冒|打喷嚏x建筑工人) 
　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
　　　　/ P(打喷嚏x建筑工人)

假定"打喷嚏"和"建筑工人"这两个特征是独立的，因此，上面的等式就变成了

P(感冒|打喷嚏x建筑工人) 
　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒) 
　　　　/ P(打喷嚏) x P(建筑工人)

这是可以计算的

P(感冒|打喷嚏x建筑工人) 
　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
　　　　= 0.66

因此，这个打喷嚏的建筑工人，有66%的概率是得了感冒。同理，可以计算这个病人患上过敏或脑震荡的概率。比较这几个概率，就可以知道他最可能得什么病。
这就是贝叶斯分类器的基本方法：在统计资料的基础上，依据某些特征，计算各个类别的概率，从而实现分类。

实战

我们有一组邮件，分别由同一家公司的两个人撰写其中半数的邮件。我们的目标是仅根据邮件正文区分每个人写的邮件。

先给你一个字符串列表。每个字符串代表一封经过预处理的邮件的正文；提供代码，用来将数据集分解为训练集和测试集。

朴素贝叶斯特殊的一点在于，这种算法非常适合文本分类。在处理文本时，常见的做法是将每个单词看作一个特征，这样就会有大量的特征。此算法的相对简单性和朴素贝叶斯独立特征的这一假设，使其能够出色完成文本的分类。此项目使用 python 的 sklearn包，然后使用朴素贝叶斯根据作者对邮件进行分类。

#!/usr/bin/python

    
import sys
from time import time
sys.path.append("../tools/")
from email_preprocess import preprocess
from sklearn.metrics import accuracy_score

### features_train and features_test are the features for the training
### and testing datasets, respectively
### labels_train and labels_test are the corresponding item labels
features_train, features_test, labels_train, labels_test = preprocess()

#########################################################
### main code ###
from sklearn.naive_bayes import GaussianNB

# 创建分类器
clf = GaussianNB()
t0 = time()
clf.fit(features_train, labels_train)
print "training time:", round(time()-t0, 3), "s"

t1 = time()
# 进行预测
pred = clf.predict(features_test)
print "predicting time:", round(time()-t1, 3), "s"

# 输出预测准确率
print accuracy_score(pred,labels_test)

#########################################################

结果

no. of Chris training emails: 7936
no. of Sara training emails: 7884
training time: 2.396 s
predicting time: 0.464 s

accuracy: 0.973265073948

参考文章

算法杂货铺——分类算法之朴素贝叶斯分类(Naive Bayesian classification))
朴素贝叶斯分类器的应用
Intro to machine learning