吴恩达DeepLearning.ai的Sequence model作业Dinosaurus Island

 

目录

1 问题设置

 

• 1.1 数据集和预处理
• 1.2 概览整个模型

 

2. 创建模型模块

 

• 2.1 在优化循环中梯度裁剪
• 2.2 采样

 

3. 构建语言模型

 

• 3.1 梯度下降
• 3.2 训练模型

 

4. 结论

 

 

 

本文是DeepLearning.ai的第五门课作业: Character level language model - Dinosaurus Island

 

1 问题设置

 

欢迎来到恐龙岛！ 6500万年前，恐龙就已经存在，并且在这种任务下它们又回来了。你负责一项特殊任务。领先的生物学研究人员正在创造新的恐龙品种，并将它们带入地球，而你的工作就是为这些恐龙起名字。如果恐龙不喜欢它的名字，它可能会发疯，所以请明智地选择！

幸运的是，你已经学习了一些深度学习，你将用它来节省时间。你的助手已收集了他们可以找到的所有恐龙名称的列表，并将其编译到此数据集中。要创建新的恐龙名称，你将构建一个字符级语言模型来生成新名称。你的算法将学习不同的名称模式，并随机生成新名称。希望该算法可以使你和你的团队免受恐龙的愤怒！

完成此作业，你将学到：

• 如何存储文本数据以使用RNN进行处理
• 如何通过在每个时间步采样预测并将其传递给下一个RNN单元来合成数据
• 如何构建字符级文本生成循环神经网络
• 为什么剪裁渐变很重要

我们将首先加载rnn_utils中为你提供的一些功能。具体来说，你可以访问rnn_forward和rnn_backward之类的功能，这些功能与你在上一个作业中实现的功能等效。

import numpy as np from utils import * import random import pprint

 

1.1 数据集和预处理

 

以下代码做了三件事:

1. 读取恐龙名称的数据集
2. 创建唯一字符列表（例如a-z）
3. 计算数据集和词汇量。

data = open('dinos.txt', 'r').read() # 加载数据集 
data= data.lower() # 将所有数据变小写 
chars = list(set(data)) # 创建唯一字符列表，data中用了什么字符 
data_size, vocab_size = len(data), len(chars) # 数据集的大小和词汇量 
print('There are %d total characters and %d unique characters in your data.' % (data_size, vocab_size))

char_to_ix：在下面的单元格中，我们创建一个python字典（即哈希表），以将每个字符映射到0-26之间的索引。

ix_to_char：我们还创建了第二个python字典，该字典将每个索引映射回相应的字符。 这将帮你找出softmax层的概率分布输出中哪个索引对应于哪个字符。

chars = sorted(chars) print(chars)

['\n', 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z']

char_to_ix = { ch:i for i,ch in enumerate(chars) } ix_to_char = { i:ch for i,ch in enumerate(chars) } pp = pprint.PrettyPrinter(indent=4) # 格式化输出 pp.pprint(ix_to_char)

{ 0: '\n', 1: 'a', 2: 'b', 3: 'c', 4: 'd', 5: 'e', 6: 'f', 7: 'g', 8: 'h', 9: 'i', 10: 'j', 11: 'k', 12: 'l', 13: 'm', 14: 'n', 15: 'o', 16: 'p', 17: 'q', 18: 'r', 19: 's', 20: 't', 21: 'u', 22: 'v', 23: 'w', 24: 'x', 25: 'y', 26: 'z'}

 

1.2 概览整个模型

 

你的模型将具有以下结构：

• 初始化参数
• 运行优化循环
• 前向传播以计算损失函数
• 向后传播根据损失函数计算梯度
• 梯度裁剪以避免梯度爆炸
• 使用梯度下降规则更新你的参数

• 返回学习到的参数

• 每一个时间步长, RNN都会根据之前的字符来预测下一个字符是什么。
• 数据集 \mathbf{X} = (x^{\langle 1 \rangle}, x^{\langle 2 \rangle}, ..., x^{\langle T_x \rangle}) 是训练集中的字符列表。
• \mathbf{Y} = (y^{\langle 1 \rangle}, y^{\langle 2 \rangle}, ..., y^{\langle T_x \rangle}) 是相同的字符列表，但是向前移动了一个字符。
• 每个时间步长 t, y^{\langle t \rangle} = x^{\langle t+1 \rangle}. 在时间 t 处的预测值和时间 t + 1 处的输入值相同.

 

2. 创建模型模块

 

在这一部分中，你将构建整个模型的两个重要模块：

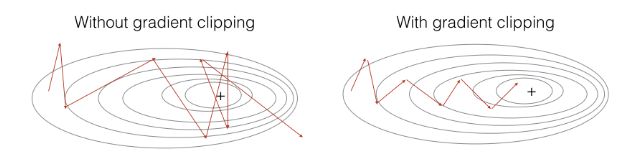
• 梯度裁剪：避免梯度爆炸
• 采样：一种用于生成字符的技术

然后，你将应用这两个功能来构建模型。

 

2.1 在优化循环中梯度裁剪

 

在本节中，你将实现在优化循环中调用的clip函数。

梯度爆炸

• 当梯度值非常大时，称为“梯度爆炸”。
• 梯度爆炸使训练过程更加困难，因为更新可能太大，以至于在反向传播过程中“overshoot”了最佳值。

回想一下，你的总循环结构通常包括：

• 向前传播
• 计算成本函数
• 向后传播
• 参数更新

在更新参数之前，你需要执行梯度裁剪，以确保梯度不“爆炸”。

 

梯度裁剪

 

在下面的练习中，你将实现一个函数clip，该函数接受梯度字典，并在需要时返回梯度的裁剪版本。

• 剪切渐变有多种方法。
• 我们将使用简单的按元素裁剪程序，其中将梯度向量的每个元素裁剪为位于某个范围[-N，N]之间。
• 例如，如果N = 10
• 元素的取值范围是[-10，10]
• 如果任何在梯度向量中大于10的元素，则将其设置为10。
• 如果任何在梯度向量中小于-10的元素，则将其设置为-10。
• 如果任何在-10到10之间的元素，则它们保持原始值。

在遇到“梯度爆炸”问题情况下，带和不带梯度裁剪的梯度下降的可视化图。

返回字典“ gradients”的剪裁梯度。

def clip(gradients, maxValue):
'''
Clips the gradients' values between minimum and maximum.

Arguments:
gradients -- a dictionary containing the gradients "dWaa", "dWax", "dWya", "db", "dby"
maxValue -- everything above this number is set to this number, and everything less than -maxValue is set to -maxValue

Returns:
gradients -- a dictionary with the clipped gradients.
'''

dWaa, dWax, dWya, db, dby = gradients['dWaa'], gradients['dWax'], gradients['dWya'], gradients['db'], gradients['dby']

### START CODE HERE ###
# clip to mitigate exploding gradients, loop over [dWax, dWaa, dWya, db, dby]. (≈2 lines)
for gradient in [dWax, dWaa, dWya, db, dby]:
np.clip(gradient, -maxValue, maxValue, out=gradient)
### END CODE HERE ###

# gradients = {"dWaa": dWaa, "dWax": dWax, "dWya": dWya, "db": db, "dby": dby}

return gradients

 

2.2 采样

 

现在假设你的模型已经过训练，你想生成新文本（字符），下图说明了生成过程：

在这张照片中，我们假设模型已经过训练。 我们在第一个时间步长中传入x^{\langle 1\rangle} = \vec{0}，然后让网络一次采样一个字符。

练习: 执行下面的 sample函数来采样字符，你需要4步:

• Step 1: 输入0的 "dummy" 向量x^{\langle 1 \rangle} = \vec{0}.
• 这是我们生成任何字符之前的默认输入。 我们还设置了 a^{\langle 0 \rangle} = \vec{0}

 

• Step 2: 执行一次向前传播即可获得 a^{\langle 1 \rangle} 和 \hat{y}^{\langle 1 \rangle}. 这里是公式:

隐藏状态:

激活:

预测:

• 关于 的一些细节:
• 注意 是一个概率向量 (softmax) (它的每个元素值在0到1之间，且总和为1).
• 表示由“ i”索引的字符是下一个字符的概率。
• 我们提供了 softmax() 函数供你使用.

额外的提示

• x^{\langle 1 \rangle} 在代码中是 x.当创建one-hot向量时，请创建一个由零的组成numpy数组，其中行数等于唯一字符数，列数等于1。 它是2D而不是1D数组。
• a^{\langle 0 \rangle} 在代码中是a_prev. 它是一个由零组成的numpy数组，其中行数为 n_ {a} ，列数为1。它也是2D数组。 通过获取 W_ {aa} 中的列数来得到 n_ {a} （这些数字必须匹配，以便矩阵乘法W_{aa}a^{\langle t \rangle}起作用 。
• a ^ {\ langle 0 \ rangle} 在代码中为a_prev。
• numpy.dot
• numpy.tanh

用2维而不是1维

• 你可能想知道为什么我们强调x^{\langle 1 \rangle}和a^{\langle 0 \rangle}是2D数组而不是1D向量。
• 对于numpy中的矩阵乘法，如果将2D矩阵与1D向量相乘，则最终得到1D数组。
• 当我们将两个数组相加时，期望它们具有相同形状，这将成为一个问题。
• 当两个具有不同维数的数组加在一起时，Python将会执行“广播broadcasts”。
• 这是一些示例代码，显示了使用1D和2D数组之间的区别。

import numpy as np 
matrix1 = np.array([[1,1],[2,2],[3,3]]) # (3,2) 
matrix2 = np.array([[0],[0],[0]]) # (3,1) 
vector1D = np.array([1,1]) # (2,) 
vector2D = np.array([[1],[1]]) # (2,1) 
np.dot(matrix1,vector1D) # 2D 和 1D 数组相乘: 结果是1D数组 [2 4 6] 
np.dot(matrix1,vector2D) # 2D 和 2D 数组相乘: 结果是2D数组 [[2], [4], [6]] 
np.dot(matrix1,vector2D) + matrix2 # (3 x 1) 向量和(3 x 1)向量相加是(3 x 1) 向量，这个是我们想要的。 [[2] [4] [6]] 
np.dot(matrix1,vector1D) + matrix2 # (3,) 向量和(3 x 1)向量相加，这会在第二维上广播1D的数组，这不是我们想要的！

 

• Step 3: 抽样:
• 注意我们已经有了y^{\langle t+1 \rangle}, 我们想选择恐龙名称中的下一个字母。如果我们选择最有可能的情况，那么在给定起始字母的情况下，模型将始终产生相同的结果。
• 为了使结果更有趣，我们将使用np.random.choice选择可能但并非总是相同的下一个字母。

 

• 采样是从一组值中选择一个值，其中每个值都有一定概率被选择。
• 采样使我们能够生成随机的序列值。
• 根据\hat{y}^{\langle t+1 \rangle }中的概率分布选择下一个字符的索引。
• 这就意味着如果\hat{y}^{\langle t+1 \rangle }_i = 0.16, 你将以16％的概率选择索引“ i”。
• 你可以查看np.random.choice.

这里有个例子np.random.choice(): np.random.seed(0) probs = np.array([0.1, 0.0, 0.7, 0.2]) idx = np.random.choice([0, 1, 2, 3] p = probs)

• 这就意味着你会根据分布来选择索引:

P(index = 0) = 0.1, P(index = 1) = 0.0, P(index = 2) = 0.7, P(index = 3) = 0.2.

• 注意p的值是1D向量。
• 注意 \hat{y}^{\langle t+1 \rangle}在代码中用 y 表示, 它是2维数组。

• Step 4: 更新 x^{\langle t \rangle }
• sample()函数的最后一步就是更新变量x, 它当前存储的是 x^{\langle t \rangle }, 换成x^{\langle t + 1 \rangle }.
• 你将选择作为预测字符相对应的one-hot矢量来代表x^{\langle t + 1 \rangle }。
• 你将接着在步骤1中向前传播x^{\langle t + 1 \rangle }，并继续重复该过程直到获得“ \n”字符，它表明你已经到达恐龙名称的末尾。

# GRADED FUNCTION: sample

def sample(parameters, char_to_ix, seed):
    """
    Sample a sequence of characters according to a sequence of probability distributions output of the RNN

    Arguments:
    parameters -- python dictionary containing the parameters Waa, Wax, Wya, by, and b. 
    char_to_ix -- python dictionary mapping each character to an index.
    seed -- used for grading purposes. Do not worry about it.

    Returns:
    indices -- a list of length n containing the indices of the sampled characters.
    """
    
    # Retrieve parameters and relevant shapes from "parameters" dictionary
    Waa, Wax, Wya, by, b = parameters['Waa'], parameters['Wax'], parameters['Wya'], parameters['by'], parameters['b']
    vocab_size = by.shape[0]
    n_a = Waa.shape[1]
    
    ### START CODE HERE ###
    # Step 1: Create the a zero vector x that can be used as the one-hot vector 
    # representing the first character (initializing the sequence generation). (≈1 line)
    x = np.zeros((vocab_size, 1)) # 可以看看上面为什么这里是二维
    # Step 1': Initialize a_prev as zeros (≈1 line)
    a_prev = np.zeros((n_a, 1))
    
    # Create an empty list of indices, this is the list which will contain the list of indices of the characters to generate (≈1 line)
    indices = []
    
    # idx is the index of the one-hot vector x that is set to 1
    # All other positions in x are zero.
    # We will initialize idx to -1
    idx = -1 
    
    # Loop over time-steps t. At each time-step:
    # sample a character from a probability distribution 
    # and append its index (`idx`) to the list "indices". 
    # We'll stop if we reach 50 characters 
    # (which should be very unlikely with a well trained model).
    # Setting the maximum number of characters helps with debugging and prevents infinite loops. 
    counter = 0
    newline_character = char_to_ix['\n']
    
    while (idx != newline_character and counter != 50):
        
        # Step 2: Forward propagate x using the equations (1), (2) and (3)
        a = np.tanh(np.dot(Wax, x) + np.dot(Waa, a_prev) + b)
        z = np.dot(Wya, a) + by
        y = softmax(z)
        
        # for grading purposes
        np.random.seed(counter+seed) 
        
        # Step 3: Sample the index of a character within the vocabulary from the probability distribution y
        # (see additional hints above)
        idx = np.random.choice(list(range(vocab_size)), p=y.ravel())

        # Append the index to "indices"
        indices.append(idx)
        
        # Step 4: Overwrite the input x with one that corresponds to the sampled index `idx`.
        # (see additional hints above)
        x = np.zeros((vocab_size, 1))
        x[idx] = 1
        
        # Update "a_prev" to be "a"
        a_prev = a
        
        # for grading purposes
        seed += 1
        counter +=1
        
    ### END CODE HERE ###

    if (counter == 50):
        indices.append(char_to_ix['\n'])
    
    return indices

 

3. 构建语言模型

3.1 梯度下降

现在是时候建立用于文字生成的字符级语言模型了。

• 在本节中，你将实现一个函数，该函数执行一步随机梯度下降（带有修剪的梯度）。
• 你将一次查看一个训练示例，因此优化算法将是随机梯度下降。

提醒一下，这是RNN常见优化循环的步骤:

• 通过RNN向前传播以计算损耗
• 随时间向后传播以计算相对于参数的损耗梯度
• 梯度裁剪
• 使用梯度下降更新参数

Exercise: 实施优化过程（随机梯度下降的一步）

已提供以下函数:

def rnn_forward(X, Y, a_prev, parameters):
    """ Performs the forward propagation through the RNN and computes the cross-entropy loss.
    It returns the loss' value as well as a "cache" storing values to be used in backpropagation."""
    ....
    return loss, cache

def rnn_backward(X, Y, parameters, cache):
    """ Performs the backward propagation through time to compute the gradients of the loss with respect
    to the parameters. It returns also all the hidden states."""
    ...
    return gradients, a

def update_parameters(parameters, gradients, learning_rate):
    """ Updates parameters using the Gradient Descent Update Rule."""
    ...
    return parameters
Recall that you previously implemented the clip function:

def clip(gradients, maxValue)
    """Clips the gradients' values between minimum and maximum."""
    ...
    return gradients

• 请注意，即使parameters不是optimize函数的返回值之一，parameters字典中的权重和偏差也会通过优化进行更新。参数字典通过引用传递到函数中，因此即使在函数外部访问该字典，对字典的更改也会对参数字典做出更改。
• Python字典和列表是“按引用传递”，这意味着，如果将字典传递给函数并在函数内修改字典，则这将更改同一字典。

def optimize(X, Y, a_prev, parameters, learning_rate = 0.01):
    """
    Execute one step of the optimization to train the model.
    
    Arguments:
    X -- list of integers, where each integer is a number that maps to a character in the vocabulary.
    Y -- list of integers, exactly the same as X but shifted one index to the left.
    a_prev -- previous hidden state.
    parameters -- python dictionary containing:
                        Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x)
                        Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a)
                        Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a)
                        b --  Bias, numpy array of shape (n_a, 1)
                        by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1)
    learning_rate -- learning rate for the model.
    
    Returns:
    loss -- value of the loss function (cross-entropy)
    gradients -- python dictionary containing:
                        dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x)
                        dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a)
                        dWya -- Gradients of hidden-to-output weights, of shape (n_y, n_a)
                        db -- Gradients of bias vector, of shape (n_a, 1)
                        dby -- Gradients of output bias vector, of shape (n_y, 1)
    a[len(X)-1] -- the last hidden state, of shape (n_a, 1)
    """
    
    ### START CODE HERE ###
    
    # Forward propagate through time (≈1 line)
    loss, cache = rnn_forward(X, Y, a_prev, parameters)
    
    # Backpropagate through time (≈1 line)
    gradients, a = rnn_backward(X, Y, parameters, cache)
    
    # Clip your gradients between -5 (min) and 5 (max) (≈1 line)
    gradients = clip(gradients, 5)
    
    # Update parameters (≈1 line)
    parameters = update_parameters(parameters, gradients, learning_rate)
    
    ### END CODE HERE ###
    
    return loss, gradients, a[len(X)-1]

 

3.2 训练模型

• 给定恐龙名称数据集，我们将数据集的每一行（一个名称）用作一个训练样本。
• 每100步随机梯度下降，你将抽样10个随机选择的名称，以查看算法的运行情况。
• 请记住要对数据集进行混洗，以便随机梯度下降以随机顺序访问样本。

锻炼：按照说明进行操作并实现model（）。当examples[index]包含一个恐龙名称（字符串）以创建示例（X，Y）时，可以使用以下方法：

将索引idx设置为样本列表

• 使用for循环，在“示例”列表中浏览经过排序的恐龙名称列表。
• 如果有100个示例，并且for循环将索引从100开始递增，请考虑如何使索引循环回到0，以便我们可以在j为100、101，等等
• 提示：101除以100为零，余数为1。
• ％是python中的模运算符。

从示例列表中提取一个示例 *single_example：使用你先前设置的idx索引从示例列表中获取一个单词。

def model(data, ix_to_char, char_to_ix, num_iterations = 35000, n_a = 50, dino_names = 7, vocab_size = 27):
    """
    Trains the model and generates dinosaur names. 
    
    Arguments:
    data -- text corpus
    ix_to_char -- dictionary that maps the index to a character
    char_to_ix -- dictionary that maps a character to an index
    num_iterations -- number of iterations to train the model for
    n_a -- number of units of the RNN cell
    dino_names -- number of dinosaur names you want to sample at each iteration. 
    vocab_size -- number of unique characters found in the text (size of the vocabulary)
    
    Returns:
    parameters -- learned parameters
    """
    
    # Retrieve n_x and n_y from vocab_size
    n_x, n_y = vocab_size, vocab_size
    
    # Initialize parameters
    parameters = initialize_parameters(n_a, n_x, n_y)
    
    # Initialize loss (this is required because we want to smooth our loss)
    loss = get_initial_loss(vocab_size, dino_names)
    
    # Build list of all dinosaur names (training examples).
    with open("dinos.txt") as f:
        examples = f.readlines()
    examples = [x.lower().strip() for x in examples]
    
    # Shuffle list of all dinosaur names
    np.random.seed(0)
    np.random.shuffle(examples)
    
    # Initialize the hidden state of your LSTM
    a_prev = np.zeros((n_a, 1))
    
    # Optimization loop
    for j in range(num_iterations):
        
        ### START CODE HERE ###
        
        # Set the index `idx` (see instructions above)
        index = j % len(examples)
        
        # Set the input X (see instructions above)
        single_example = examples[index]
        single_example_chars = [ch for ch in single_example]
        single_example_ix = [char_to_ix[ch] for ch in single_example_chars] 
        X = [None] + single_example_ix 
        
        # Set the labels Y (see instructions above)
        ix_newline = char_to_ix["\n"]
        Y = X[1:] + [ix_newline]
        
        # Perform one optimization step: Forward-prop -> Backward-prop -> Clip -> Update parameters
        # Choose a learning rate of 0.01
        curr_loss, gradients, a_prev = optimize(X, Y, a_prev, parameters)
        
        ### END CODE HERE ###
        
        # Use a latency trick to keep the loss smooth. It happens here to accelerate the training.
        loss = smooth(loss, curr_loss)

        # Every 2000 Iteration, generate "n" characters thanks to sample() to check if the model is learning properly
        if j % 2000 == 0:
            
            print('Iteration: %d, Loss: %f' % (j, loss) + '\n')
            
            # The number of dinosaur names to print
            seed = 0
            for name in range(dino_names):
                
                # Sample indices and print them
                sampled_indices = sample(parameters, char_to_ix, seed)
                print_sample(sampled_indices, ix_to_char)
                
                seed += 1  # To get the same result (for grading purposes), increment the seed by one. 
      
            print('\n')
        
    return parameters

运行以下代码，你应该观察到模型在第一次迭代时输出看似随机的字符。 经过数千次迭代后，你的模型应该学会生成看起来合理的名称。

 

parameters = model(data, ix_to_char, char_to_ix)

 

输出可能像是以下这样的:

Iteration: 34000, Loss: 22.447230

Onyxipaledisons

Kiabaeropa

Lussiamang

Pacaeptabalsaurus

Xosalong

Eiacoteg

Troia

 

4. 结论

 

你可以看到，在训练即将结束时，你的算法已开始生成合理的恐龙名称。刚开始时，它会生成随机字符，但是到最后，你会看到恐龙名字的结尾很酷。当运行完代码后，它会生成一个酷炫的名字: Mangosaurus!