棋盘问题的递归解决

具体的题目是：
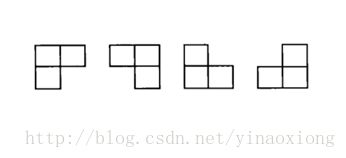
有一个 的方格棋盘，恰有一个方格是黑色的，其它为白色。你的任务是用包含3个方格的L型牌覆盖所有白色方格。黑方格不能被覆盖，且任意一个白色方格不能同时被两个或者多个L型牌覆盖。如图为L型牌的4种旋转方式。

4种方式

问题分析：
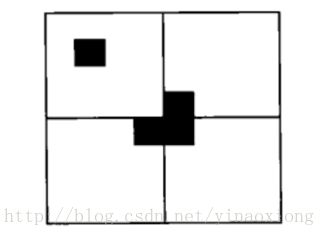
我们很容易想到用递归的方法去解决这个问题，在经典的递归问题汉诺塔问题中我们，把N个盘子的问题分解成N-1个问题去递归解决。那么我们也可以往这方面想，这个棋盘规格是2^k*2K，那么我们可以将k减去1，将大棋盘分成小棋盘来解决。于是大棋盘被分成了四个小棋盘，可是新的问题来了，虽然把棋盘分解了可是只有一个棋盘里是有黑块的，这样没法进行递归。既然没有那么我们就想办法给它添上，而且每分一次就添一次，保证递归的进行。问题的关键是怎么添，添在哪里？根据这个L形的形状，可以在分割的中心的添上一个L形。如图所示：

这里写图片描述

然后递归就可以顺利的进行了。总结一下过程：

1. 递归的结束条件当：k=0时，也就是不在是一个棋盘的时候，可能会有人问问什么不是k=1时，因为k=1时依然需要继续把另外三个地方添上黑块。
2. 递归关系，将大棋盘分解为小棋盘递归解决。

好了不说了上代码：

#include 
#include 
#include

int nCount = 0;
int Matrix[100][100];

void chessBoard(int tr, int tc, int dr, int dc, int size);

int main()
{
    int size, r, c, row, col;
    memset(Matrix, 0, sizeof(Matrix));
    scanf_s("%d", &size);
    scanf_s("%d%d", &row, &col);
    chessBoard(0, 0, row, col, size);

    for (r = 0; r < size; r++)
    {
        for (c = 0; c < size; c++)
        {
            printf("%2d ", Matrix[r][c]);
        }
        printf("\n");
    }

    return 0;
}

void chessBoard(int tr, int tc, int dr, int dc, int size)
{
    int s, t;
    if (1 == size) return;
    s = size / 2;
    t = ++nCount;
    if (dr < tr + s && dc < tc + s)
    {
        chessBoard(tr, tc, dr, dc, s);
    }
    else
    {
        Matrix[tr + s - 1][tc + s - 1] = t;
        chessBoard(tr, tc, tr + s - 1, tc + s - 1, s);
    }

    if (dr < tr + s && dc >= tc + s)
    {
        chessBoard(tr, tc + s, dr, dc, s);
    }
    else
    {
        Matrix[tr + s - 1][tc + s] = t;
        chessBoard(tr, tc + s, tr + s - 1, tc + s, s);
    }
    if (dr >= tr + s && dc < tc + s)
    {
        chessBoard(tr + s, tc, dr, dc, s);
    }
    else
    {
        Matrix[tr + s][tc + s - 1] = t;
        chessBoard(tr + s, tc, tr + s, tc + s - 1, s);
    }
    if (dr >= tr + s && dc >= tc + s)
    {
        chessBoard(tr + s, tc + s, dr, dc, s);
    }
    else
    {
        Matrix[tr + s][tc + s] = t;
        chessBoard(tr + s, tc + s, tr + s, tc + s, s);
    }

}

这是我的一点点理解，有什么不对的请大家批评指正，欢迎评论。