AdderNet: Do We Really Need Multiplications in Deep Learning?
引言
如今的卷积神经网络(CNN)的卷积操作中包含了大量的乘法，虽然已经有很多轻量级的网络(如MobileNet)提出来，但是乘法的开销依旧是难以忽视的，要在轻量级设备本地进行深度学习应用，需要使得计算速度进一步加快，于是本论文提出了使用加法操作代替乘法操作，本论文的作者是Hanting Chen,Yunhe Wang,Chunjing Xu,Boxin Shi,Chao Xu,Qi Tian,Chang Xu。是CVPR2020上华为诺亚实验室和北京大学合作的一篇文章。
论文指出传统卷积操作其实就是使用的一种互相关操作来衡量输入特征和卷积核之间的相似度，而这个互相关的操作就引入了很多乘法操作，因此文章提出另一种方式来衡量输入特征和卷积核之间的相似度，这个方法就是L1距离。
没有乘法的网络
假设$F \in R^{d \times d \times c_in \times c_{out}}$，F是网络中间某层的过滤器，过滤器大小为d，输入有$c_{in}$个通道，输出有$c_{out}$个通道。输入的特征定义为$X \in R^{H \times W \times c_{in}}$，其中H和W对应着特征的高和宽。则输出的Y有以下式子$$Y(m,n,t) = \sum_{i=0}^n \sum_{j=0}^d \sum_{k=0}^{c_{in}}S(X(m+i,n+j,k),F(i,j,k,t))$$其中S是相似度函数。如果$S(x,y) = x \times y$,那么这个公式就变成了传统卷积神经网络中的卷积操作。
加法网络
前面提到过要用L1距离代替互相关操作，那么上述公式就变成$$Y(m,n,t) = - \sum_{i=0}^n \sum_{j=0}^d \sum_{k=0}^{c_{in}}|X(m+i,n+j,k)-F(i,j,k,t)|$$这里作者提到了这样的操作得出的结果都是负值，但是传统卷积网络得到的输出值则是有正有负，但是在输出层后紧接着一个BN层我们可以让输出分布在一个合理的范围。
优化
在传统卷积网络中Y关于F的反向传播公式如下$$\frac{\partial Y(m,n,t)}{\partial F(i,j,k,t) } = X(m+i,n+j,k)$$在加法网络中，使用了L1距离的反向传播公式如下$$\frac{\partial Y(m,n,t)}{\partial F(i,j,k,t)} = sgn(X(m+i,n+j,k) - F(i,j,k,t))$$文章中说L1距离反向传播的这种signSGD并不能沿着最好的方向下降，有时候还会选择比较糟糕的方向，因此论文中把反向传播公式变成L2距离的反向传播，叫做全精度梯度$$\frac{\partial Y(m,n,t)}{\partial F(i,j,k,t) } = X(m+i,n+j,k) - F(i,j,k,t)$$同时再考虑Y对X的导数，根据链式法则，$\frac{\partial Y}{\partial F_i }$只跟$F_i$自己有关，而$\frac{\partial Y}{\partial X_i }$的梯度值还会影响前一层的值，作者指出这种全精度梯度传播会产生梯度爆炸，于是使用一个HT函数把梯度截断在[-1,1]里，既$$\frac{\partial Y(m,n,t)}{\partial X(m+i,n+j,k) } = HT(F(i,j,k,t) - F(i,j,k,t))$$其中HT代表着HardTanh函数$$HT(x) = x\quad if -1
自适应学习率
在加法网络中，每一层输出后面也跟着一层BN层，虽然BN层带来了一些乘法操作，但是这些操作的量级比起经典卷积网络的乘法数量就可以忽略不计。给定一个mini-batch B={x1,...,xm}，BN层做了如下操作$$y = \gamma \frac{x-\mu_B}{\sigma_B}+\beta$$$$\mu=\frac{1}{m}\sum_ix_i$$$$\sigma_B^2=\frac{1}{m}\sum_i(x_i-\mu_B)^2$$该层主要就是处理这个mini-batch的数据集使它均值等于0，方差等于1。那么加上了BN层后l关于x的偏导为$$\frac{\partial l}{\partial x_i}=\sum_{j=1}^m\frac{\gamma}{m^2\sigma_B}\{\frac{\partial l}{\partial y_i}-\frac{\partial l}{\partial y_j}[1+\frac{(x_i-x_j)(x_j-\mu_B)}{\sigma_B}]\}$$根据链式法则，每一层的权重的梯度都受到上一层$x_i$梯度的影响，根据上述公式$x_i$的梯度很大程度取决于$\sigma_B$，即BN处理前$x_i$的标准差。论文中给出了粗略的输出Y的方差计算，传统神经网络输出方差为$$Var[Y_{CNN}]=\sum_{i=0}^d \sum_{j=0}^d \sum_{k=0}^{c_{in}}Var[X \times F]=d^2c_{in}Var[X]Var[F]$$而在加法网络中方差变为$$Var[Y_{CNN}]=\sum_{i=0}^d \sum_{j=0}^d \sum_{k=0}^{c_{in}}Var[|X-F|]=(1-\frac{2}{\pi})d^2c_{in}(Var[X]+Var[F])$$根据以往经验，$Var[F]$在普通CNN网络中非常的小，只有$10^{-3}$或者$10^{-4}$。因此传统CNN中$Var[Y]$方差要比加法网络中$Var[Y]$大很多。之前提到权重梯度取决于标准差，因此用了BN层的加法网络中权重梯度会很小，下表是个对比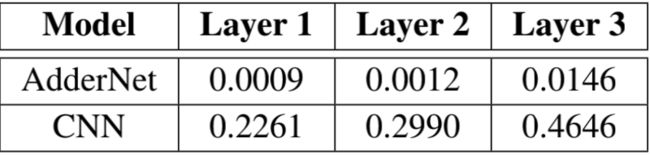
图片除显示出梯度较小之外，还展示出有些层可能值不在一个量级，因此使用全局统一的学习率变得不再合适，所以论文中使用了一种自适应学习率的方法，使得学习率在每一层都不一样。它的公式计算表示为$$\Delta F_l = \gamma \times \alpha_l \times \Delta L(F_l)$$其中$\gamma$是全局学习率，而$\alpha_l$则是每层的学习率。$$\alpha_l = \frac{\eta \sqrt k}{\parallel \Delta L(F_l) \parallel _ 2}$$k代表$F_l$中元素的个数，$\eta$则是一个超参数。有了这样的学习率调整，在每层中都能自动适应当层的情况进行学习率的调整。
算法流程描述
上面就是本篇论文提出的所有新东西与新设计，文章中也给出了加法网络前向和后向传播的流程描述
实验
实验数据和结果对比见原论文
一些想法
- 本论文还只是初步提出了一个idea以及初步进行了实验，实验内容也并不复杂，这个网络的稳定性和各个方面的性能有待进一步研究，但不失为一个非常好的思路。
- 本论文的目的就是打造一个计算更快的网络，但是实验结果没有给出这个网络所耗费的时间。
- 论文中有些公式的提出并没有给出特别明确的理由（也许我自己我没理解），如L1距离的公式为什么前面要带负号，以及自适应学习率的公式为什么是那样。