python数据分析个人学习读书笔记-目录索引
第7章探索了如何处理和理解时间序列数据,并建立ARMA模型以及ARIMA模型。注意:我在本章花的时间较长,主要是对dataframe结构不熟。
本章会介绍处理、分析和预测时间序列数据的各种技术。会学习以下技巧:
·在Python中如何处理日期对象
·理解时间序列数据
·平滑并转换观测值
·过滤时间序列数据
·移除趋势和季节性
·使用ARMA和ARIMA模型预测未来
7.1导论
时间序列随处可见;如果分析股票市场、太阳黑子,或河流,你就是在观察随时间延展的现象。数据科学家在职业生涯中处理时间序列数据总是不可避免的。本章中,我们会遇到对时间序列进行处理、分析和构建模型的多种技巧。
本章中用到的数据集来自网上河流的Web文档:http://ftp.uni-bayreuth.de/math/statlib/datasets/riverflow。这个文档本质上就是一个shell脚本,为本章创建数据集。要从文档中创建原始文件,你可以使用Windows下的Cygwin或者Mac/Linux下的Terminal,执行下述命令(假设你将文档保存在riverflows.webarchive):
/* sh riverflows.webarchive */
邀月建议:安装cygwin巨麻烦,还是用安装好的CentOS虚拟机执行一下。
7.2在Python中如何处理日期对象
时间序列是以某个时间间隔进行采样得到的数据,例如,记录每秒的车速。拿到这样的数据,我们可以轻松估算经过的距离(假设观测值加总并除以3600)或者汽车的加速度(计算两个观测值之间的差异)。可以直接用pandas处理时间序列数据。
准备:需装好pandas、NumPy和Matplotlib。
步骤:从Web文档开始,我们进行清理,并形成两个数据集:美国河(http://www.theameri-canriver.com)和哥伦比亚河(http://www.ecy.wa.gov/programs/wr/cwp/cwpfactmap.html)。用pandas读取时间序列数据集很简单(ts_handlingData.py文件):
1 import numpy as np 2 import pandas as pd 3 import pandas.tseries.offsets as ofst 4 import matplotlib 5 import matplotlib.pyplot as plt 6 7 # change the font size 8 matplotlib.rc('xtick', labelsize=9) 9 matplotlib.rc('ytick', labelsize=9) 10 matplotlib.rc('font', size=14) 11 12 # files we'll be working with 13 files=['american.csv', 'columbia.csv'] 14 15 # folder with data 16 data_folder = '../../Data/Chapter07/' 17 18 # colors 19 colors = ['#FF6600', '#000000', '#29407C', '#660000'] 20 21 # read the data 22 american = pd.read_csv(data_folder + files[0], 23 index_col=0, parse_dates=[0], 24 header=0, names=['','american_flow']) 25 26 columbia = pd.read_csv(data_folder + files[1], 27 index_col=0, parse_dates=[0], 28 header=0, names=['','columbia_flow']) 29 30 # combine the datasets 31 riverFlows = american.combine_first(columbia) 32 33 # periods aren't equal in the two datasets so find the overlap 34 # find the first month where the flow is missing for american 35 idx_american = riverFlows \ 36 .index[riverFlows['american_flow'].apply(np.isnan)].min() 37 38 # find the last month where the flow is missing for columbia 39 idx_columbia = riverFlows \ 40 .index[riverFlows['columbia_flow'].apply(np.isnan)].max() 41 42 # truncate the time series 43 riverFlows = riverFlows.truncate( 44 before=idx_columbia + ofst.DateOffset(months=1), 45 after=idx_american - ofst.DateOffset(months=1))
Tips:
/* Traceback (most recent call last): File "D:\Java2018\practicalDataAnalysis\Codes\Chapter07\ts_handlingData.py", line 49, ino.write(riverFlows.to_csv(ignore_index=True)) TypeError: to_csv() got an unexpected keyword argument 'ignore_index' D:\Java2018\practicalDataAnalysis\Codes\Chapter07\ts_handlingData.py:80: FutureWarning: how in .resample() is deprecated the new syntax is .resample(...).mean() year = riverFlows.resample('A', how='mean') */
解决方案:
/* # year = riverFlows.resample('A', how='mean') year = riverFlows.resample('A').mean() # o.write(riverFlows.to_csv(ignore_index=True)) o.write(riverFlows.to_csv(index=True)) */
原理:首先,我们引入所有必需的模块:pandas和NumPy。我们将得到两个文件:american.csv和columbia.csv。它们都位于data_folder。
我们使用已经熟悉的pandas的.read_csv(...)方法。先读入american.csv文件。指定index_col=0,让方法将第一列作为索引。要让pandas将某列当成日期处理,我们显式地命令.read_csv(...)方法将列作为日期解析(parse_dates)。
将两个文件合并成一个数据集。然后改动列名:我们告诉方法,这里没有头部,并且将自行提供名字。注意第一列不需要任何名字,它将被转换成索引。我们用同样的方式读入哥伦比亚河的数据。
读入两个文件后,将它们联系在一起。pandas的.combine_first(...)方法操作第一个数据集,插入哥伦比亚河数据集的列。
如果没有改变DataFrame的列名,.combine_first(...)方法将使用被调用DataFrame的数据来填充调用者DataFrame的空隙。
两个文件的时期不同,但是有重叠部分:美国河数据从1906年到1960年,哥伦比亚河数据从1933年到1969年。查看一下重叠的时期;我们连接的数据集只有1933年到1960年的数据。
首先,找到美国河没有数据的最早日期(american_flow列)。检查riverFlows的索引,选取american_flow值不是数字的所有日期;使用.apply(...)方法并使用NumPy的.isnan方法检查DataFrame的元素。做完这个之后,选取序列中的最小日期。
而对于columbia_flow,我们找的是没有数据的最晚日期。和处理美国河数据类似,我们先取出所有数据不是数字的日期,然后选取最大值。
.truncate(...)方法可以根据DatetimeIndex从DataFrame中移除数据。
DatetimeIndex是数字组成的不可变数组。内部由大整数表示,但看上去是日期-时间对象:既有日期部分也有时间部分的对象。
参考http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DatetimeIndex.html。
我们向.truncate(...)方法传递两个参数。before参数指定了要舍弃哪个日期之前的记录,after参数指定了保留数据的最后一个日期。
idx_...对象保存了至少有一列没有数据的日期的最小值和最大值。不过,如果将这些日期传入.truncate(...)方法,我们也会选出同样没有数据的极值点。应对这种情况,我们用.DateOffset(...)方法将日期移个位。我们只挪一个月。
如果想更深入了解.DateOffset(...)方法,可参考http://pandas.pydata.org/pandas-docs/stable/timeseries.html#dateoffset-objects。
最后将连接后的数据集保存到文件。(更多信息参考本书1.2节)
/* Index of riverFlows DatetimeIndex(['1933-01-31', '1933-02-28', '1933-03-31', '1933-04-30', '1933-05-31', '1933-06-30', '1933-07-31', '1933-08-31', '1933-09-30', '1933-10-31', ... '1960-03-31', '1960-04-30', '1960-05-31', '1960-06-30', '1960-07-31', '1960-08-31', '1960-09-30', '1960-10-31', '1960-11-30', '1960-12-31'], dtype='datetime64[ns]', name='', length=336, freq=None) csv_read['1933':'1934-06'] american_flow columbia_flow 1933-01-31 10.7887 24.10 1933-02-28 14.6115 20.81 1933-03-31 19.6236 22.96 1933-04-30 21.9739 37.66 1933-05-31 28.0054 118.93 1933-06-30 66.0632 331.31 1933-07-31 113.4373 399.27 1933-08-31 162.0007 250.89 1933-09-30 156.6771 116.10 1933-10-31 17.9246 69.38 1933-11-30 7.0792 52.95 1933-12-31 4.0493 40.21 1934-01-31 11.5816 35.40 1934-02-28 18.5192 28.88 1934-03-31 53.8586 33.41 1934-04-30 75.8608 102.22 1934-05-31 89.3963 259.67 1934-06-30 116.2973 390.77 Shifting one month forward american_flow columbia_flow 1933-02-28 10.7887 24.10 1933-03-31 14.6115 20.81 1933-04-30 19.6236 22.96 1933-05-31 21.9739 37.66 1933-06-30 28.0054 118.93 1933-07-31 66.0632 331.31 Shifting one year forward american_flow columbia_flow 1934-01-31 10.7887 24.10 1934-02-28 14.6115 20.81 1934-03-31 19.6236 22.96 1934-04-30 21.9739 37.66 1934-05-31 28.0054 118.93 1934-06-30 66.0632 331.31 Averaging by quarter american_flow columbia_flow 1933-03-31 15.007933 22.623333 1933-06-30 38.680833 162.633333 Averaging by half a year american_flow columbia_flow 1933-01-31 10.788700 24.100000 1933-07-31 43.952483 155.156667 Averaging by year american_flow columbia_flow 1933-12-31 51.852875 123.714167 1934-12-31 44.334742 128.226667 */
更多:从时间序列DataFrame中选取数据很直接:你仍然可以使用已知的DataFrame取子集的方法(比如,使用元素索引的riverFlows[0:10]或者.head(...)方法)。不过,有了DataFrame和DatetimeIndex索引,你也可以传日期:
print(riverFlows['1933':'1934-06'])
这行命令会打印出1933年到1934年6月的所有记录。注意,尽管有每月的数据,我们依然可以传入一个年份;pandas会选取相应的观测值。
有时候,你需要时间平移后的观测值,比如,测量仪的内部时钟没调整好,导致观测值偏了一小时,或者一个人为错误让观测值偏了一年。这可以用.shift(...)方法轻松纠正:
1 # shifting the data 2 by_month = riverFlows.shift(1, freq='M') 3 by_year = riverFlows.shift(12, freq='M')
传给.shift(...)方法的第一个参数指定了要偏移的数字,freq参数指定了频率(本例中是一个月)。
有时,你想在季末或年末时计算平均值(或总和)。可通过.resample(...)方法轻松做到:
1 # averaging by quarter 2 quarter = riverFlows.resample('Q').mean() 3 # averaging by half a year 4 half = riverFlows.resample('6M').mean() 5 # averaging by year 6 year = riverFlows.resample('A').mean()
第一个参数定义了频率:Q意味着季末(三月、六月、九月和十二月),how指定了怎么处理观测值(本例中使用mean,因为对我们的数据来说平均值比较有意义,但如果要处理销售额数据,你也许会指定sum)。
A是年末,6M是半年末,即十二月和六月。
另外,pandas可轻松绘制时间序列的图:
1 import matplotlib 2 import matplotlib.pyplot as plt 3 matplotlib.rc('font', size=14) 4 5 # colors 6 colors = ['#FF6600', '#000000', '#29407C', '#660000'] 7 8 # plot time series 9 # monthly time series 10 riverFlows.plot(title='Monthly river flows', color=colors) 11 plt.savefig(data_folder + '/charts/monthly_riverFlows.png', 12 dpi=300) 13 plt.close()
先引入Matplotlib模块,更改x轴和y轴的数字与标题。
Matplotlib的配置项可参考http://matplotlib.org/users/customizing.html。
然后指定颜色;这个常量在所有图表中都会用到。
.plot(...)方法绘图。我们定义标题,允许方法从颜色列表中挑选颜色。最后,将图保存到文件并关闭,以释放内存。
月度和季度图表如下:
查看月度图表,你也许会觉得两条河的流动没什么变化;而季度图则展示了不同之处:
理解时间序列数据
希望从数据集中看出什么时,一件基本事实是:如果不理解你要处理的数据,你不可能构建一个成功的统计模型。
准备:需装好pandas、Statsmodels和Matplotlib。
步骤:
处理时间序列的基本统计方法是ACF(autocorrelation function,自相关函数)、PACF(partial autocorrelation function,偏自相关函数)和谱密度(ts_timeSeriesFunctions.py文件):
1 # time series tools 2 import statsmodels.api as sm 3 4 # read the data 5 riverFlows = pd.read_csv(data_folder + 'combined_flow.csv', 6 index_col=0, parse_dates=[0]) 7 8 # autocorrelation function 9 acf = {} # to store the results 10 f = {} 11 12 for col in riverFlows.columns: 13 acf[col] = sm.tsa.stattools.acf(riverFlows[col]) 14 15 # partial autocorrelation function 16 pacf = {} 17 18 for col in riverFlows.columns: 19 pacf[col] = sm.tsa.stattools.pacf(riverFlows[col]) 20 21 # periodogram (spectral density) 22 sd = {} 23 24 for col in riverFlows.columns: 25 sd[col] = sm.tsa.stattools.periodogram(riverFlows[col])
原理:为了节省篇幅,我们这里省略了引入和声明变量的步骤。细节可查看源文件。
首先,以类似的方式读入(我们在之前的技巧里创建的)数据集,不过不指定变量的名字,而是用.read_csv(...)方法从文件的第一行获取。
然后计算ACF。ACF体现了t时刻的观测值与t+lag时刻的观测值的关联有多强,这里lag是时间间隔。在本书后续部分(使用ARMA和ARIMA模型预测未来),我们会使用ACF函数计算ARMA(或ARIMA)模型的MA(moving average,移动平均)。在这里用Statsmodels模型的.acf(...)方法计算时间序列的ACF值。.acf(...)方法的nlags参数,默认值是40,我们就用默认值。
在给定了以往延迟的条件下,PCAF可以看成是对当前观测值的回归。我们用PACF曲线得到ARMA(或ARIMA)模型的AR(auto-regressive,自回归)。使用Statsmodels模型的.pacf(...)方法计算时间序列的PACF值。
如果对ACF和PACF感兴趣的话,你可以参考https://onlinecourses.science.psu.edu/stat510/node/62。
最后计算周期图法,这个方法可以帮我们找到数据中的基础频率,即数据中波峰和波谷的主频率。
让我们来绘制该图:
1 # plot the data 2 fig, ax = plt.subplots(2, 3) # 2 rows and 3 columns 3 4 # set the size of the figure explicitly 5 fig.set_size_inches(12, 7) 6 7 # plot the charts for American 8 ax[0, 0].plot(acf['american_flow'], colors[0]) 9 ax[0, 1].plot(pacf['american_flow'],colors[1]) 10 ax[0, 2].plot(sd['american_flow'], colors[2]) 11 ax[0, 2].yaxis.tick_right() # shows the numbers on the right 12 13 # plot the charts for Columbia 14 ax[1, 0].plot(acf['columbia_flow'], colors[0]) 15 ax[1, 1].plot(pacf['columbia_flow'],colors[1]) 16 ax[1, 2].plot(sd['columbia_flow'], colors[2]) 17 ax[1, 2].yaxis.tick_right() 18 19 # set titles for columns 20 ax[0, 0].set_title('ACF') 21 ax[0, 1].set_title('PACF') 22 ax[0, 2].set_title('Spectral density') 23 24 # set titles for rows 25 ax[0, 0].set_ylabel('American') 26 ax[1, 0].set_ylabel('Columbia')
首先,我们创建了一个图表,将以两行三列的方式放6个子图。我们显式地指定图表的大小。
下面画图。ax是放坐标轴对象的NumPy数组;在我们的例子中,这是个二维数组。通过指定对象的坐标,我们指定图表的位置(0,0是左上角)。
行中的最后一个图表,我们通过调用.yaxis.tick_right()方法设置y轴的数字,展示在图表的右侧。
我们只在绘制ACF、PACF和谱密度时设定图表标题。对于行,我们指定y轴的标签,以区分不同的河流。
绘制出的图表如下: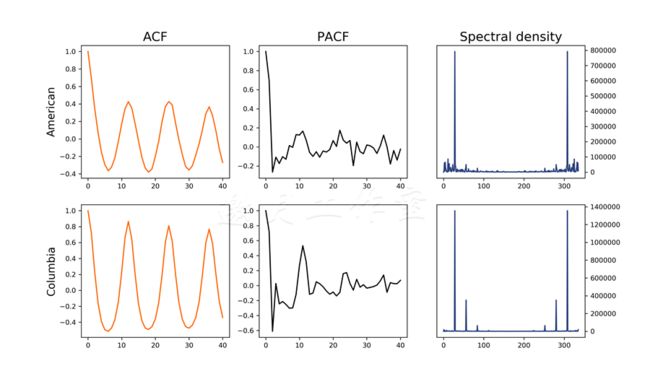
Tips:
你会发现ACF图表中有一个重复的模式。这暗示着我们的数据(如预期般)是周期性的(年度周期模式)。这也暗示着我们的处理过程是不平稳的。
平稳过程指的是,方差和联合概率不随时间变化(http://www.itl.nist.gov/div898/handbook/pmc/section4/pmc442.htm)。
PACF展示了,时刻t的观测值强烈依赖于时刻t-1和t-2的观测值(对更之前的快照依赖较少)。分析谱密度可知基础频率大约在29;即,每29个月会重复一个基本的模式。这出乎我们的意料,我们本以为序列重复的间隔会是12的倍数。这可能是多种因素的影响:错误记录的观测值,错误的设备,或者某些观测年发生的基本偏移模式。
更多:之前ACF和PACF的图表并不容易得到置信区间的主要偏差:这些偏差让我们很容易辨别出时间序列过程的AR和MA。
不过,Statsmodels提供了便捷的函数.plot_acf(...)和.plot_pacf(...)(ts_timeSeries Functions_alternative.py文件):
1 # plot the data 2 fig, ax = plt.subplots(2, 2, sharex=True) 3 4 # set the size of the figure explicitly 5 fig.set_size_inches(8, 7) 6 7 # plot the charts for american 8 sm.graphics.tsa.plot_acf( 9 riverFlows['american_flow'].squeeze(), 10 lags=40, ax=ax[0, 0]) 11 12 sm.graphics.tsa.plot_pacf( 13 riverFlows['american_flow'].squeeze(), 14 lags=40, ax=ax[0, 1]) 15 16 # plot the charts for columbia 17 sm.graphics.tsa.plot_acf( 18 riverFlows['columbia_flow'].squeeze(), 19 lags=40, ax=ax[1, 0]) 20 21 sm.graphics.tsa.plot_pacf( 22 riverFlows['columbia_flow'].squeeze(), 23 lags=40, ax=ax[1, 1]) 24 25 # set titles for rows 26 ax[0, 0].set_ylabel('American') 27 ax[1, 0].set_ylabel('Columbia')
首先创建图表,可容纳4个子图(放在2×2的网格上)。将sharex参数设置为True意味着图表的坐标轴对象有相同的时域。我们也显式指定图表大小。
.plot_acf(...)方法和.plot_pacf(...)方法都以用来绘图的数据作为第一个参数。.squeeze()方法将单列的DataFrame转换为一个序列对象。这里,我们显式指定时间间隔。ax参数指定了图表放置的位置。
7.4平滑并转换观测值
顾名思义,平滑数据就是移除数据中的噪音,使得图表更为平滑。
那你该这么做吗?从展示的角度说,当然!从建模的角度看,不是必需的——参考William Briggs在http://wmbriggs.com/post/195/的论述。
准备:需装好pandas、NumPy和Matplotlib。
步骤:本技巧中,我们将介绍如何计算移动平均和用对数函数转换数据(ts_smoothing.py文件):
1 ma_transform12 = pd.rolling_mean(riverFlows, window=12) 2 ma_transformExp = pd.ewma(riverFlows, span=3) 3 log_transfrom = riverFlows.apply(np.log)
原理:pandas的.rolling_mean(...)方法计算移动平均数。这个方法对时刻>t<与时刻>(t+window-1)<之间的观测值计算平均数,并用这个平均数替代时刻>t<的观测值。你也可以不取window-1个之前的观测值,而是指定center参数,这样会在时刻t两边取同样数目的观测值。
.ewma(...)方法使用一个指数衰减的函数来平滑数据。span参数控制影响窗口——计算加权平均时还有多少相关的观测值。
如果要更了解这些技巧,可以学习pandas的文档:http://pandas.pydata.org/pandas-docs/stable/computation.html#exponentially-weighted-moment-functions。
对数据做对数转换有利于计算,有时候转换后也能看出更多模式。和平滑不同,这是一个可逆的过程,所以我们不会损失精确度(只要你不做进一步的转换,比如,计算对数转换后的移动平均)。这里,我们使用NumPy库里的.log方法。它取用时刻t的观测值,和window-1个之前的观测值,计算其平均数,并用得到的值替换时刻t的观测值。
得到的图表展示了技巧将原始的数据集变得多么不同: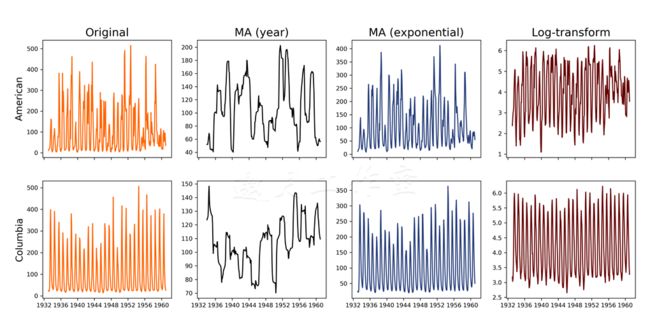
MA平滑技巧移除了很多噪音,揭示了数据中的局部趋势;对美国河而言,水位从开始到1942年左右是上升的,然后直到1950年都是下降的,之后又是有升有降。而对于哥伦比亚河,你可以看到一开始的下降趋势,1945年左右才翻转过来。
指数平滑不像MA这么天然,它只移除数据中最大的波峰,同时保留其整体形状。log变换将数据的幅度正规化。前面提到过,这是唯一一个完全可逆的技巧,不用担心数据丢失。
更多:Holt变换是另一个指数平滑的例子。区别在于它不对smoothing参数取幂(ts_smoothing_alternative.py文件):
1 import pandas as pd 2 import numpy as np 3 4 def holt_transform(column, alpha): 5 ''' 6 Method to apply Holt transform 7 8 The transform is given as 9 y(t) = alpha * x(t) + (1-alpha) y(t-1) 10 ''' 11 # create an np.array from the column 12 original = np.array(column) 13 14 # starting point for the transformation 15 transformed = [original[0]] 16 17 # apply the transform to the rest of the data 18 for i in range(1, len(original)): 19 transformed.append( 20 original[i] * alpha + 21 (1-alpha) * transformed[-1]) 22 23 return transformed
平滑后时刻t的值由其观测值与之前平滑后的值决定;每个观测值的影响由alpha参数控制。
我们先创建一个NumPy数组。变换的起点是初始的观测值。然后遍历数组中所有的观测值,应用处理逻辑。
这里使用Holt平滑法,alpha设为0.5:
# transformations ma_transformHolt = riverFlows.apply( lambda col: holt_transform(col, 0.5), axis=0)
axis设为0时,.apply(...)方法将列逐一传入holt_transform(...)方法。
我们也可以进行差分处理,这样可快速移除数据的趋势,使其稳定;差分是计算时刻t及其前导(时刻t-1)观测值之差的方法:
difference = riverFlows - riverFlows.shift()
这里,我们使用了之前在7.2节中解释过的.shift(...)方法。
得到的变换如下所示:
真心赞一个!
可以看出,如同指数平滑一样,这个方法也移除了大部分噪音,但保留了数据的形状。如果相比于时间序列中的值本身,你更关心预测变化,那么差分是很有用的;预测股市变化就是一个应用场景。
7.5过滤时间序列数据
通过平滑移除噪音只是技巧之一。本技巧中,我们看看如何通过卷积及其他滤波器从数据中提取某些频率。
准备:需装好pandas、Statsmodels、NumPy、Scipy和Matplotlib。
步骤:
简单来说,卷积就是f函数(我们的时间序列)和g函数(我们的滤波器)的交叠。卷积模糊了时间序列(从这个角度,也可以将其看成一个平滑技巧)。
这里有一个不错的对卷积的介绍:http://www.songho.ca/dsp/convolution/convolution.html。
下面的代码在ts_filtering.py中:
1 # prepare different filters准备不同的滤波器 2 MA_filter = [1] * 12 3 linear_filter = [d * (1 / 12) for d in range(0, 13)] 4 gaussian = [0] * 6 + list(sc.signal.gaussian(13, 2)[:7]) 5 6 # convolve卷积 7 conv_ma = riverFlows.apply( 8 lambda col: sm.tsa.filters.convolution_filter( 9 col, MA_filter), axis=0).dropna() 10 11 conv_linear = riverFlows.apply( 12 lambda col: sm.tsa.filters.convolution_filter( 13 col, linear_filter), axis=0).dropna() 14 15 conv_gauss = riverFlows.apply( 16 lambda col: sm.tsa.filters.convolution_filter( 17 col, gaussian), axis=0).dropna()
原理:
第一个滤波器,我们通过卷积可以实现一个移动平均(MA)滤波器:这个滤波器是由12个元素组成的列表,每个元素都是1。
第二个滤波器在12个周期内线性增长;这个滤波器逐步降低输出值中旧观测值的重要性。
最后一个滤波器使用高斯函数过滤数据。
这些滤波器的响应看上去像这样: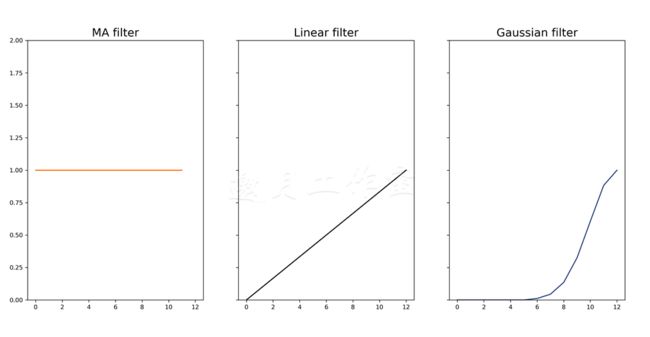
我们使用Statsmodels的.convolution_filter(...)方法过滤数据集。这个方法将数据作为第一个参数及过滤数组。
对有些观测值,方法本身并不能为其生成任何结果,所以我们使用.dropna()移除缺失的观测值。过滤后的数据集如下所示: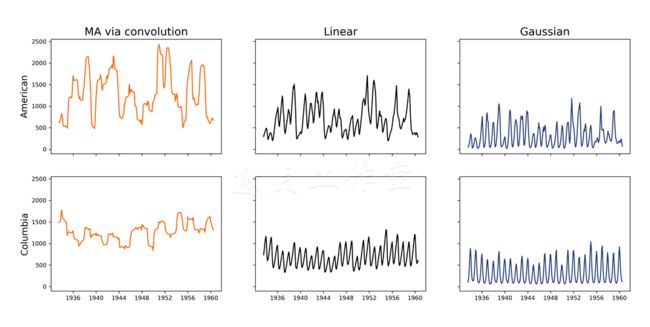
通过卷积的MA产生了和之前的.rolling_mean(...)方法同样的结果。线性滤波器从数据集中移除波峰。最后,高斯模糊不仅减少了观测值的幅度,而且让其更平滑。
更多:对于经济数据(或者像我们的例子,自然中的数据),某些滤波器会更合适:比如BK(Baxter-King)、HP(Hodrick-Prescott)与CF(Christiano-Fitzgerald)。
如果有兴趣,可以查看相关的学术论文:http://www.nber.org/papers/w5022.pdf(Baxter-King),
https://www0.gsb.columbia.edu/faculty/rhodrick/prescott-hodrick1997.pdf(Hodrick-Prescott)
与http://www.nber.org/papers/w7257.pdf(Christiano-Fitzgerald)。
我们使用Statsmodels实现这些滤波器:
bkfilter = sm.tsa.filters.bkfilter(riverFlows, 18, 96, 12) hpcycle, hptrend = sm.tsa.filters.hpfilter(riverFlows, 129600) cfcycle, cftrend = sm.tsa.filters.cffilter(riverFlows, 18, 96, False)
BK过滤器是一个带通滤波器;从时间序列中移除高频和低频。.bkfilter(...)方法以数据作为第一个参数。下一个参数是振动的最小周期;对于月度数据,推荐使用18,季度推荐使用6,年度推荐使用1.5。下一个参数定义了振动的最大周期:对于月度数据,推荐使用96。最后一个参数决定了滤波器的超前-滞后(或者说,一个窗口)。
HP过滤器通过解决一个最小化问题,将初始的时间序列拆成趋势和业务周期组件。.hpfilter(...)方法以数据作为第一个参数及平滑的参数。通常,对季度数据使用1600作为频率,年度数据使用6.25,月度数据(即本例中)使用129600。
CF过滤器将初始的时间序列拆成趋势和业务周期组件,在这个意义上来说,和HP过滤器类似。.cffilter(...)也是以数据作为第一个参数。与BK过滤器类似,接下来两个参数指定了振动的最小周期和最大周期。最后一个参数drift指定了是否要从数据中移除趋势。
过滤后的数据如下: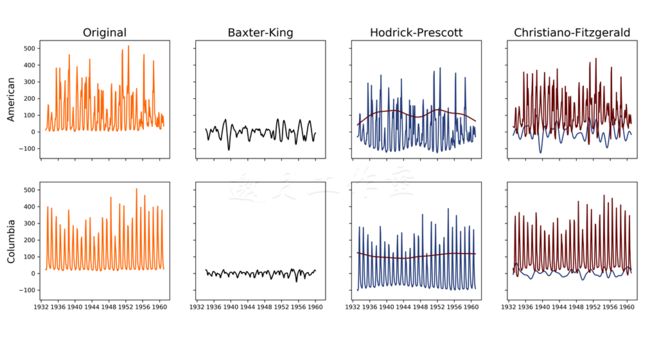
BK过滤器从数据中移除幅度,并使其静止。分析HP过滤器的输出可以看出,哥伦比亚河的长期趋势几乎是恒定的,而美国河的趋势一直在变。美国河的周期组件也体现了类似的模式。CF过滤器的输出证明了这一点:美国河的趋势组件比哥伦比亚河的更多变。
7.6移除趋势和季节性
如同之前提到的,时间序列是平稳的等价条件,并且其平均值、方差和自相关都不随时间变化。这意味着,有趋势和季节性的时间过程就是不平稳的。
下一个技巧要介绍的ARMA模型和ARIMA模型要求数据是平稳的(或接近平稳)。所以,本技巧中,我们学习如何从河水流动数据中移除趋势和季节性。
准备:需装好pandas、NumPy、Statsmodels和Matplotlib。
步骤:Statsmodels提供了方便的移除趋势和季节性的方法(ts_detrendAndRemoveSeasonality.py文件):
1 import pandas as pd 2 import numpy as np 3 import matplotlib 4 import matplotlib.pyplot as plt 5 6 # change the font size 7 matplotlib.rc('xtick', labelsize=9) 8 matplotlib.rc('ytick', labelsize=9) 9 matplotlib.rc('font', size=14) 10 11 # time series tools 12 import statsmodels.api as sm 13 14 def period_mean(data, freq): 15 ''' 16 Method to calculate mean for each frequency 17 ''' 18 return np.array( 19 [np.mean(data[i::freq]) for i in range(freq)]) 20 21 # folder with data 22 data_folder = '../../Data/Chapter07/' 23 24 # colors 25 colors = ['#FF6600', '#000000', '#29407C', '#660000'] 26 27 # read the data 28 # riverFlows = pd.read_csv(data_folder + 'combined_flow.csv', 29 # index_col=0, parse_dates=[0]) 30 riverFlows = pd.read_csv(data_folder + 'combined_flow.csv') 31 32 33 # detrend the data 34 detrended = sm.tsa.tsatools.detrend(riverFlows, 35 order=1, axis=0) 36 37 # create a data frame with the detrended data 38 detrended = pd.DataFrame(detrended, index=riverFlows.index, 39 columns=['american_flow_d', 'columbia_flow_d']) 40 41 # join to the main dataset 42 riverFlows = riverFlows.join(detrended) 43 44 # calculate trend 45 riverFlows['american_flow_t'] = riverFlows['american_flow'] \ 46 - riverFlows['american_flow_d'] 47 riverFlows['columbia_flow_t'] = riverFlows['columbia_flow'] \ 48 - riverFlows['columbia_flow_d'] 49 50 # number of observations and frequency of seasonal component 51 nobs = len(riverFlows) 52 freq = 12 # yearly seasonality 53 54 # remove the seasonality 55 for col in ['american_flow_d', 'columbia_flow_d']: 56 period_averages = period_mean(riverFlows[col], freq) 57 riverFlows[col[:-2]+'_s'] = np.tile(period_averages, 58 nobs // freq + 1)[:nobs] 59 riverFlows[col[:-2]+'_r'] = np.array(riverFlows[col]) \ 60 - np.array(riverFlows[col[:-2]+'_s'])
原理:首先,我们读入数据。
使用Statsmodels的.detrend(...)方法,我们从数据中移除趋势。order参数指定了趋势的类型:0代表常数,1代表趋势是线性的,2代表要移除的是一个二次趋势。
.detrend(...)方法返回一个NumPy数组;在我们的例子中,这是一个二维数组,因为初始的数据集中有两列。所以,为了便于加入初始数据集,下一步我们用移除趋势的数据创建一个DataFrame。我们重用了初始DataFrame的索引:riverFlows。而且,为了避免和初始数据集冲突,列名加上后缀_d。
pandas的.join(...)方法(默认情况下)根据索引合并两个DataFrame:匹配两个DataFrame的索引,返回对应的值。不过,.join(...)方法给你控制权,允许你指定要连接到的列;键-列在两个数据集中都要有。它也允许你指定如何连接DataFrame:默认情况下,这是个左连接,从调用方DataFrame的每行记录出发,连接传入DataFrame中键名匹配的所有值;由于两个DataFrame中索引相同,我们只需要调用这个方法即可。
要理解其他类型的连接,参考http://www.sql-join.com。原作者也推荐查看.join(...)方法的文档:http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.join.html。
得到的时间序列和初始的并没有太大差别:
/* 错,生成空白!!!! */
解决方案:
/* # create a data frame with the detrended data #用移除趋势的数据创建一个DateFrame # detrended = pd.DataFrame(detrended, index=riverFlows.index, # columns=['american_flow_d', 'columbia_flow_d']) #原方法中列'american_flow_d', 'columbia_flow_d'都是NaN detrended.rename(columns={'american_flow':'american_flow_d', 'columbia_flow':'columbia_flow_d'}, inplace = True) */
趋势就是初始值与去趋势化之后的值之间的差别。
去趋势化时间序列之后,我们可以计算季节性组件。我们期望得到的是一个年度季节性,所以freq被设为12。这意味着我们期望每12个月会重复一个模式。period_mean(...)方法就是计算这个的。data[i::freq]选取第i个观测值,并在第i个之后,每隔12个(freq)选取观测值,动态创建列表。
子集语法d[f:l:freq]指定了第一个位置f,最后一个位置l,以及取样的频率freq。假设d=[1,2,3,4,5,6,7,8,9,10]和d[1::2],我们会得到[2,4,6,8,10]。
NumPy的.mean(...)方法计算数组中所有元素的平均值。对于每条河流,我们得到下面的结果: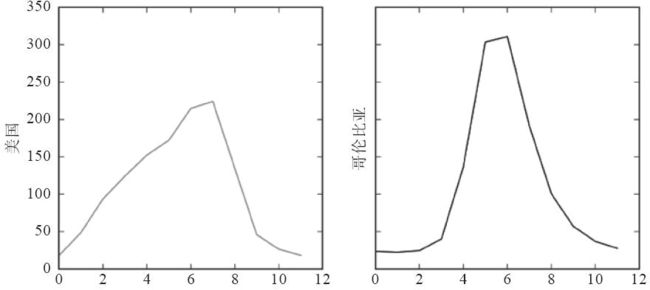
美国河看起来更柔顺:八月份左右逐渐涨到顶峰,然后越到年末越回落。相反,哥伦比亚河一年中大部分都很平静,到夏季突然涨得厉害。
计算了季节性的平均,我们可以从去趋势化后的数据中提取出来。我们使用NumPy的.tile(...)方法针对时间序列的长度重复季节模式。这个方法以要重复的模式作为第一个参数。第二个参数指定模式要重复多少次。
//操作符做的是整数除法,将得到的商圆整到最近的整数。
最后,我们计算移除季节性后的残差:
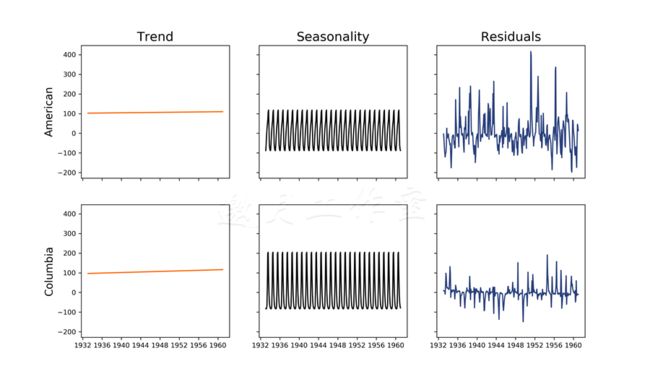
这里,我们将时间序列分解成一个线性趋势、季节性组件以及残差。可以看出,两条河的流量都随着时间增长,但是增长可忽略。我们可以清楚地看出(期望中的)年度模式,哥伦比亚河的方差更大。对于残差,美国河变化的幅度要显著高于哥伦比亚河。
更多:
Statsmodels有另一个分解时间序列的有用方法:.seasonal_decompose(...)。
不幸的是,Statsmodels的文档是缺失的;项目只在发布笔记中提到了.seasonal_decompose(...)方法,举了一个例子,而文档是找不到的。学习GitHub上的源代码,可以发现更多内容,作者推荐你也这么做(https://github.com/statsmodels/statsmodels/blob/master/statsmodels/tsa/seasonal.py。
这个方法以要分解的数据作为第一个参数。你可以指定基础模型的类型:可加的(我们的例子)或可乘的(传入m)。你也可以指定freq参数;这个参数可不传,频率也能通过数据推断出。
关于可加和可乘的分解模型的区别,推荐阅读https://onlinecourses.science.psu.edu/stat510/node/69。
方法返回一个DecomposeResult对象。要访问分解的组件,可调用对象的属性(ts_seasonalDecomposition.py):
1 for col in riverFlows.columns: 2 # seasonal decomposition of the data 3 sd = sm.tsa.seasonal_decompose(riverFlows[col], 4 model='a', freq=12) 5 6 riverFlows[col + '_resid'] = sd.resid \ 7 .fillna(np.mean(sd.resid)) 8 9 riverFlows[col + '_trend'] = sd.trend \ 10 .fillna(np.mean(sd.trend)) 11 12 riverFlows[col + '_seas'] = sd.seasonal \ 13 .fillna(np.mean(sd.seasonal))
得到的分解和之前得到的看上去不同:
差异来自于移除趋势的方式不同:我们假设趋势在整个时域上是线性的,而.seasonal_decompose(...)方法使用卷积滤波以发现基础趋势。仔细观察的话,你会发现这个趋势图和过滤时间序列数据中的MA图的相似之处;区别在于.seasonal_decompose(...)方法使用的权重。
7.7使用ARMA和ARIMA模型预测未来
ARMA(autoregressive moving average,自回归移动平均)模型及其泛化——ARIMA(autoregressive integrated moving average,差分自回归移动平均)模型——是从时间序列预测未来时常用的两个模型。ARIMA的泛化是指这是一个整体:模型的第一步是在估算AR和MA之前做差分。
准备:需装好pandas、NumPy、Statsmodels和Matplotlib。你还需要前面技巧里准备的数据。
步骤:我们将处理过程包装在方法里,以便大部分建模可以自动化(ts_arima.py文件):
1 def plot_functions(data, name): 2 ''' 3 Method to plot the ACF and PACF functions 4 ''' 5 # create the figure 6 fig, ax = plt.subplots(2) 7 8 # plot the functions 9 sm.graphics.tsa.plot_acf(data, lags=18, ax=ax[0]) 10 sm.graphics.tsa.plot_pacf(data, lags=18, ax=ax[1]) 11 12 # set titles for charts 13 ax[0].set_title(name.split('_')[-1]) 14 ax[1].set_title('') 15 16 # set titles for rows 17 ax[0].set_ylabel('ACF') 18 ax[1].set_ylabel('PACF') 19 20 # save the figure 21 plt.savefig(data_folder+'/charts/'+name+'.png', 22 dpi=300) 23 24 def fit_model(data, params, modelType, f, t): 25 ''' 26 Wrapper method to fit and plot the model 27 ''' 28 # create the model object 29 model = sm.tsa.ARIMA(data, params) 30 31 # fit the model 32 model_res = model.fit(maxiter=600, trend='nc', 33 start_params=[.1] * (params[0]+params[2]), tol=1e-06) 34 35 # create figure 36 fig, ax = plt.subplots(1, figsize=(12, 8)) 37 38 e = model.geterrors(model_res.params) 39 ax.plot(e, colors[3]) 40 41 chartText = '{0}: ({1}, {2}, {3})'.format( 42 modelType.split('_')[0], params[0], 43 params[1], params[2]) 44 45 # and put it on the chart 46 ax.text(0.1, 0.95, chartText, transform=ax.transAxes) 47 48 # and save the figure 49 plt.savefig(data_folder+'/charts/'+modelType+'_errors.png', 50 dpi=300) 51 52 53 # plot the model 54 plot_model(data['1950':], model_res, params, 55 modelType, f, t) 56 57 # and save the figure 58 plt.savefig(data_folder+'/charts/'+modelType+'.png', 59 dpi=300) 60 61 def plot_model(data, model, params, modelType, f, t): 62 ''' 63 Method to plot the predictions of the model 64 ''' 65 # create figure 66 fig, ax = plt.subplots(1, figsize=(12, 8)) 67 68 # plot the data 69 data.plot(ax=ax, color=colors[0]) 70 71 # plot the forecast 72 model.plot_predict(f, t, ax=ax, plot_insample=False) 73 74 # define chart text 75 chartText = '{0}: ({1}, {2}, {3})'.format( 76 modelType.split('_')[0], params[0], 77 params[1], params[2]) 78 79 # and put it on the chart 80 ax.text(0.1, 0.95, chartText, transform=ax.transAxes)
原理:读入数据后,我们首先查看残差的ACF和PACF函数:
1 #plot the ACF and PACF functions 2 plot_functions(riverFlows['american_flow_r'], 3 'ACF_PACF_American') 4 plot_functions(riverFlows['columbia_flow_r'], 5 'ACF_PACF_Columbia')
分析图表有助于我们决定模型的AR和MA组件:
前一张图和下一张图分别代表美国河和哥伦比亚河的ACF和PACF函数: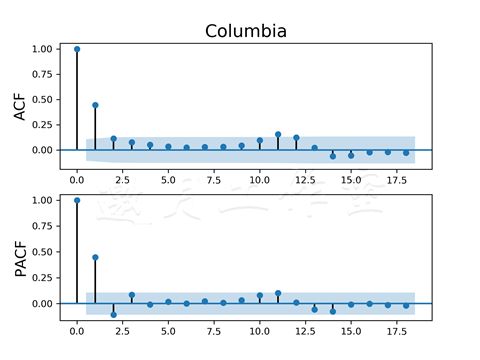
plot_functions(...)方法很像我们在7.3节中写的代码,所以这里我们不讨论它。
查看图表,我们可以看到自回归组件和移动平均组件,继而可以在模型构建阶段用其作为起始点:ACF函数有助于决定MA的顺序,而PACF函数允许我们决定AR部分。首要规则是查看显著落在置信区间之外的观测值。
从图表中可以推断:对于美国河模型我们以AR(2)和MA(4)开始,而对哥伦比亚河模型,我们从AR(3)和MA(2)开始:
1 # fit american models 2 fit_model(riverFlows['american_flow_r'], (2, 0, 4), 3 'ARMA_American', '1960-11-30', '1962') 4 fit_model(riverFlows['american_flow_r'], (2, 1, 4), 5 'ARIMA_American', '1960-11-30', '1962') 6 7 # fit colum models 8 fit_model(riverFlows['columbia_flow_r'], (3, 0, 2), 9 'ARMA_Columbia', '1960-09-30', '1962') 10 fit_model(riverFlows['columbia_flow_r'], (3, 1, 2), 11 'ARIMA_Columbia', '1960-09-30', '1962')
fit_model(...)方法封装了模型构建需要的所有步骤。它以要估算模型的数据作为第一个参数。params参数用于定义模型的参数。modelType参数用于在我们调用plot_model(...)方法时装饰图表;f(从)参数和t(到)参数也传给了plot_model(...)方法。
首先,我们创建模型对象。我们选择.ARIMA(...)模型,因为它可以特化为ARMA模型。.ARIMA(...)方法以数据作为第一个参数,以参数元组作为第二个参数。元组的第一个元素描述了模型的AR部分,第二个元素描述了(ARIMA模型中)用于差分的滞后,最后一个元素描述了MA组件。
将差分部分设为0,ARIMA模型就成了ARMA模型。
然后,我们调整模型。我们将循环的最大次数设为300,趋势不带常量。我们也定义start_params;以一个六元素的列表,所有AR与MR组件的和开始。列表中每个元素都设成了起始点0.1。容忍度设为0.000001;如果循环间误差的差别小于容忍度,就停止估算。
估算出模型后,我们看一下它是如何完成的。plot_model(...)方法绘制观测的数据。从图表的简明考虑,我们调用方法时限制数据从1950开始。.plot_predict(...)方法使用估算的模型参数预测未来的观测值。头两个参数指定预测的上下界限:我们可以选择起始点与结束点。我们将plot_insample设为False;这个参数的文档极为缺乏,我们就经验主义一把,认为这个参数避免了方法用不同的颜色画与预测交叠的观测值。
不要预测太远的未来,因为预测的置信区间没理由就会变宽。
我们在图表的左上角加上文字;用.text(...)方法做到这一点。头两个参数是图表上的坐标:用.transformAxes转换轴坐标,我们知道坐标(0,0)是左下角,(1,1)是右上角。第三个参数是希望加的文字。
估算出了模型,看下图表: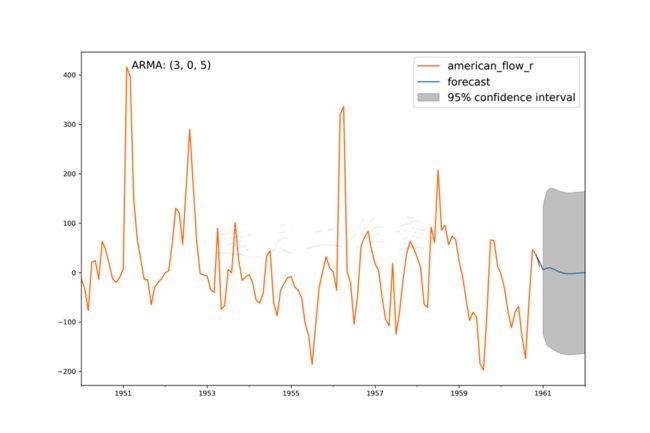
预测的美国河流量一开始遵循一个短期趋势,但是接下来(由于我们要从最后一个观测值往前走更远),置信区间激增,预测值就成了一个常数: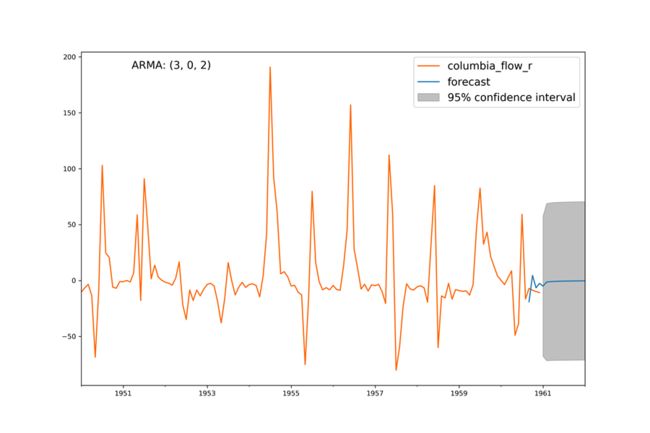
对于哥伦比亚河,一开始预测的流量看上去偏离了观测值,但是很快就平坦了: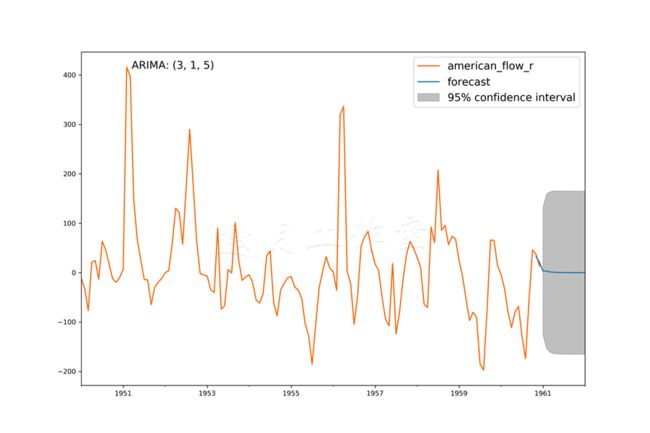
ARIMA模型的预测和ARMA模型的相差不大;预测一开始遵循观测数据,后来平坦了: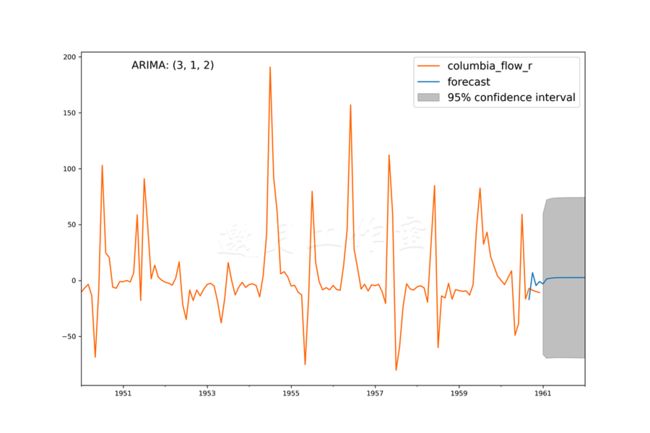
模型本质上是预测了残差的均值。
查看John Wittenauer对标普500指数的预测,可明白预测时间序列不是一件小事(http://www.johnwittenauer.net/a-simple-time-series-analysis-of-the-sp-500-index/)。
ACF和PACF函数得到的AR和MA参数应该只用作起始点。如果模型表现很好,就保留。否则,你可以微调。
我们也应该查看模型误差项的分布: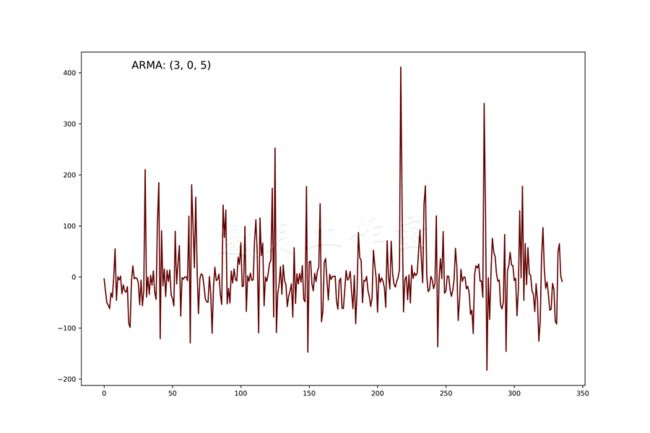
美国河的ARMA模型的误差项看上去很随机,这是预测时间序列时我们要追求的: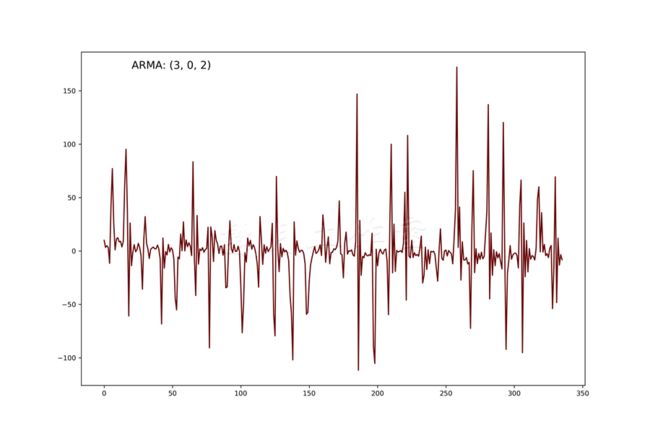
对于哥伦比亚河,误差项能看到一些重复的模式,这给模型预测未来流量的能力打上了一个问号: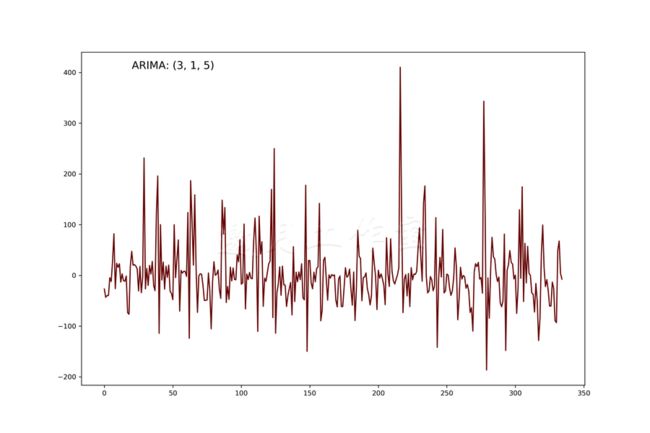
美国河的ARIMA模型也生成了类似随机残差的结果: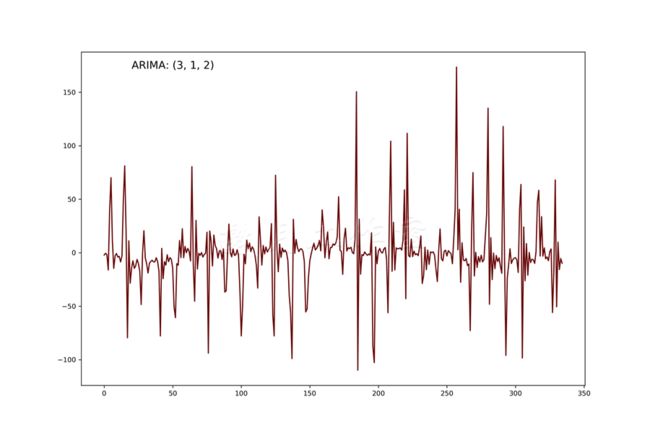
最终,误差项看上去应该像是白噪音。对于哥伦比亚河模型,这不一定对,因为我们也看到出现了模式。你可以试试不同的AR和MA参数,看模型是否有不同的结果。
参考
McKinney、Perktold和Seabold对时间序列做出了一个很好的展示/教程。值得一看:http://conference.scipy.org/scipy2011/slides/mckinney_time_series.pdf。
第7章完。
python数据分析个人学习读书笔记-目录索引
随书源码官方下载:
http://www.hzcourse.com/web/refbook/detail/7821/92