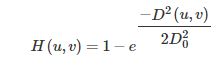1、频率滤波
图像的空间域滤波:用各种模板直接与图像进行卷积运算,实现对图像的处理,这种方法直接对图像空间操作,操作简单。图像处理不仅可以在空间域进行还可以在频率域进行,把空间域的图像开窗卷积形式,变换得到频率域的矩阵点乘形式得到比较好的效果。图像频域滤波,先把图像转换到频域空间,然后对不同的频率点进行滤波,使用信号处理的技术,对图像实现滤波。比如实现图像的轮廓提取,在空间域滤波中我们使用一个拉普拉斯模板就可以提取,而在频域内,我们使用一个高通滤波模板,可以实现轮廓的提取。
图像特征与像素点数值的关系:
图像尺寸418*564,如果把每一行所有像素,一行564个点的灰度作为一维向量画图,取前三行画成三条曲线,就得到了下面的图形。
subplot(2,1,1); imshow(img), title('原始图像'); line1 = img(1, :); line2 = img(2, :); line3 = img(3, :); subplot(2,1,2); hold on plot(line1, 'r'); plot(line2, 'g'); plot(line3, 'b');
输出结果如下图。
图像前几行的特征如下图(为了方便观察提取了不止三行):
![]()
从图像矩阵前几行的像素特征可见,图像平坦的地方像素曲线也平坦,图像亮的地方就是图像像素剧烈变化的地方,图像像素值发生较大差异的地方也是图像发生突变的地方,这些位置一般就是图像轮廓。图像的频率体现了图像中灰度变化剧烈程度,是灰度在平面空间上的梯度。所以前面讲的空域滤波,可以使用平滑来滤除噪声实现平滑,从上面曲线图像上看,可以按照信号处理思想来理解,平滑滤波就是频率低通。对应的,频率高通滤波就是空域的提取边界。
2、图像傅里叶变换
傅里叶变换可以将一个时域信号转换成在不同频率下对应的振幅及相位,其频谱就是时域信号在频域下的表现,而反傅里叶变换可以将频谱再转换回时域的信号。
imgPath = 'E:\opencv_pic\src_pic\pic4.bmp'; img = imread(imgPath); img=rgb2gray(img); f=fft2(im2double(img)); %FFT F=f; %FFT频谱 T=log(F+1); %频谱对数变换 subplot(1,2,1),imshow(img),title('原始图像'); subplot(1,2,2),imshow(T,[]),title('原始图像其频谱图');
输出结果如下,幅度图在四个角出现亮光。因为实信号以fs为采样速率的信号在 fs/2处混叠,所以实信号fft的结果中前半部分对应[0, fs/2],后半部分对应[ -fs/2, 0]。横向和纵向都需要把频率转换到[ -fs/2, fs/2]的区间,可以使用fftshift函数。
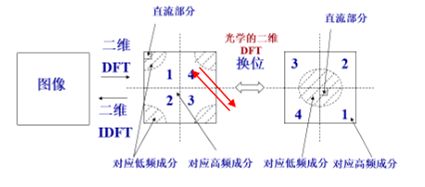
在数字图像处理中,常常需要将F(u,v)的原点移到N*N频域的中心,以便能清楚地分析傅里叶谱的情况,平移前空域、频域原点均在左上方。而fftshift的作用就是这样,将0频谱移到正中心。
Y = fftshift(X) 通过将零频分量移动到数组中心,重新排列傅里叶变换 X。
如果 X 是向量,则 fftshift 会将 X 的左右两半部分进行交换。
如果 X 是矩阵,则 fftshift 会将 X 的第一象限与第三象限交换,将第二象限与第四象限交换。
如果 X 是多维数组,则 fftshift 会沿每个维度交换 X 的半空间。
a =
1 2 3 4
6 7 8 9
>> fftshift(a)
ans =
8 9 6 7
3 4 1 2
平移后的图:
傅里叶变换的能量集中在频率很小的圆内,当D0增大时能量衰减很快,高频部分虽然携带的能量很少,但是包含丰富的边界和细节信息,所以当截止频率D0变小时,虽然亮度足够(因能量损失不大),但图像变模糊。
3、频域滤波
傅里叶变换可以把图像从空域变换到频域,而傅里叶反变换可以将图像的频谱变换为空域图像。可以利用图像空域和频域之间的对应关系,尝试将空域卷积滤波变换为频域滤波,而后再将频域滤波处理后的图像反变换回空间域,从而达到图像增强的目的。
G=imnoise(img,'gaussian', 0, 0.05);%模拟均值为0方差为0.05的高斯噪声, H=fft2(im2double(G)); %FFT H=fftshift(H); %FFT频谱平移 T=log(abs(H)); %频谱对数变换 subplot(2,2,1), imshow(G),title('添加高斯噪声图像'); subplot(2,2,2),imshow(T, []),title('频谱图');
使用傅里叶变换得到图像的频域幅度,应用傅里叶反变换得到空域图像.
img2 = (ifft2(ifftshift(H))); %===频域的图反变换到空域 img3 = im2uint8(mat2gray(img2)); %===取其灰度图 subplot(2,2,3),imshow(img3); title('anti-Fourier');
反变换效果如下图。
那么就可以在频率对图像进行滤波,然后反变换回空域就得到滤波后的图像。频率图可见在图像中心,是频率为0位置,所以如果限定只有低频通过则为低通,如果抑制频谱图中心位置,则是高通。可见图像在频域滤波是非常直观的。
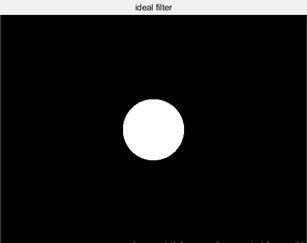
1)低通滤波器:
其中D(u,v)为频率域上(u,v)点到中心的距离,D0由自己设置.
2)高通滤波器:
高通滤波器同低通滤波器非常类似,只不过二者通过的波正好是相反的.
3)高斯低通滤波
4)高斯高通滤波
高斯频率低通滤波:
S=fftshift(fft2(G)); %G是添加高斯噪声的图像 [M,N]=size(S); d0=5; %GLPF滤波,d0=5,15,30 n1=floor(M/2); n2=floor(N/2); for i=1:M for j=1:N d=sqrt((i-n1)^2+(j-n2)^2); h=1*exp(-1/2*(d^2/d0^2)); S(i,j)=h*S(i,j); end end S=ifftshift(S); S=uint8(ifft2(S)); subplot(2,2,4),imshow(S),title('高斯低通滤波图像');
输出图像如下:
高斯滤波函数标准差变大,则高斯函数的傅里叶变换图像频率范围变宽,允许通过的频率范围变大,对应空域允许通过的图像变换更加多,可以允许的噪声更多。相反,如果标准差变小,频域范围变窄,允许通过的频率范围变小,对应空域对低频要求更加严格被抑制的高频更多,所以图像更加平滑,可能出现模糊现象。下面展示了不同的σ标准差情况下的滤波效果。
改为高通滤波,结果如下图:
对原图进行高斯高通滤波:
5、参考文献:
1、《数字图像处理与机器视觉》
第二版。 张铮、徐超、任淑霞、韩海玲等编著。
2、傅里叶变换在图像处理中的应用
https://www.cnblogs.com/Lynn0101/p/9892469.html
3、fftshift
https://ww2.mathworks.cn/help/matlab/ref/fftshift.html
个人博客,转载请注明。
https://www.cnblogs.com/pingwen/p/12442257.html