零知识证明中的超级新星:zk-SNARKs
什么是zk-SNARKs
zk-SNARK是“Zero-Knowledge Succinct Non-Interactive Argument ofKnowledge”的简称,指一种可以证明某人拥有某些信息的证明结构,例如:一把密码钥匙,没有显示该信息,也没有验证者和校验者之间的任何关系。
还是不知所云,“零知识”证明允许一方(证明方)向另一方(验证方)证明一项声明是真实的,而不披露除声明本身的有效性之外的任何信息。例如,给定一个随机数的hash,证明方可以使验证方相信确实存在一个具有这个hash值的数字,而不需要说明数字是什么。
在一个零知识的“知识证明”中,验证者不仅可以使验证者相信这个数字的存在,而且还可以使验证者相信他们实际上知道这个数字——同样,没有透露任何关于这个数字的信息。“证明”和“论证”之间的区别是相当技术性的,我们在这里不深入讨论。
“简洁”的零知识证明可以在几毫秒内得到验证,即使是关于非常大的项目的语句,其证明长度也只有几百字节。在第一代零知识协议中,证明方和验证方必须进行来回通信,但在“非交互式”结构中,证明仅仅包含了从证明方发送到验证方的单个消息。目前,要生成非交互式的、足够短的、可以发布到区块链的零知识证明,惟一已知的方法是初始设置阶段,该阶段生成验证程序和验证程序之间共享的公共引用字符串。我们将这个公共引用字符串作为系统的公共参数。
零知识非交互式证明
- 首先要理解什么是零知识,举一个非常简单的例子,一看就明白。
上图中数独,一个人填上谜面(Constraint)。然后证明给另外一个人说,这个数独是可解的。但又不能把底牌直接给对方看,这就是零知识。
那如何证明呢?
直接告诉对方说,你按照行和列,按照九宫格随便选,然后我将选出的放到九个麻袋,然后拿出来一看如下图。
如果对方不相信,那就多来几次,甚至可以全部尝试一次,在概率上100%证明。
- 然后要理解什么是非交互式。
上面两个人不断进行猜测证明的过程就是交互的过程。如果直接将交互过程都省掉,还能证明,那就是非交互式的零知识证明了。
那如何去掉交互过程呢?
发明一台零知识数独非交互式证明机(zk-SNIPM)。
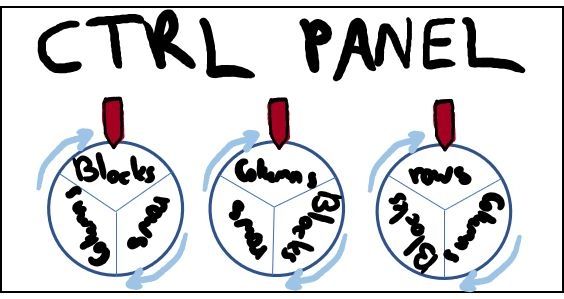
这台牛批的机器将上面的交互都自动化,这台机器有一个控制面板,里面有一串旋钮,用来每次指示试验的选择(行,列,九宫格)。
不管如何,这个控制面板也引入了知识(信息),这个也是需要剔除的。
那就需要一个可信任的初始设置仪式(trusted setup ceremony),形象说,玩数独的人把机器放到一个黑房里,每个人蒙上眼保证随机性,带一个锡纸帽子用来屏蔽电波信号防止读心术(side-channel attack)。然后搞乱控制面板的顺序后,焊死。
- 最后要升级机器。
虽然不知道控制面板的顺序,但可以不断通过尝试去试错获得信息,这样就破坏了零知识,所以要升级。
直接用一台扫描仪把那一次卡片的组合全部扫描下来,然后一次性同时验证所有的实验序列,想通过试错来获得信息的方式直接堵死了。
zk-SNARKs在ZCash中的构造
为了在Zcash中拥有零知识隐私,根据网络共识规则确定交易有效性的函数必须返回交易是否有效的答案,而不披露它执行计算的任何信息。这是通过将网络的共识规则编码在zk-SNARKs内来实现的。在较高的层次上,zk-SNARKs 的工作方式是首先把你想要证明的东西转化成一个等价的形式,即知道一些代数方程的解。在下一节中,我们将简要概述如何将确定有效事务的规则转换为可以在候选解决方案中进行评估的公式,而不会向验证这些方程的各方透露任何敏感信息。
Computation → Arithmetic Circuit → R1CS → QAP → zk-SNARK
将交易有效性函数转换为数学表达式的第一步是将逻辑步骤分解为最小的可能操作,从而创建一个“算术电路”。类似于一个布尔电路,一个程序被编译成离散的,单个的步骤,比如,AND, OR, NOT,当一个程序被转换成一个算术电路时,它被分解成由加法、减法、乘法和除法等基本算术运算组成的单个步骤(尽管在我们的特定情况下,我们将避免使用除法)。
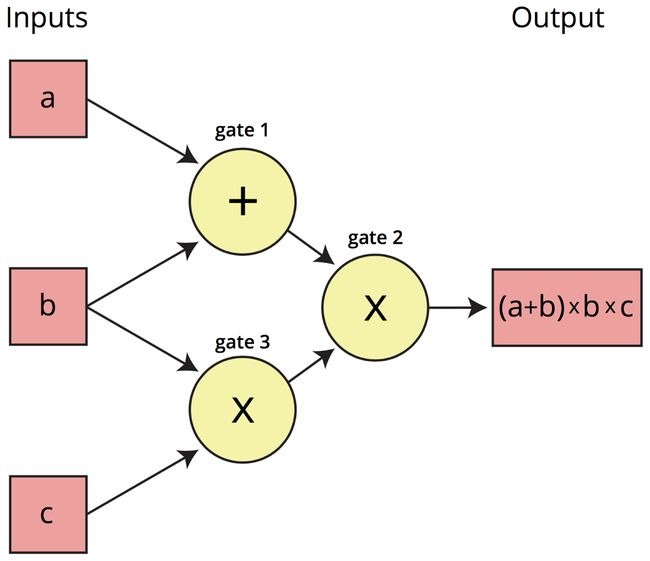
下面是计算表达式(a+b)(bc)的算术电路的示例:
观察这样的电路,我们可以把输入值a、b、c想象成在导线上从左到右向输出导线移动。我们的下一步是构建所谓的Rank 1约束系统(or R1CS),以检查值是否“正常运行”。在本例中,R1CS将确认,例如,来自b和c所在的乘法门的值是b*c。
在这个R1CS表示中,验证器必须检查许多约束——几乎对电路的每根导线都有一个约束。(由于技术上的原因,原来我们对来自乘法门的电线只有一个限制。)在2012年的一篇关于这一话题的论文中,Gennaro、Gentry、Parno和Raykova提出了一种很好的方式来“将所有这些约束捆绑在一起”。这种方法使用二次算术程序(QAP)表示电路。现在需要检查的唯一约束是多项式之间的约束,而不是数字之间的约束。多项式可以很大,但这是可以的,因为当一个恒等式在多项式之间不成立时,它在大多数点都不能成立。因此,你只需要检查两个多项式在一个随机选择的点上是否匹配,就可以正确验证高概率的证明。
如果验证者预先知道了哪个点,验证者会选择检查,他们可能能够处理无效的多项式,但是在那个点仍然满足身份。使用zk-SNARKs,可以使用复杂的数学技术,如同态加密和椭圆曲线的配对来“盲目”地评估多项式——即不知道要计算哪个点。上面描述的公共参数用于确定要检查哪个点,但是是以加密的形式,这样验证者和验证者都不知道它是什么。
到目前为止的描述主要讨论了如何在“SNARKs”中获取S和N——如何获得一个简短的、非交互的、单一的消息证明——但没有讨论“zk”(零知识)部分,该部分允许验证者保持其秘密输入的机密性。结果表明,在这一阶段,“zk”部分可以通过使验证者使用仍然满足所需标识的原始多项式的“随机移位”来轻松添加。