中值双边滤波

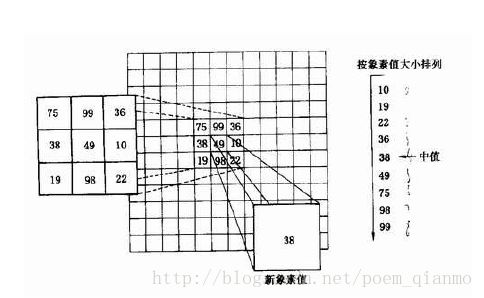
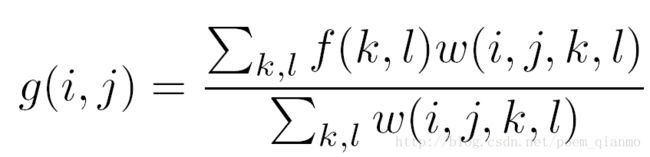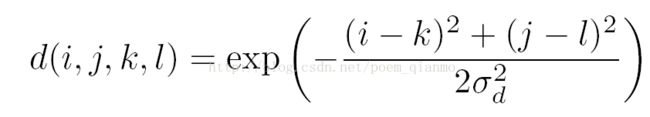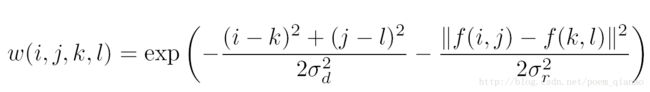中值滤波原理通过一张图就可以看明白：

简言之中值滤波就是把函数框（如图中的3 X 3）内的灰度值按顺序排列，然后中值取代函数框中心的灰度值。所以一般采用奇数点的邻域来计算中值，但如果像素点数为偶数，中值就取排序像素中间两点的平均值。

中值滤波在一定的条件下可以克服常见线性滤波器如方框滤波器、均值滤波等带来的图像细节模糊，而且对滤除脉冲干扰及图像扫描噪声非常有效，也常用于保护边缘信息, 保存边缘的特性使它在不希望出现边缘模糊的场合也很有用，是非常经典的平滑噪声处理方法。

但是中值滤波的缺点也很明显，因为要进行排序操作，所以处理的时间长，是均值滤波的5倍以上。

中值滤波在OpenCV中用medianBlur函数实现，下面是函数声明：

voidmedianBlur(InputArray src,OutputArray dst,intksize);

参数很简单，就是输入图像src，输出图像dst，以及核的大小ksize。注意这里的ksize必须为正奇数1,3,5,7……否则程序会出错。

三、双边滤波

双边滤波（Bilateral filter）是一种非线性的滤波方法，是结合图像的空间邻近度和像素值相似度的一种折衷处理，同时考虑空域信息和灰度相似性，达到保边去噪的目的。具有简单、非迭代、局部的特点。

双边滤波器的好处是可以做边缘保存（edge preserving），一般用高斯滤波去降噪，会较明显地模糊边缘，对于高频细节的保护效果并不明显。双边滤波器顾名思义比高斯滤波多了一个高斯方差sigma－d，它是基于空间分布的高斯滤波函数，所以在边缘附近，离的较远的像素不会太多影响到边缘上的像素值，这样就保证了边缘附近像素值的保存。但是由于保存了过多的高频信息，对于彩色图像里的高频噪声，双边滤波器不能够干净的滤掉，只能够对于低频信息进行较好的滤波。

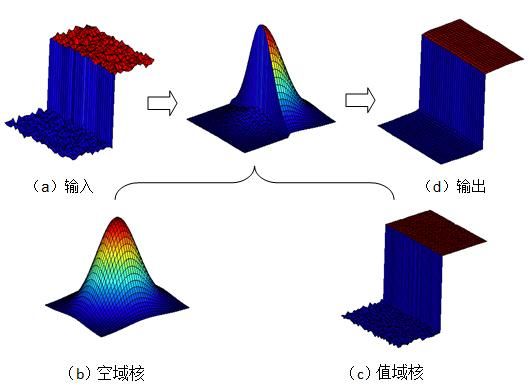
下图是双边滤波的原理示意图：

在双边滤波器中，输出像素的值依赖于邻域像素值的加权值组合：

而加权系数w(i,j,k,l)取决于空域核和值域核的乘积。

(i,j)，(k,l)分别指两个像素点的坐标。

其中空域核表示如下（如图）：

值域核表示为：

两者相乘后，就会产生依赖于数据的双边滤波权重函数：

d函数是根据像素距离选择权重，距离越近权重越大，这一点和方框滤波，高斯滤波方式相同。而r函数则是根据像素的差异来分配权值。如果两个像素值越接近，即使相距较远，也比差异大而距离近的像素点权重大。正是r函数的作用，使得边缘，即相距近但差异大的像素点的特性得以保留。

OpenCV中用medianBlur函数实现双边滤波。

函数声明：

voidbilateralFilter(InputArray src,OutputArray dst,intd,doublesigmaColor,doublesigmaSpace,intborderType=BORDER_DEFAULT);

参数：

第一个参数，InputArray类型的src，输入图像，即源图像，需要为8位或者浮点型单通道、三通道的图像。

第二个参数，OutputArray类型的dst，即目标图像，需要和源图片有一样的尺寸和类型。

第三个参数，int类型的d，表示在过滤过程中每个像素邻域的直径。如果这个值我们设其为非正数，那么OpenCV会从第五个参数sigmaSpace来计算出它来。

第四个参数，double类型的sigmaColor，颜色空间滤波器的sigma值。这个参数的值越大，就表明该像素邻域内有更宽广的颜色会被混合到一起，产生较大的半相等颜色区域。

第五个参数，double类型的sigmaSpace坐标空间中滤波器的sigma值，坐标空间的标注方差。他的数值越大，意味着越远的像素会相互影响，从而使更大的区域足够相似的颜色获取相同的颜色。当d>0，d指定了邻域大小且与sigmaSpace无关。否则，d正比于sigmaSpace。

第六个参数，int类型的borderType，用于推断图像外部像素的某种边界模式。注意它有默认值BORDER_DEFAULT。

四、示例代码：

#include"opencv2/core/core.hpp  

"#include"opencv2/highgui/highgui.hpp

 "#include 

#include 

using namespace cv;                                                       

intmain()

{

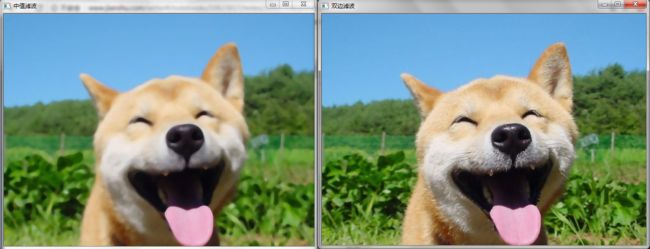
Mat img=imread("dog.jpg");//据说丑女经过双边滤波用有美颜效果哦，有兴趣的同学可以试试                             

 Mat out1,out2,out3;

medianBlur(img,out1,35);

bilateralFilter(img,out2,25,25*2,25/2);

namedWindow("中值滤波",2);

imshow("中值滤波",out1);

namedWindow("双边滤波",2);

imshow("双边滤波",out2);

waitKey(0);

return0;

}

双边滤波算法原理

双边滤波是一种非线性滤波器，它可以达到保持边缘、降噪平滑的效果。和其他滤波原理一样，双边滤波也是采用加权平均的方法，用周边像素亮度值的加权平均代表某个像素的强度，所用的加权平均基于高斯分布[1]。最重要的是，双边滤波的权重不仅考虑了像素的欧氏距离（如普通的高斯低通滤波，只考虑了位置对中心像素的影响），还考虑了像素范围域中的辐射差异（例如卷积核中像素与中心像素之间相似程度、颜色强度，深度距离等），在计算中心像素的时候同时考虑这两个权重。 公式1a,1b给出了双边滤过的操作，Iq为输入图像，Ipbf为滤波后图像：

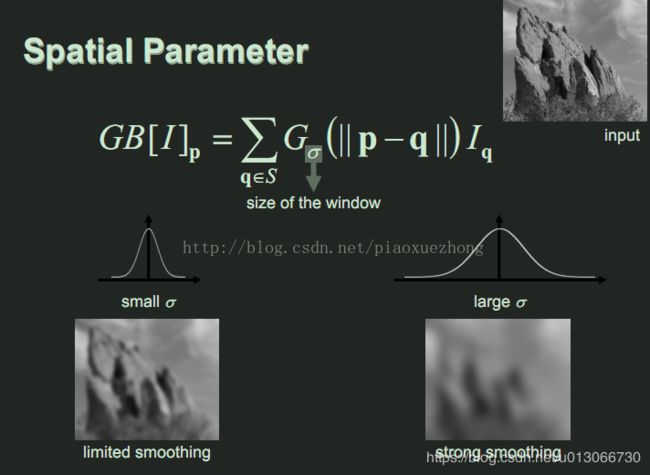
mark下双边滤波里的两个权重域的概念：空间域（spatial domain S）和像素范围域（range domain R）,这个是它跟高斯滤波等方法的最大不同点。下面是我找到的对比说明，更好地理解双边滤波，首先是高斯滤波的情况：

然后对比再看一下双边滤波的过程：

双边滤波的核函数是空间域核与像素范围域核的综合结果：在图像的平坦区域，像素值变化很小，对应的像素范围域权重接近于1，此时空间域权重起主要作用，相当于进行高斯模糊；在图像的边缘区域，像素值变化很大，像素范围域权重变大，从而保持了边缘的信息。

为了更加形象的说明两个权重的影响，作者还给出了二维图像的直观说明:

双边滤波算法实现

在原理部分，从双边滤波的公式就可以得到该算法的实现途径。由于直接的编码实现上述过程，其时间复杂度为O(σs2) ，比较耗时，所以后来出现了一些改进算法，比较经典的有：论文《Fast O(1) bilateral filtering using trigonometric range kernels》，提出了用Raised cosines函数来逼近高斯值域函数，并利用一些特性把值域函数分解为一些列函数的叠加，从而实现函数的加速[5，8]。

这里只对原始方法进行实现，从而有助于更加清楚的了解算法的原理。

matlab实现方法，这里也附一下核心代码：

functionoutput = bilateralFilter( data, edge, sigmaSpatial, sigmaRange, ...

    samplingSpatial, samplingRange )

if~exist('edge', 'var' ),

    edge = data;

end

inputHeight = size( data,1);

inputWidth = size( data,2);

if~exist('sigmaSpatial', 'var' ),

sigmaSpatial = min( inputWidth, inputHeight ) /16;

end

edgeMin = min( edge( : ) );

edgeMax = max( edge( : ) );

edgeDelta = edgeMax - edgeMin;

if~exist('sigmaRange', 'var' ),

sigmaRange =0.1* edgeDelta;

end

if~exist('samplingSpatial', 'var' ),

    samplingSpatial = sigmaSpatial;

end

if~exist('samplingRange', 'var' ),

    samplingRange = sigmaRange;

end

ifsize( data ) ~= size( edge ),

error('data and edge must be of the same size' );

end

% parameters

derivedSigmaSpatial = sigmaSpatial / samplingSpatial;

derivedSigmaRange = sigmaRange / samplingRange;

paddingXY = floor(2* derivedSigmaSpatial ) +1;

paddingZ = floor(2* derivedSigmaRange ) +1;

% allocate3D grid

downsampledWidth = floor( ( inputWidth -1) / samplingSpatial ) +1+2* paddingXY;

downsampledHeight = floor( ( inputHeight -1) / samplingSpatial ) +1+2* paddingXY;

downsampledDepth = floor( edgeDelta / samplingRange ) +1+2* paddingZ;

gridData = zeros( downsampledHeight, downsampledWidth, downsampledDepth );

gridWeights = zeros( downsampledHeight, downsampledWidth, downsampledDepth );

% compute downsampled indices

[ jj, ii ] = meshgrid(0: inputWidth -1,0: inputHeight -1);

di = round( ii / samplingSpatial ) + paddingXY +1;

dj = round( jj / samplingSpatial ) + paddingXY +1;

dz = round( ( edge - edgeMin ) / samplingRange ) + paddingZ +1;

% perform scatter (there's probably a faster way than this)

% normally woulddodownsampledWeights( di, dj, dk ) =1, but we haveto

% perform a summationtodobox downsampling

fork =1: numel( dz ),

dataZ = data( k ); % traverses the image column wise, sameasdi( k )

if~isnan( dataZ  ),

        dik = di( k );

        djk = dj( k );

        dzk = dz( k );

        gridData( dik, djk, dzk ) = gridData( dik, djk, dzk ) + dataZ;

gridWeights( dik, djk, dzk ) = gridWeights( dik, djk, dzk ) +1;

end

end

% make gaussian kernel

kernelWidth =2* derivedSigmaSpatial +1;

kernelHeight = kernelWidth;

kernelDepth =2* derivedSigmaRange +1;

halfKernelWidth = floor( kernelWidth /2);

halfKernelHeight = floor( kernelHeight /2);

halfKernelDepth = floor( kernelDepth /2);

[gridX, gridY, gridZ] = meshgrid(0: kernelWidth -1,0: kernelHeight -1,0: kernelDepth -1);

gridX = gridX - halfKernelWidth;

gridY = gridY - halfKernelHeight;

gridZ = gridZ - halfKernelDepth;

gridRSquared = ( gridX .* gridX + gridY .* gridY ) / ( derivedSigmaSpatial * derivedSigmaSpatial ) + ( gridZ .* gridZ ) / ( derivedSigmaRange * derivedSigmaRange );

kernel = exp(-0.5* gridRSquared );

% convolve

blurredGridData = convn( gridData, kernel,'same' );

blurredGridWeights = convn( gridWeights, kernel,'same' );

% divide

blurredGridWeights( blurredGridWeights ==0) =-2; % avoid divideby0, won't read there anyway

normalizedBlurredGrid = blurredGridData ./ blurredGridWeights;

normalizedBlurredGrid( blurredGridWeights <-1) =0; % put0swhereit's undefined

blurredGridWeights( blurredGridWeights <-1) =0; % put zeros back

% upsample

[ jj, ii ] = meshgrid(0: inputWidth -1,0: inputHeight -1); % meshgrid does x,theny, so output arguments needtobe reversed

% no rounding

di = ( ii / samplingSpatial ) + paddingXY +1;

dj = ( jj / samplingSpatial ) + paddingXY +1;

dz = ( edge - edgeMin ) / samplingRange + paddingZ +1;

% interpn takes rows,thencols, etc

% i.e. size(v,1),thensize(v,2), ...

output = interpn( normalizedBlurredGrid, di, dj, dz );

 双边滤波算法实例：

%% 测试函数，其中参数设置请参见函数注释

clc,clear all,close all;

ori=imread('D:\proMatlab\vessel_edge_extration\image\3.jpg');

ori=double(rgb2gray(ori))/255.0;

[width, height]=size(ori);

sigmaSpatial  = min( width, height ) /30;

samplingSpatial=sigmaSpatial;

sigmaRange = ( max( ori( : ) ) - min( ori( : ) ) ) /30;

samplingRange= sigmaRange;

output = bilateralFilter( ori, ori, sigmaSpatial, sigmaRange, ...

    samplingSpatial, samplingRange );

figure,

subplot(1,2,1),imshow(ori,[]);title('input image');

subplot(1,2,2),imshow(output,[]);title('output image');

论文参考：

https://jianshu.com/p/8d11e26c9665

https://blog.csdn.net/u013066730/article/details/87859184