开始

本文使用
■Python2.7
■numpy 1.11
■scipy 0.17
■scikit-learn 0.18
■matplotlib 1.5
■seaborn 0.7
■pandas 0.17。

本文所用代码都在jupyter notebook上确认没有问题。（用jupyter notebook的时候请指定%matplotlib inline）。
本文参考了scikit-learn的《流形学习》的内容。

我们用scikit-learn的手写数字识别示例来说明所谓流形学习的方法。特别是可以用来做高维数据可视化的方法，比如t-SNE方法在Kaggle竞赛中有时就会用到。但是这些方法并不是只用在可视化方面，当这些方法结合了原始数据和压缩后的数据，可以提高单纯的分类问题的精度。

from time import time

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import offsetbox
from sklearn import (manifold, datasets, decomposition, ensemble,
                     discriminant_analysis, random_projection)

digits = datasets.load_digits(n_class=6)
X = digits.data
y = digits.target
n_samples, n_features = X.shape
n_neighbors = 30

n_img_per_row = 20
img = np.zeros((10 * n_img_per_row, 10 * n_img_per_row))
for i in range(n_img_per_row):
    ix = 10 * i + 1
    for j in range(n_img_per_row):
        iy = 10 * j + 1
        img[ix:ix + 8, iy:iy + 8] = X[i * n_img_per_row + j].reshape((8, 8))

plt.imshow(img, cmap=plt.cm.binary)
plt.xticks([])
plt.yticks([])
plt.title('A selection from the 64-dimensional digits dataset')

image.png

准备Digit数据映射用的函数。
下面的代码跟文章的主题关系不大，如果理解起来困难的话，可以跳过。

def plot_embedding(X, title=None):
    x_min, x_max = np.min(X, 0), np.max(X, 0)
    X = (X - x_min) / (x_max - x_min)

    plt.figure()
    ax = plt.subplot(111)
    for i in range(X.shape[0]):
        plt.text(X[i, 0], X[i, 1], str(digits.target[i]),
                 color=plt.cm.Set1(y[i] / 10.),
                 fontdict={'weight': 'bold', 'size': 9})

    if hasattr(offsetbox, 'AnnotationBbox'):
        # only print thumbnails with matplotlib > 1.0
        shown_images = np.array([[1., 1.]])  # just something big
        for i in range(digits.data.shape[0]):
            dist = np.sum((X[i] - shown_images) ** 2, 1)
            if np.min(dist) < 4e-3:
                # don't show points that are too close
                continue
            shown_images = np.r_[shown_images, [X[i]]]
            imagebox = offsetbox.AnnotationBbox(
                offsetbox.OffsetImage(digits.images[i], cmap=plt.cm.gray_r),
                X[i])
            ax.add_artist(imagebox)
    plt.xticks([]), plt.yticks([])
    if title is not None:
        plt.title(title)

2. 着眼于线性成分的降维

这里介绍的方法，因为计算成本较低，通用性高，经常要用到。
例如，用PCA算法抽出数据之间的相关性非常方便。这里的方法很多资料有详细的说明，本文中就不在展开介绍了。

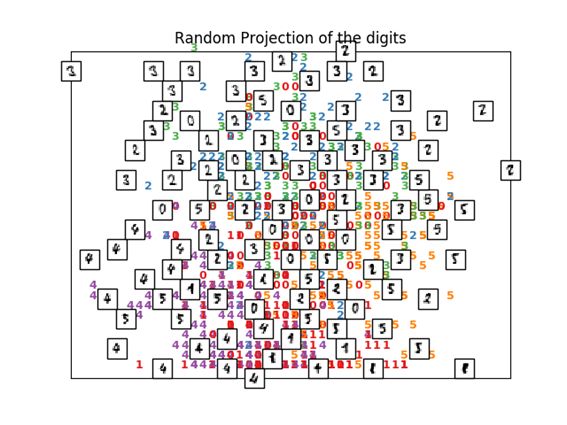
2.1. Random Projection
在第1节中已经取得64维的手写数字数据。
这样高维数据进行映射的最基本方法是Random Projection，中文叫随机投影。
非常简单的方法，用随机数来设定将M维的数据映射到N维的矩阵R中的元素。这样做的好处是计算量非常小。

print("Computing random projection")
rp = random_projection.SparseRandomProjection(n_components=2, random_state=42)
X_projected = rp.fit_transform(X)
plot_embedding(X_projected, "Random Projection of the digits")
#plt.scatter(X_projected[:, 0], X_projected[:, 1])

image.png

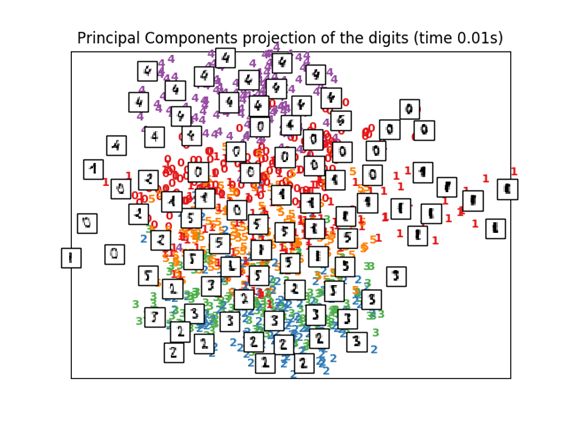
2.2. PCA
用PCA映射，是一般的维度压缩方法。可以抽出变量间的相关成分。
这里我们使用scikit-learn中提供的函数TruncatedSVD。这个函数跟PCA不同的地方好像只是输入数据是否经过正规化。

print("Computing PCA projection")
t0 = time()
X_pca = decomposition.TruncatedSVD(n_components=2).fit_transform(X)
plot_embedding(X_pca,
               "Principal Components projection of the digits (time %.2fs)" %(time() - t0))

image.png

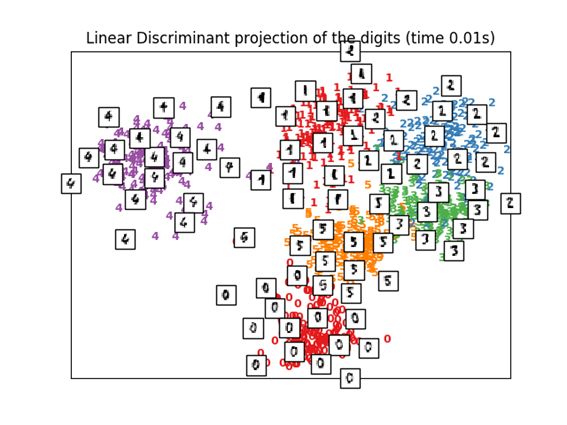
2.3 Linear Discriminant Analysis
可以通过Linear Discriminant Analysis（线性判别分析）来进行降维。前提是各个变量都服从多元正态分布，同一组变量具有相同的协方差矩阵。使用的距离是马氏距离（Mahalanobis distance）。
跟PCA相似，这个算法也属于监督学习。

print("Computing Linear Discriminant Analysis projection")
X2 = X.copy()
X2.flat[::X.shape[1] + 1] += 0.01  # Make X invertible
t0 = time()
X_lda = discriminant_analysis.LinearDiscriminantAnalysis(n_components=2).fit_transform(X2, y)
plot_embedding(X_lda,
               "Linear Discriminant projection of the digits (time %.2fs)" %
               (time() - t0))

image.png

3. 考虑非线性成分的降维

刚刚介绍的3种方法，对于具有层级构造的数据和含有非线性成分的数据进行降维是不适用的。比如这里介绍一下像swiss roll一样的线性无关数据的2维图像。

image.png

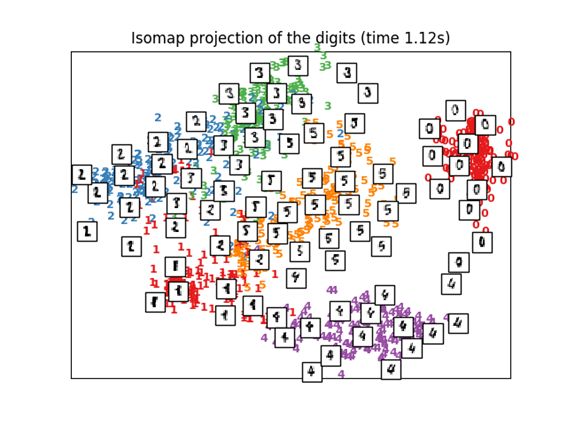
3.1 Isomap
Isomap是考虑非线性数据进行降维和聚类的方法之一。
沿着流形的形状计算叫做测地距离的距离，根据这个距离来进行多尺度缩放。
这里可以用Scikit-learn的Isomap函数。计算距离的阶段，可以使用BallTree函数。

print("Computing Isomap embedding")
t0 = time()
X_iso = manifold.Isomap(n_neighbors, n_components=2).fit_transform(X)
print("Done.")
plot_embedding(X_iso,
               "Isomap projection of the digits (time %.2fs)" %
               (time() - t0))

image.png

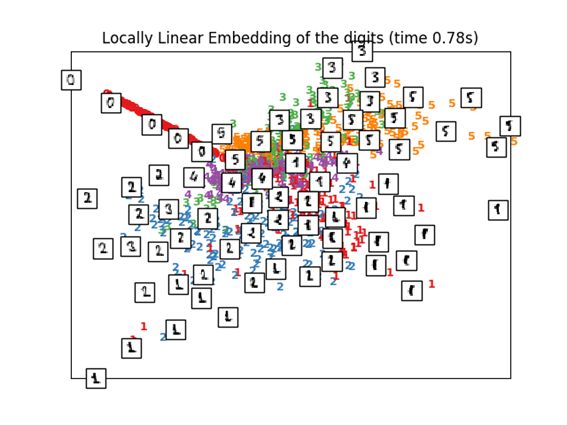
3.2 Locally Linear Embedding（LLE）
即使从全局来看，包含非线性的流形，从局部着眼来看的话也有基于直觉的线性降维方法。下面的例子中，可以看到标签0被突出的显示出来，其他的标签还是混乱的。

print("Computing LLE embedding")
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2,
                                      method='standard')
t0 = time()
X_lle = clf.fit_transform(X)
print("Done. Reconstruction error: %g" % clf.reconstruction_error_)
plot_embedding(X_lle,
               "Locally Linear Embedding of the digits (time %.2fs)" %
               (time() - t0))

image.png

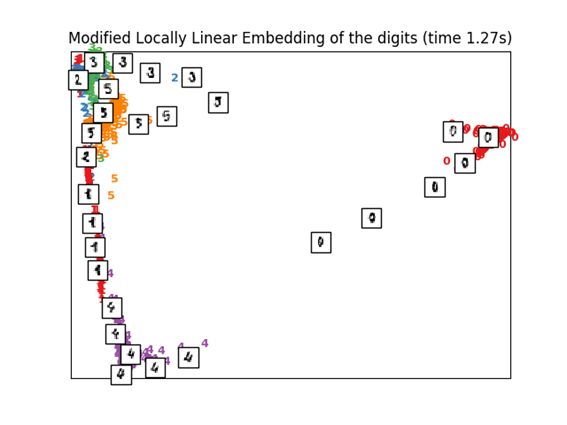
3.3. Modified Locally Linear Embedding
LLE本身存在问题，所以就有了用正规化来来改良的算法。
从改良的算法结果可以看出标签0被清楚地分类，标签4,1,5也被清晰地映射出来。

print("Computing modified LLE embedding")
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2,
                                      method='modified')
t0 = time()
X_mlle = clf.fit_transform(X)
print("Done. Reconstruction error: %g" % clf.reconstruction_error_)
plot_embedding(X_mlle,
               "Modified Locally Linear Embedding of the digits (time %.2fs)" %
               (time() - t0))

image.png

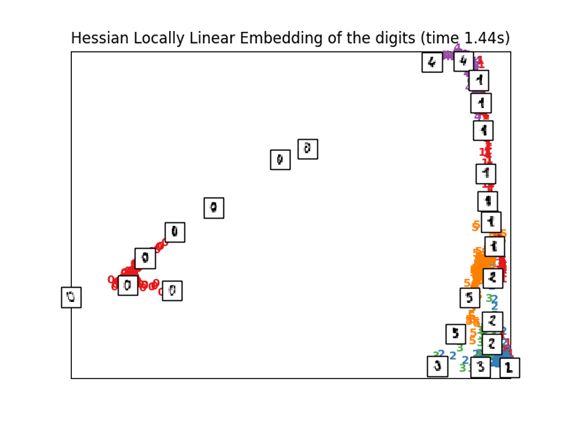
3.4 Hessian LLE Embedding
LLE本身存在问题，所以就有了用正规化来来改良的算法。
这个是第二个修改方案。

print("Computing Hessian LLE embedding")
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2,
                                      method='hessian')
t0 = time()
X_hlle = clf.fit_transform(X)
print("Done. Reconstruction error: %g" % clf.reconstruction_error_)
plot_embedding(X_hlle,
               "Hessian Locally Linear Embedding of the digits (time %.2fs)" %
               (time() - t0))

image.png

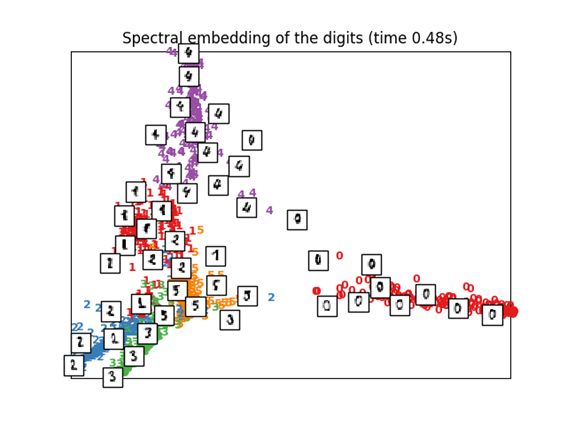
3.5 Spectral Embedding
这是也可以称为拉普拉斯特征映射（Laplacian Eigenmaps）的一种压缩方法。
这里没有对专门的内容进行调查，好像其中使用了光谱图理论。
映射的形式与LLE，MLLE，HLLE都不同，标签组之间的距离以及密集度似乎表现上类似。

print("Computing Spectral embedding")
embedder = manifold.SpectralEmbedding(n_components=2, random_state=0,
                                      eigen_solver="arpack")
t0 = time()
X_se = embedder.fit_transform(X)

plot_embedding(X_se,
               "Spectral embedding of the digits (time %.2fs)" %
               (time() - t0))

image.png

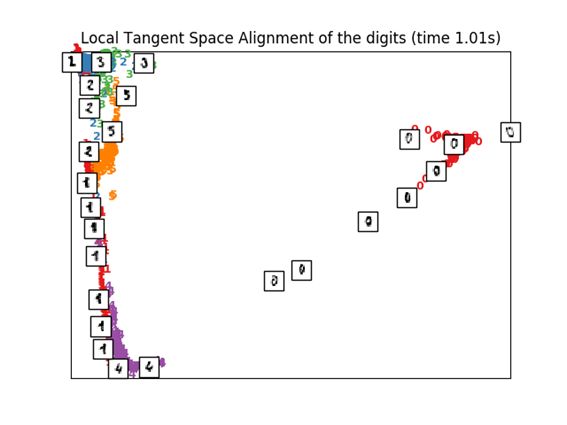
3.6 Local Tangent Space Alignment
这个算法的结果很像MLLE，HLLE的反转。分类结果很相似的感觉。

print("Computing LTSA embedding")
clf = manifold.LocallyLinearEmbedding(n_neighbors, n_components=2,
                                      method='ltsa')
t0 = time()
X_ltsa = clf.fit_transform(X)
print("Done. Reconstruction error: %g" % clf.reconstruction_error_)
plot_embedding(X_ltsa,
               "Local Tangent Space Alignment of the digits (time %.2fs)" %
               (time() - t0))

image.png

3.7 Multi-dimensional Scaling (MDS)
这是一种叫做多维缩放分析的降维方法。
MDS本身是多种方法的总称，这里不做详细说明。

print("Computing MDS embedding")
clf = manifold.MDS(n_components=2, n_init=1, max_iter=100)
t0 = time()
X_mds = clf.fit_transform(X)
print("Done. Stress: %f" % clf.stress_)
plot_embedding(X_mds,
               "MDS embedding of the digits (time %.2fs)" %
               (time() - t0))

image.png

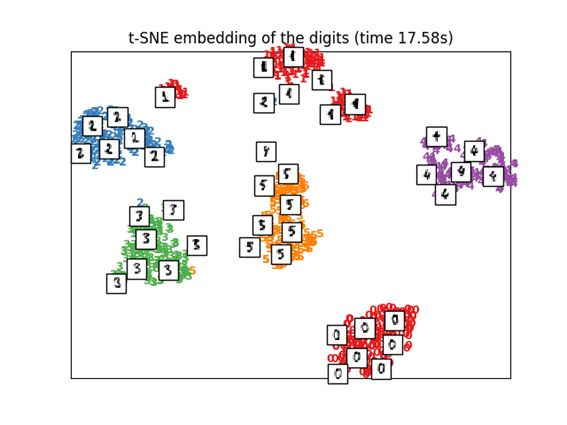
3.8 t-distributed Stochastic Neighbor Embedding (t-SNE)
将各个点之间的欧几里得距离变换成条件概率而不是相似度，并将其映射到低维。
有一种叫Barnes-Hut t-SNE的方法，牺牲精度换取降低计算成本。在Sklearn中，可以选择exact（重视精度）和Barnes-Hut两种选择。默认是选择Barnes-Hut方法。可以通过设定参数angle选项的值来调参。
Kaggle比赛中频繁使用的一种方法。

print("Computing t-SNE embedding")
tsne = manifold.TSNE(n_components=2, init='pca', random_state=0)
t0 = time()
X_tsne = tsne.fit_transform(X)

plot_embedding(X_tsne,
               "t-SNE embedding of the digits (time %.2fs)" %
               (time() - t0))

image.png

3.9 Random Forest Embedding

print("Computing Totally Random Trees embedding")
hasher = ensemble.RandomTreesEmbedding(n_estimators=200, random_state=0,
                                       max_depth=5)
t0 = time()
X_transformed = hasher.fit_transform(X)
pca = decomposition.TruncatedSVD(n_components=2)
X_reduced = pca.fit_transform(X_transformed)

plot_embedding(X_reduced,
               "Random forest embedding of the digits (time %.2fs)" %
               (time() - t0))

image.png

高维数据的降维和2维可视化方法

开始

目录

1. 生成数据

2. 关注线性属性的降维

3. 考虑非线性成分的降维

1. 生成数据

2. 着眼于线性成分的降维

3. 考虑非线性成分的降维

你可能感兴趣的:(高维数据的降维和2维可视化方法)