散列表(Hash table,也叫哈希表)是一种通过将键(key)映射为值(value)从而实现快速查找的数据结构。
- 若关键字为 k,则其值存放在f(k)的存储位置上。由此,不需比较便可直接取得所查记录。称这个对应关系 f 为散列函数,按这个思想建立的表为散列表。
- 对不同的关键字k可能得到同一散列地址,即k1!=k2,而f(k1)=f(k2),这种现象称为冲突(或碰撞,英语:Collision)。具有相同函数值的关键字对该散列函数来说称做同义词。综上所述,根据散列函数f(k)和处理冲突的方法将一组关键字映射到一个有限的连续的地址集(区间)上,并以关键字在地址集中的“像”作为记录在表中的存储位置,这种表便称为散列表,这一映射过程称为散列造表或散列,所得的存储位置称散列地址。
- 若对于关键字集合中的任一个关键字,经散列函数映象到地址集合中任何一个地址的概率是相等的,则称此类散列函数为均匀散列函数(Uniform Hash function),这就使关键字经过散列函数得到一个“随机的地址”,从而减少冲突。
-
聚集(Cluster,也翻译做“堆积”)的意思是,在函数地址的表中,散列函数的结果不均匀地占据表的单元,形成区块,造成线性探测产生一次聚集(primary clustering)和平方探测的二次聚集(secondary clustering),散列到区块中的任何关键字需要查找多次试选单元才能插入表中,解决冲突,造成时间浪费。对于开放定址法,聚集会造成性能的灾难性损失,是必须避免的
处理冲突
1)开放寻址(Open Addressing)法:
所有的元素都在散列表中,每一个表项或包含动态集合的一个元素,或包含NIL。这种方法中散列表可能被填满,以致于不能插入任何新的元素。在开放寻址法中,当要插入一个元素时,可以连续地检查或探测散列表的各项,直到有一个空槽来放置待插入的关键字为止。
有三种技术用于开放寻址法:线性探测、二次探测以及双重探测。
<1>线性探测
给定一个普通的散列函数h':U —>{0,1,.....,m-1},线性探测方法采用的散列函数为:h(k,i) = (h'(k)+i)mod m,i=0,1,....,m-1
探测时从i=0开始,首先探查T[h'(k)],然后依次探测T[h'(k)+1],…,直到T[h'(k)+m-1],此后又循环到T[0],T[1],…,直到探测到T[h'(k)-1]为止。探测过程终止于三种情况:
(1)若当前探测的单元为空,则表示查找失败(若是插入则将key写入其中);
(2)若当前探测的单元中含有key,则查找成功,但对于插入意味着失败;
(3)若探测到T[h'(k)-1]时仍未发现空单元也未找到key,则无论是查找还是插入均意味着失败(此时表满)。
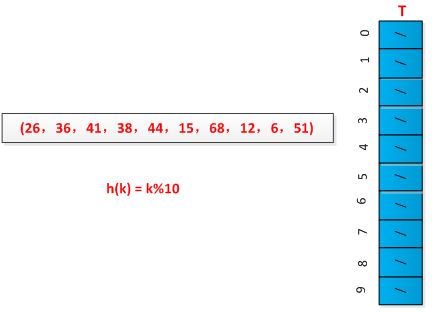
线性探测方法较容易实现,但是存在一次群集问题,即连续被占用的槽的序列变的越来越长。采用例子进行说明线性探测过程,已知一组关键字为(26,36,41,38,44,15,68,12,6,51),用除余法构造散列函数,初始情况如下图所示:
<2>二次探测
二次探测法的探查序列是:h(k,i) =(h'(k)+i*i)%m ,0≤i≤m-1 。初次的探测位置为T[h'(k)],后序的探测位置在次基础上加一个偏移量,该偏移量以二次的方式依赖于i。该方法的缺陷是不易探查到整个散列空间。
<3>双重散列
该方法是开放寻址的最好方法之一,因为其产生的排列具有随机选择的排列的许多特性。采用的散列函数为:h(k,i)=(h1(k)+ih2(k)) mod m。其中h1和h2为辅助散列函数。初始探测位置为T[h1(k)],后续的探测位置在此基础上加上偏移量h2(k)模m。
2)链接(Chaining)法:
将所有关键字为同义词的结点链接在同一个链表中。若选定的散列表长度为m,则可将散列表定义为一个由m个头指针组成的指针数组T[0..m-1]。凡是散列地址为i的结点,均插入到以T[i]为头指针的单链表中。T中各分量的初值均应为空指针。在拉链法中,装填因子α可以大于1,但一般均取α≤1。
举例说明链接法的执行过程,设有一组关键字为(26,36,41,38,44,15,68,12,6,51),用除余法构造散列函数,初始情况如下图所示:
最终结果如下图所示:
3)除了在链表中存储冲突元素,还可以将冲突元素存储在二叉搜索树中。
这会使得最坏情况下的运行时间达到O(logN)。实际上,除非出现非常不均匀的分布,否则很少采用这种方法。
时间复杂度
如果冲突发生很多次,最坏的情况下的时间复杂度是O(N) ,其中N是键的数量。
但是我们通常假设一个不错的实现方式会将冲突数量保持在最低水平,在此情况下,时间复杂度是O(1)
另一种方法是通过平衡二叉搜索树实现散列表。该方法的查找时间是O(logN)。该方法的好处是用到的空间可能更少,因为我们不再需要分配一个大数组,还可以按照键的顺序进行迭代访问。
构造散列函数的方法
散列函数能使对一个数据序列的访问过程更加迅速有效,通过散列函数,数据元素将被更快定位。
- 直接定址法:取关键字或关键字的某个线性函数值为散列地址。即hash(k)=k 或hash(k)=ak+b, 其中ab为常数(这种散列函数叫做自身函数)
- 数字分析法:假设关键字是以r为基的数,并且哈希表中可能出现的关键字都是事先知道的,则可取关键字的若干数位组成哈希地址。
- 平方取中法:取关键字平方后的中间几位为哈希地址。通常在选定哈希函数时不一定能知道关键字的全部情况,取其中的哪几位也不一定合适,而一个数平方后的中间几位数和数的每一位都相关,由此使随机分布的关键字得到的哈希地址也是随机的。取的位数由表长决定。
- 折叠法:将关键字分割成位数相同的几部分(最后一部分的位数可以不同),然后取这几部分的叠加和(舍去进位)作为哈希地址。
- 除留余数法:取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即 hash(k)=k mod p, p<=m。不仅可以对关键字直接取模,也可在折叠法、平方取中法等运算之后取模。对p的选择很重要,一般取素数或m,若p选择不好,容易产生冲突。
拉宾-卡普(Rabin-Karp)子串查找