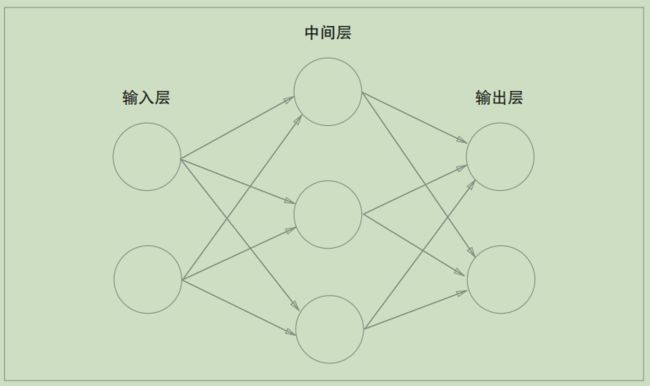
神经网络的图解
感知机,是人工设置权重。让它的输出值符合预期。
而神经网络的一个重要性质是它可以自动地从数据中学习到合适的权重参数。
如果用图来表示神经网络,最左边的一列称为输入层,最右边的一列称为输出层,中间的一列称为中间层。中间层有时也称为隐藏层.如下图:
之前,文章中:https://www.cnblogs.com/zhangshengdong/p/12613674.html 提到了激活函数(activation function),用于激活神经元。
一般的激活函数有,sigmoid函数,ReLU函数等。
sigmoid函数
sigmoid函数的公式:
\[h(x)=\frac{1}{(1+\mathrm{e}^{-x})} \]
比如,向sigmoid函数输入1.0或2.0后,就会有某个值被输出,类似h(1.0) = 0.731 ...、h(2.0) = 0.880 ...。是一个非线性函数。
代码如下:
import numpy as np
import matplotlib.pylab as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
X = np.arange(-5.0, 5.0, 0.1)
Y = sigmoid(X)
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)
plt.show()
图形如下:
如果考虑把线性函数 h(x) = cx 作为激活函数,把y(x) = h(h(h(x)))的运算对应3层神经网络。这个运算会进行y(x) = c * c * c * x的乘法运算,但是同样的处理可以由y(x) = ax(注意,\(a=c^3\))这一次乘法运算(即没有隐藏层的神经网络)来表示。如本例所示,使用线性函数时,无法发挥多层网络带来的优势。因此,为了发挥叠加层所带来的优势,激活函数必须使用非线性函数。
ReLU函数
ReLU函数的公式
\[h(x)= \begin{cases} x (x > 0)\\ 0 (x <= 0) \end{cases} \]
最近在神经网络中,也有很多场景下使用最近使用ReLU(Rectified Linear Unit)函数
代码如下:
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
def relu(x):
return np.maximum(0, x)
x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1.0, 5.5)
plt.show()