序
今天跟qs聊了会,她放出了我的小时的照片,毕竟黑历史谁都有
然后,Singercoder 极限卡篮,还有就是,我又掉 rating 了,我也想去 NOI 呀
PS: Singercoder 掉青 2020/3/7
update: 2020/3/23 相应 Singercoder 所做的笔记
个人认为 Singercoder 的笔记写的是真的清晰 ,但无奈码风过于毒瘤了
KMP
前言
KMP 算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt提出的,因此人们称它为克努特—莫里斯—普拉特操作(简称KMP算法)。
说句闲话
先说一下字符串匹配的定义,就是一个给你一个主串 S 一个模式串 T 然后求 T 在 S 里出现的每个位置
没有学KMP之前,我会两种字符串匹配算法,一个是朴素匹配,一个是有限自动机(不算是会,就是了解一下)但是这两个算法复杂度无疑可以卡成 \(O(nm)\), 是无法接受的,然而这闲的没事干的三人把字符串匹配做成了线性的 %%%。
但是似乎在 oi 里的用处不是很大吧,我从来也没在题里用过他,除了板子题
正文
来介绍一种 Knuth-Morris-Pratt 算法 这个算法可以做到在 \(O(n + m)\) 时间内完成模式串和主串的匹配,利用了前缀的一些性质,用到了辅助函数 \(\pi\)
看算法的请往跳过,这里说的是原理
关于模式的前缀函数
这个算法的核心思想就在于此了,一个 \(\pi\) 函数。它包含了模式与其自身的偏移的信息。这些信息在朴素匹配中没有利用到所以慢。
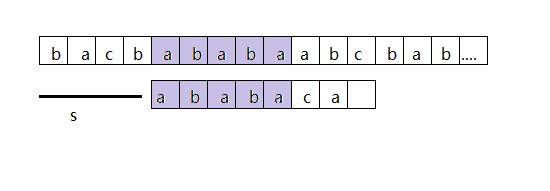
考察一下朴素字符串匹配的操作过程,下图正是朴素里一个匹配中的情景
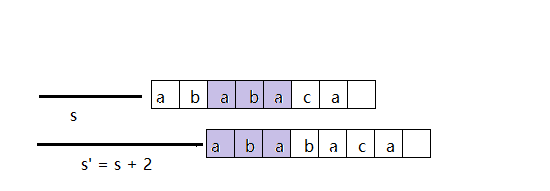
我们可以看到,\(q = 5\) 个字符已经匹配成功了,那么我们知道的这 \(q\) 个字符可以为我们知道一些不必要的偏移了。在这个实例中,显然偏移为 s + 1 是无用的,因为第一个字符 (a) 将于文本匹配,但是该模式串的第二个字符 (b) 并不能于匹配。如下图所示,偏移 s' = s + 2 使模式串的前三个字符与后三个字符匹配
前方高能!
我们知道下面问题的 answer 是很有用的:
假设模式串 \(T[1...q]\) 和主串 \(S[s + 1.. S+q]\) 匹配,\(s'\) 是最小的偏移量, \(s' > s\) , 那么对于某些 \(k < q\) ,满足
的最小偏移 \(s' > s\) 其中 \(s' + k = s + q\) 是什么?
话句话说,已知 \(T_q\sqsupset S_{s+q}\) (\(a\sqsupset b\) 表示 a 是 b 的后缀) 我们想要找到 \(T_q\) 的最长真前缀 k,也是 \(S_{s+q}\) 的后缀(找到 \(k\) 等价于写出了 \(s'\) ) 显然的有 $s'= s + q - k $ .于是我们可以预先处理出这些 \(k\) 用 \(\pi\) 数组存起来.
并且我们发现,求解这些信息就是一个 \(T\) 与其自身的匹配过程,下面来模拟一下过程以形象的说明.已知一个模式串 \(T[1..m]\) 前缀函数 \(\pi : \{1...m\}\rightarrow\{0...m - 1\}\) 满足
下图给出了一个完整的 \(\pi\) 函数
我们求解这个数组无疑就是自身与自身的匹配过程
代码实现
给出一种很巧妙的方法,我们不妨先设 pi[0] = -1 这可以减少码量
我们呢不妨假设 \(pi\) 已求出,现在要主串S与模式串T匹配
具体的时候,因为实现的问题,我们无需记录偏移量 \(s\) ,而是维护两个指针 \(i,j\).
for(i = 1; i <= lens; i++){
while(j > -1 && T[j+1] != S[i]) j = pi[j];
if(++j == lent) printf("%d\n", i - lenb + 1);
}
可以理解为如果下一个字符不匹配那么就要做偏移了.直到一样或者无法偏移了
$ \pi$ 就是 \(T\) 与其本身的每个后缀的最长公共前缀.我们求解 $ \pi$ 的过程就是 \(T\) 与其本身的的匹配(但是不要从第一个开始)
特别地我们有一条引理 \(\pi[i] \le \pi[i - 1] + 1\)
所以程序写的十分巧妙.
pi[0] = -1;
for(int i = 1; i <= lenb; i++){
int j = pi[i - 1];
while(j > -1 && T[i] != T[j+1]) j = pi[j];
pi[i]=j+1;
}
exKMP
PS:会补充的
exKMP 解决的是这么一个问题,给你主串 S 和 字串 T,问题对于 S 的每个后缀 ,与 T 的最长公共前缀的长度
我们先定义数组:
在这里,我们不妨设 z 已求出,我们的任务是求解 p
在下面的表述方法中,对于一个字符串 S,记 \(S_i\) 为 S 的第 i 个字符,\(S_{l \sim r}\) 为 S 从第 l 个字符起到第 r 个字符结束形成的子串
考虑从前向后地计算 p ,假设我们要计算 \(p_i\),那么由 \(\forall j \in [1,i),p_i\) 已算出
设 l 是目前已经计算过的位置中,向由扩展的最长前缀的首字母的位置,即 l 满足 \(p_l +l\) 最大,记 r 为这个值,显然的有 \(r \ge i-1\)
我们在此时就开始分类 :
part 1
我们讨论 \(r = i - 1\) 的情况,我没在之前没有能利用的信息,于是,直接暴力匹配就好。
part 2
我们讨论 \(r > i - 1\) 的情况。这可就棘手了。当时没听懂 ,首先记 \(j = i - l +1\)
故而我们在做 l 的时候,就知道 \(S_{l\sim i}= T_{1 \sim j}\)
于是,考虑我们要重复匹配的区间,其长度自然是 \(r-i+1\),比较它与 \(z_j\) 的关系,分两种情况讨论
part 2.1
若 \(z_j
于是有 \(p_i=z_j=z_{i-l+1}\)
part2.2
照着前一个 能证明 \(p_i \ge r-i+1\),后面不造故而暴力匹配
然后做 l,r 的的更新即可
而 z 数组的求解无非就是 T 本身的匹配,只要初始化 \(z_1\) 即可
献上代码
#define next z
#define extand p
void Get_Z(){
next[1] = lenb;
for(int i = 2, l = 0, r = 0; i <= lenb; ++i) {
if(i <= r) next[i] = min(next[i - l + 1], r - i + 1);//先看看
while(i + next[i] <= lenb && b[i + next[i]] == b[next[i] + 1]) ++next[i];//然后暴力
if(i + next[i] -1 > r) l = i, r = i + next[i] - 1;//再更新
}
}
void Get_P(){
for(int i = 1, l = 0, r = 0;i <= lena; ++i) {
if(i <= r) extand[i] = min(next[i - l + 1], r - i + 1);
while(i + extand[i] <= lena && a[i + extand[i]] == b[extand[i] + 1]) ++extand[i];
if(i + extand[i] - 1 > r) l = i, r = i + extand[i] - 1;
}
}