知识点
- 卡方分布(Chi-square distribution)
- 四格表资料的卡方检验
- 配对四格表的卡方检验
- 四格表资料的Fisher确切概率法
- 行*列资料的卡方检验
- 多个样本率间的多重比较
- 频数分布拟合优度的卡方检验
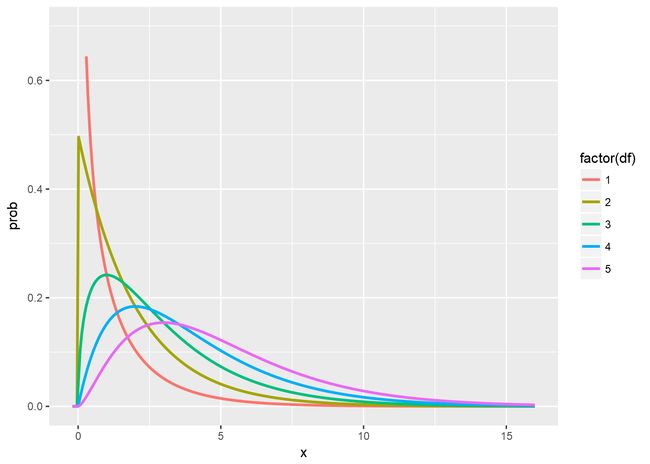
1. 卡方分布
当自由度趋于无穷大时,图形趋于正态分布
# 产生服从卡方分布的观测数为1000的样本
df_n <- seq(1, 5)
chisq_data <- function(n){
x <- seq(-0.2, 16, length=300)
prob <- dchisq(x, df=n[1, 1])
return(data.frame(x=x, prob=prob, df=n[1,1]))
}
require(plyr, quietly=TRUE)
require(ggplot2, quietly=TRUE)
data <- ddply(data.frame(n=df_n), .(n), chisq_data)
head(data)
## n x prob df
## 1 1 -0.20000000 0.000000 1
## 2 1 -0.14581940 0.000000 1
## 3 1 -0.09163880 0.000000 1
## 4 1 -0.03745819 0.000000 1
## 5 1 0.01672241 3.059352 1
## 6 1 0.07090301 1.446043 1
tail(data)
## n x prob df
## 1495 5 15.72910 0.003186504 5
## 1496 5 15.78328 0.003117378 5
## 1497 5 15.83746 0.003049697 5
## 1498 5 15.89164 0.002983433 5
## 1499 5 15.94582 0.002918558 5
## 1500 5 16.00000 0.002855045 5
ggplot(data, aes(x=x, y=prob, color=factor(df), group=df))+geom_line(lwd=1)+scale_y_continuous(limits=c(0, 0.7))
- 其定义为:若n个相互独立的随机变量ξ₁、ξ₂、……、ξn ,均服从标准正态分布(也称独立同分布于 标准正态分布),则这n个服从标准正态分布的随机变量的平方和服从卡方分布
- 可加性:两个服从卡方分布的独立随机变量相加服从自由度为两自由度之和的卡方分布
- 卡方检验的基本思想:由于在假设符合某种情况的前提下,样本实际值偏离理论值的偏差服从正态分布,其均值为理论值,方差也为理论值???(有点疑惑)
2. 四格表资料的卡方检验
书上P98例7-2:表格为
| 组别 | 有效 | 无效 | 合计 |
|---|---|---|---|
| 胞磷胆碱组 | 46 | 6 | 52 |
| 神经节苷酯组 | 18 | 8 | 26 |
| 合计 | 64 | 14 | 78 |
H0:两种药物疗效相同
H1:有效率不等
table7_2 <- matrix(c(46, 18, 6, 8), nrow=2, ncol=2)
chisq.test(table7_2)
## Warning in chisq.test(table7_2): Chi-squared approximation may be incorrect
##
## Pearson's Chi-squared test with Yates' continuity correction
##
## data: table7_2
## X-squared = 3.1448, df = 1, p-value = 0.07617
得到warning "Chi-squared approximation may be incorrect"
因为表格中有T<5, 此时可以采用校正【自动校正】或者fisher.test()
可以用以下代码查看理论值
chisq.test(table7_2)$expected
## Warning in chisq.test(table7_2): Chi-squared approximation may be incorrect
## [,1] [,2]
## [1,] 42.66667 9.333333
## [2,] 21.33333 4.666667
参考:
http://r.789695.n4.nabble.com/In-chisq-test-x-Chi-squared-approximation-may-be-incorrect-td845040.html
3. 四格表资料的Fisher确切概率法
- 超几何分布
从一个有限总体中进行不放回抽样,设N件产品,有M件不合格品,若从中不放回地随机抽取n件,则其中含有的不合格品件数X服从超几何分布,记为X~h(n, N, M)
P100 例7-4组别 感染 未感染 合计 预防组 4 18 22 非预防组 5 6 11 合计 9 24 33
假设两组(预防组和非预防组)的感染率都是9:33【零假设】,则边缘值固定的情况下,相当于在总数33的所有个体中【有9个感染的,24个未感染的】,取22个值作为有效组,在这22个值中,记感染的人数为X,则X~h(22, 9, 24)。
H0: 两个组无查别
# x代表取出来的白球数, k代表取的次数,m代表总白球数,n代表总黑球数
sum(dhyper(x=0:9, k=22, m=9, n=24))
## [1] 1
p_values <- dhyper(x=0:9, k=22, m=9, n=24)
p <- sum(p_values[p_values<=dhyper(x=4, k=22, m=9, n=24)])
print(p)
## [1] 0.1210448
fisher.test(matrix(c(4, 5, 18, 6), nrow=2, ncol=2))
##
## Fisher's Exact Test for Count Data
##
## data: matrix(c(4, 5, 18, 6), nrow = 2, ncol = 2)
## p-value = 0.121
## alternative hypothesis: true odds ratio is not equal to 1
## 95 percent confidence interval:
## 0.03974151 1.76726409
## sample estimates:
## odds ratio
## 0.2791061
4. 配对四格表的卡方检验
- 在次处的配对即同一样本接受两种处理
- 用结果不一致的两种情况计算统计量卡方(分b+c>=40和b+c<40的情况)
- 称为McNemar卡方检验
mat <- matrix(c(11, 2, 12, 33), nrow=2)
# 方法1:
if (mat[1,2]+mat[2,1]>=40) {
x_sq <- (mat[1,2]-mat[2,1])^2/(mat[1,2]+mat[2,1])
}else { x_sq <- (abs(mat[1,2]-mat[2,1])-1)^2/(mat[1,2]+mat[2,1]) }
cat("chi-squareed = ", x_sq,
" p-value = ",
pchisq(x_sq, df=1, lower.tail=FALSE),
sep="")
## chi-squareed = 5.785714 p-value = 0.01615693
# 方法2:
mcnemar.test(mat)
##
## McNemar's Chi-squared test with continuity correction
##
## data: mat
## McNemar's chi-squared = 5.7857, df = 1, p-value = 0.01616
参考:
https://stat.ethz.ch/R-manual/R-devel/library/stats/html/mcnemar.test.html
5. 行*列资料的卡方检验
- 多个样本率的比较(同四格表代码)
样本构成比的比较(同四格表代码)
双向无序分类变量的关联性检验
方法1:
mat <- matrix(
c(431, 388, 495, 137, 490, 410, 587, 179, 902, 800, 950, 32),
nrow=4)
chisq.test(mat)
##
## Pearson's Chi-squared test
##
## data: mat
## X-squared = 213.16, df = 6, p-value < 2.2e-16
x_sq <- chisq.test(mat)$statistic[[1]]
ContCoef <- sqrt(x_sq/(x_sq+sum(mat)))
print(ContCoef)
## [1] 0.1882638
方法2:
# install.packages("DescTools")
mat <- matrix(
c(431, 388, 495, 137, 490, 410, 587, 179, 902, 800, 950, 32),
nrow=4)
DescTools::ContCoef(mat)
## [1] 0.1882638
参考:
https://www.rdocumentation.org/packages/DescTools/versions/0.99.19/topics/Association%20measures
- 双向有序分组变量的线性趋势检验
- 线性趋势:对卡方进行分解,分解为回归分量卡方和偏离线性回归分量卡方
- 相关关系:等级相关分析
- 差别分析:视为单向有序的秩转换非参数检验(如不同年龄组的疗效差别)
- 双向有序属性相同
- 相当为配伍资料(不同检测方法,同一样本)
- 一致性检验(Kappa检验)
- 特殊模型分析
- 单向有序
- 分组为有序,指标为无序(卡方检验)
- 分组为无序,指标为有序(秩转换非参数检验)
6. 多个样本率之间的多重比较
- 卡方分割法
- 多个实验组两两比较(alpha=alpha/(choose(2, k)+1))
- 实验组与同一个对照组比较(alpha=alpha/(2*(k-1)))
7. 频数分布拟合度的卡方检验
- 卡方=sum((理论频数-观察频数)^2/(理论频数))
- 自由度=行数-(计算理论频数时使用的统计量个数如总例数或均数等)