Python深度学习：第4部分

原作者: Jon C-13
链接: https://medium.com/@jon.froiland/python-deep-learning-part-4-ea745ed9cd77

计算机视觉与MNIST的深度学习

我们将深入探讨卷积神经网络（CNN）是什么以及它们为什么在计算机视觉任务中如此成功的理论。但首先，让我们来看看一个简单的CNN例子。它使用CNN对MNIST数字进行分类，这是我们在第一部分和第二部分中使用密集连接网络执行的任务（我们的测试精度当时为97.92%）。即使CNN是最基本的，它的精度也会超出第一部分和第二部分中紧密连接模型的精度。
下面几行代码向您展示了一个基本的CNN是什么样子的。它是一个Conv2D和MaxPooling2D层的堆栈。马上你就会知道他们到底在干什么。

>>> from keras import layers
>>> from keras import models
>>> model = models.Sequential()
>>> model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
>>> model.add(layers.MaxPooling2D((2, 2)))
>>> model.add(layers.Conv2D(64, (3, 3), activation='relu'))
>>> model.add(layers.MaxPooling2D((2, 2)))
>>> model.add(layers.Conv2D(64, (3, 3), activation='relu'))

重要的是，CNN采用形状的输入张量（图像高度、图像宽度、图像通道）（不包括批次维度）。在本例中，我们将配置CNN来处理大小(28, 28, 1)的输入，这是MNIST图像的格式。我们将通过将参数input_shape=(28, 28, 1)传递给第一层来完成这项工作。
让我们展示一下CNN目前的架构：

>>> model.summary()
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_1 (Conv2D)            (None, 26, 26, 32)        320       
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 13, 13, 32)        0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 11, 11, 64)        18496     
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 5, 5, 64)          0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 3, 3, 64)          36928     
=================================================================
Total params: 55,744
Trainable params: 55,744
Non-trainable params: 0
_________________________________________________________________

可以看到，每个Conv2D和MaxPooling2D层的输出都是一个三维形状张量（高度、宽度、通道）。随着网络的深入，宽度和高度维度往往会缩小。通道数由传递给Conv2Dlayers（32或64）的第一个参数控制。
下一步是将最后一个输出张量（形状（3，3，64））输入到一个密集连接的分类器网络中，就像您已经熟悉的那样：一堆Dense层。这些分类器处理一维向量，而当前输出是三维张量。首先我们必须将3D输出平展为1D，然后在顶部添加一些Dense层。

>>> model.add(layers.Flatten())
>>> model.add(layers.Dense(64, activation='relu'))
>>> model.add(layers.Dense(10, activation='softmax'))

我们将做10路分类，使用10个输出和一个softmax激活的最后一层。下面是网络现在的样子：

>>> model.summary()
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_1 (Conv2D)            (None, 26, 26, 32)        320       
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 13, 13, 32)        0         
_________________________________________________________________
conv2d_2 (Conv2D)            (None, 11, 11, 64)        18496     
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 5, 5, 64)          0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 3, 3, 64)          36928     
_________________________________________________________________
flatten_1 (Flatten)          (None, 576)               0         
_________________________________________________________________
dense_1 (Dense)              (None, 64)                36928     
_________________________________________________________________
dense_2 (Dense)              (None, 10)                650       
=================================================================
Total params: 93,322
Trainable params: 93,322
Non-trainable params: 0
_________________________________________________________________

如您所见，（3，3，64）输出在经过两个密集层之前被展平成形状向量（576，）。
现在，让我们训练CNN的MNIST数字。我们将重用第一部分和第二部分中MNIST示例中的许多代码。

>>> from keras.datasets import mnist
>>> from keras.utils import to_categorical
>>> (train_images, train_labels), (test_images, test_labels) = mnist.load_data()
>>> train_images = train_images.reshape((60000, 28, 28, 1))
>>> train_images = train_images.astype('float32') / 255
>>> test_images = test_images.reshape((10000, 28, 28, 1))
>>> test_images = test_images.astype('float32') / 255
>>> train_labels = to_categorical(train_labels)
>>> test_labels = to_categorical(test_labels)
>>> model.compile(optimizer='rmsprop', loss='categorical_crossentropy', metrics=['accuracy'])
>>> model.fit(train_images, train_labels, epochs=5, batch_size=64)
Epoch 1/5
60000/60000 [==============================] - 30s 495us/step - loss: 0.1654 - acc: 0.9481
Epoch 2/5
60000/60000 [==============================] - 29s 480us/step - loss: 0.0458 - acc: 0.9856
Epoch 3/5
60000/60000 [==============================] - 29s 486us/step - loss: 0.0326 - acc: 0.9902
Epoch 4/5
60000/60000 [==============================] - 30s 492us/step - loss: 0.0244 - acc: 0.9927
Epoch 5/5
60000/60000 [==============================] - 30s 495us/step - loss: 0.0189 - acc: 0.9942

让我们根据测试数据评估模型：

>>> test_loss, test_acc = model.evaluate(test_images, test_labels)
10000/10000 [==============================] - 2s 177us/step
>>> test_acc
0.991

而第2部分的密集连接网络的测试准确率为97.92%，而基本CNN的测试准确率为99.1%：我们将错误率降低了57%（相对而言）。不错！
但是，为什么这个简单的CNN与紧密连接的模型相比，工作得那么好呢？为了回答这个问题，让我们深入了解Conv2D和MaxPooling2D层的工作。

卷积运算

密集连接层和卷积层的根本区别在于：密集层在其输入特征空间中学习全局模式（例如，对于MNIST数字，涉及所有像素的模式），而卷积层学习局部模式：对于图像，在输入的小2D窗口中找到的模式。在前面的例子中，这些窗口都是3×3。
图像可以分解为局部图案，如边缘、纹理等。

这个关键特性赋予CNNs两个有趣的特性：

• 他们学习的模式是平移不变的。CNN在图片右下角学习了某个模式后，可以在任何地方识别它：例如，在左上角。如果一个紧密连接的网络出现在一个新的位置，它就必须重新学习这个模式。这使得CNNs数据在处理图像时高效（因为视觉世界基本上是平移不变的）：它们需要较少的训练样本来学习具有泛化能力的表示。
• 他们可以学习模式的空间层次结构。第一卷积层将学习小的局部模式，例如边缘，第二卷积层将学习由第一层的特征构成的更大的模式，等等。这使得CNNs能够有效地学习越来越复杂和抽象的视觉概念（因为视觉世界基本上是空间层次的）。
  视觉世界形成了视觉模块的空间层次结构：超局部边缘组合成眼睛或耳朵等局部对象，这些对象组合成“猫”等高级概念。
  卷积在三维张量（称为特征映射）上操作，具有两个空间轴（高度和宽度）和一个深度轴（也称为通道轴）。对于RGB图像，深度轴的尺寸为3，因为图像有三个颜色通道：红色、绿色和蓝色。对于黑白图片，如MNIST数字，深度为1（灰度级别）。卷积操作从其输入特征映射中提取方块(patch)，并对所有这些方块(patch)应用相同的变换，生成输出特征映射。这个输出特性图仍然是一个三维张量：它有一个宽度和一个高度。它的深度可以是任意的，因为输出深度是层的一个参数，并且深度轴中的不同通道不再代表RGB输入中的特定颜色；相反，它们代表过滤器。过滤器对输入数据的特定方面进行编码：例如，在较高的级别上，单个过滤器可以对“输入中存在一个面”的概念进行编码。
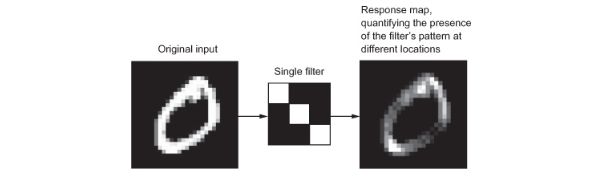
  在MNIST示例中，第一卷积层采用大小为（28、28、1）的特征映射并输出大小为（26、26、32）的特征映射：它在其输入上计算32个滤波器。这32个输出通道中的每一个都包含一个26×26的值网格，它是输入上的滤波器的响应图，指示该滤波器模式在输入中不同位置的响应。这就是术语特征映射的意思：深度轴中的每个维度都是一个特征（或过滤器），而2D张量输出[：，：，n]是该过滤器对输入的响应的2D空间映射。
  响应图的概念：输入中不同位置存在模式的二维图。

卷积由两个关键参数定义：

• 从输入中提取的方块(patch)大小 — 它们通常是3×3或5×5。在这个例子中，它们是3×3，这是一个常见的选择。
• 输出特征映射的深度 — 由卷积计算出的滤波器数目。示例以32的深度开始，以64的深度结束.
  在Keras Conv2D图层中，这些参数是传递给图层的第一个参数： Conv2D(output_depth, (window_height, window_width)).
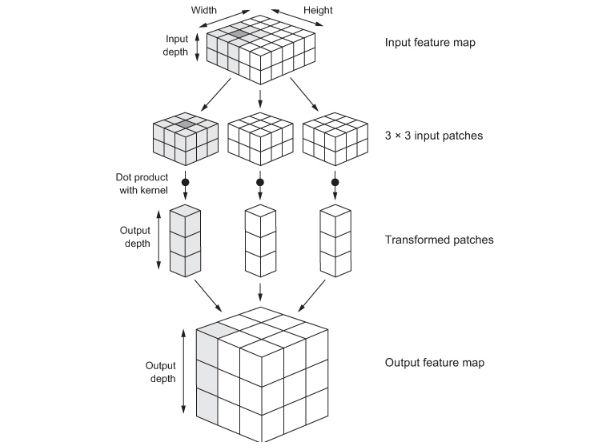
  卷积的工作原理是将这些大小为3×3或5×5的窗口滑动到三维输入特征图上，在每个可能的位置停止，并提取周围特征的三维方块(patch)（形状（窗口高度、窗口宽度、输入深度））。然后，每个这样的三维方块(patch)（通过具有相同学习权矩阵的张量积，称为卷积核）被转换为一维形状向量（输出深度）。然后，所有这些矢量在空间上重新组合成一个形状（高度、宽度、输出深度）的三维输出地图。输出特征映射中的每个空间位置对应于输入特征映射中的相同位置（例如，输出的右下角包含有关输入的右下角的信息）。例如，对于3×3窗口，矢量输出[i, j, :]来自3D方块(patch)输入[i-1:i+1, j-1:j+1, :]。

卷积是如何工作的

请注意，输出宽度和高度可能与输入宽度和高度不同。它们可能有两个不同的原因：

• 边界效果，可以通过填充输入特征映射来抵消。
• 步长(stride)的使用，我将在第二部分中定义，让我们更深入地了解这些概念。

了解边界效果和填充

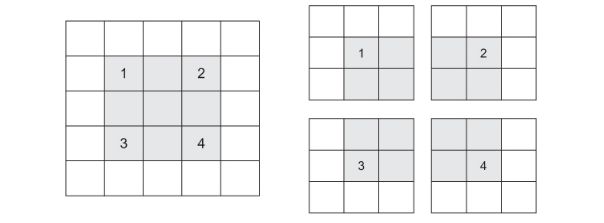
考虑一个5×5的特征图（总共25个分幅）。只有9块瓷砖可以将一个3×3的窗口居中，形成一个3×3的网格。

5×5输入特征图中3×3方块(patch)的有效位置

因此，输出特征图为3×3。它缩小了一点：在本例中，每个维度旁边正好有两个平铺。在前面的例子中可以看到这种边界效应的作用：从28×28个输入开始，在第一个卷积层之后变成26×26。
如果要获得与输入具有相同空间维度的输出要素地图，可以使用填充(padding)。填充包括在输入特征映射的每一侧添加适当数量的行和列，以便能够在每个输入平铺周围适应中心卷积窗口。对于3×3窗口，可以在右侧添加一列，在左侧添加一列，在顶部添加一行，在底部添加一行。对于5×5的窗口，可以添加两行。

填充5×5的输入以便能够提取25个3×3的方块(patch)

在Conv2D层中，padding可以通过padding参数进行配置，该参数接受两个值：“valid”，这意味着没有padding（只使用有效的窗口位置）；和“same”，这意味着“padd的输出宽度和高度与输入相同。”padding参数默认为“valid”。

理解卷积步长(stride)

影响产出规模的另一个因素是步长的概念。目前对卷积的描述假定卷积窗口的中心块都是连续的。但是两个连续窗口之间的距离是卷积的一个参数，称为它的步长，默认为1。可能有步长卷积：步长大于1的卷积。

2×2步长的3×3卷积方块(patch)

您可以看到通过3×3卷积和步长2在5×5输入（无填充）上提取的方块(patch)。
使用“步幅2”意味着特征地图的宽度和高度将按系数2（除了由边界效果引起的任何更改）进行下采样。跨步卷积在实践中很少使用，尽管它们在某些类型的模型中很有用；熟悉这个概念很好。
为了降低特征地图的采样率，我们倾向于使用最大池化(max pooling)操作，您在第一个CNN示例中看到了这个操作。让我们更深入地研究一下。

最大池化操作

在CNN的例子中，您可能已经注意到，在每个MaxPooling2D层之后，特征地图的大小减半。例如，在第一个MaxPooling2D层之前，特征映射为26×26，但是max pooling操作将其减半为13×13。这就是最大池化的作用：积极降低样本特征映射，非常像快速卷积。
最大池包括从输入特征映射中提取窗口并输出每个通道的最大值。它在概念上类似于卷积，除了不通过学习的线性变换（卷积核）变换局部方块(patch)，而是通过硬编码的最大张量运算进行变换。与卷积的一大区别是，最大池通常使用2×2窗口和步长2来完成，以便将特征映射的采样率降低2倍。另一方面，卷积通常是用3×3窗口和无步长（步长1）完成的。
为什么要用这种方式绘制特征地图？为什么不删除最大池层，并保持相当大的功能地图一直向上？让我们看看这个选项。模型的卷积基将如下所示：

>>> model_no_max_pool = models.Sequential()
>>> model_no_max_pool.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
>>> model_no_max_pool.add(layers.Conv2D(64, (3, 3), activation='relu'))
>>> model_no_max_pool.add(layers.Conv2D(64, (3, 3), activation='relu'))

以下是模型的摘要：

>>> model_no_max_pool.summary()
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_4 (Conv2D)            (None, 26, 26, 32)        320       
_________________________________________________________________
conv2d_5 (Conv2D)            (None, 24, 24, 64)        18496     
_________________________________________________________________
conv2d_6 (Conv2D)            (None, 22, 22, 64)        36928     
=================================================================
Total params: 55,744
Trainable params: 55,744
Non-trainable params: 0
_________________________________________________________________

这个模型怎么了？两件事：

• 它不利于学习特征的空间层次结构。第三层的3×3窗口只包含初始输入中来自7×7窗口的信息。CNN学习到的高级模式对于初始输入来说仍然是非常小的，这可能不足以学会对数字进行分类（试着只通过7×7像素的窗口来识别一个数字！）。我们需要来自最后一个卷积层的特征来包含关于输入整体的信息。
• 最终的特征映射为每个样本22×22×64=30976个总系数。这是巨大的。如果你把它放平，在上面贴上一个512大小的Dense层，这个层将有1580万个参数。这对于这样一个小模型来说太大了，会导致强烈的过度拟合。
  简而言之，使用下采样的原因是减少要处理的特征映射系数的数量，以及通过使连续卷积层看着越来越大的窗口（根据它们覆盖的原始输入的分数）来诱导空间滤波器层次。
  注意，最大池并不是实现这种向下采样的唯一方法。正如您已经知道的，您还可以在前面的卷积层中使用steps。您可以使用平均池而不是最大池，其中每个本地输入方块(patch)通过获取方块(patch)上每个通道的平均值而不是最大值进行转换。但是最大池往往比这些替代解决方案工作得更好。简而言之，原因是特征倾向于在特征地图的不同分幅上编码某个模式或概念的空间存在（因此，术语特征地图），并且观察不同特征的最大存在比观察它们的平均存在更有信息量。因此，最合理的子抽样策略是首先生成特征的稠密映射（通过非有向卷积），然后在小方块(patch)上查看特征的最大激活，而不是查看输入的稀疏窗口（通过有向卷积）或平均输入方块(patch)，这可能会导致您丢失或稀释功能状态信息。
  在这一点上，你应该了解CNN的基本知识-特征映射，卷积和最大池-你知道如何建立一个小型CNN来解决一个玩具问题，如MNIST数字分类。现在让我们继续讨论更有用、更实际的应用。

Chollet, François. Deep learning with Python. Shelter Island, NY: Manning Publications Co, 2018. Print.