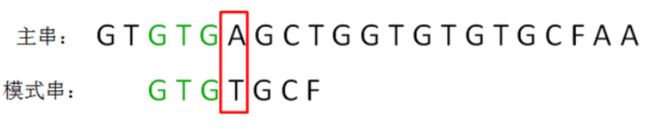一、基本概念
数据结构中提到的串,即字符串,由 n 个字符组成的一个整体( n >= 0 )。这 n 个字符可以由字母、数字或者其他字符组成。
特殊的串
- 空串:含有零个字符的串
- 空格串:只包含空格的串。注意和空串区分开,空格串中是有内容的,只不过包含的是空格
- 子串与主串:串中任意个连续字符组成的字符串叫做该串的子串,包含子串的串称为主串。
串的存储形式
- 定长顺序存储
这个很好理解,采用固定长度的数组(即静态数组)存储串。
char a[20];
- 堆分配存储
在C语言中,存在着一个被称之为“堆”的自由存储区,用 malloc 函数和 free 函数管理,malloc 函数负责申请空间,free 函数负责释放空间。
char *a= (char*)malloc(20*sizeof(char)); 申请了20个char字符空间
当空间不够大时,可以用realloc函数重新申请更大的存储空间。
a = (char*)realloc(a, 50*sizeof(char));
//前一个参数指申请空间的对象;第二个参数,重新申请空间的大小
- 块链存储
#define size 10
struct string_node{
char s[size];
string_node *next;
};
struct String //标记头尾指针,和长度
{
string_node* head, * tail;
int length;
};
使用块链储存时,会有节点大小问题。存储多个字符,会导致操作苦难,存储一个会导致浪费空间。
二、BF匹配算法
判断两个串是否存在子串与主串的关系,最直接的算法就是拿着模式串,去和主串从头到尾一一比对,这就是“BF”算法的实现思想。
int BF(char s[], char t[])
//返回子串t在主串S中字符之后的位置。若不存在,则函数值为0。
{
for (int i = 0; i < strlen(s); i++)
{
int flag = 0;
for (int j = 0; j < strlen(t); j++)
if (s[i + j] != t[j]) {
flag = 1;
break;
}
if (flag == 0) {
cout << i+1 << endl;//加一补足
return i+1;
}
if (i + strlen(t) > strlen(s))
return 0;
}
}
时间复杂度为O(M*N)
整个算法其实就循环执行如下两个步骤:
- 从每一轮的基准点开始比较两个字符串;
- 如发现不能完全匹配目标字符串,将目标字符串向后挪动一个字符的位置(即更新基准点);
三、KMP算法
而KMP算法可以充分利用模式串的部分匹配信息,保持主串i指针不变(不需要回溯主串),通过修改模式串j指针(变动的是模式串下标),让模式串尽量移动到有效的位置,以减少比较次数。可以实现算法时间复杂度为O(m+n)。
例子:
KMP算法和BF算法的“开局”是一样的,同样是把主串和模式串的首位对齐,从左到右对逐个字符进行比较。
第一轮,模式串和主串的第一个等长子串比较,发现前5个字符都是匹配的,第6个字符不匹配,
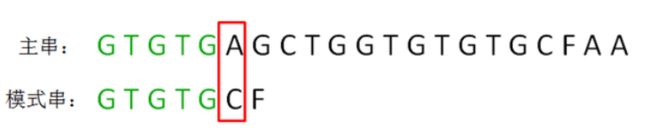
这时候,如何有效利用已匹配的前缀 “GTGTG” 呢?
我们可以发现,在前缀“GTGTG”当中,后三个字符“GTG”和前三位字符“GTG”是相同的:
在下一轮的比较时,只有把这两个相同的片段对齐,才有可能出现匹配。这两个字符串片段,分别叫做最长可匹配后缀子串和最长可匹配前缀子串。
第二轮,我们直接把模式串向后移动两位,让两个“GTG”对齐,继续从刚才主串的坏字符A开始进行比较:
显然,主串的字符A仍然是坏字符,这时候的匹配前缀缩短成了GTG:
按照第一轮的思路,我们来重新确定最长可匹配后缀子串和最长可匹配前缀子串:
第三轮,我们再次把模式串向后移动两位,让两个“G”对齐,继续从刚才主串的坏字符A开始进行比较:
以上就是KMP算法的整体思路:在已匹配的前缀当中寻找到最长可匹配后缀子串和最长可匹配前缀子串,在下一轮直接把两者对齐,从而实现模式串的快速移动。
这里我们引入一个数组next[]。
这是一个一维整型数组,数组的下标代表了“已匹配前缀的下一个位置”,元素的值则是“最长可匹配前缀子串的下一个位置”。
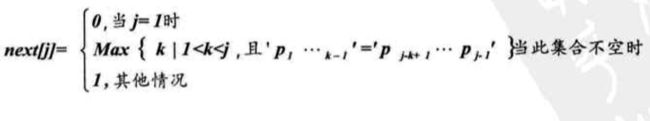
我推荐看 这个视频 ,或者博客来深刻理解next数组。
int n[256];
int get_next(char s[])
{
int j = 0;
int k = -1;
n[0] = -1;
while (j < strlen(s)) {
if (k == -1 || s[j] == s[k]) {
//s[k]代表前缀的单个字符,s[j]代表后缀的单个字符
//,此时的 k 即是相同子串的长度
j++, k++;
n[j] = k;
}
else
k = n[k];
//保留了配对失败时的此时前缀字符的k值,方便回溯
}
cout << endl;
return 0;
}
有了next数组,写出KMP算法就容易多了。
int KMP(char a[], char s[])
{
int i = 0, j = 0;
get_next(s);
int length_a = strlen(a);
//切记不要使用strlen在条件判断中
int length_s = strlen(s);
while (i