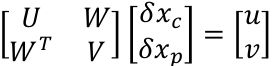综述
在开始介绍自己的框架之前,先总结一下通用的视觉里程计框架(直接法和特征点法),看看一个视觉里程计系统都需要什么样的模块,一个可以让SLAM运行起来的最小系统是怎样的。
然后再来仔细全面的剖析一下我们现有的VIO框架是怎样实现的,以及有哪些模块是必要的,有哪些模块是可以被替换的,还有哪些模块必须要进行加速以及加速的具体方法.
最后设计一个VIO框架(Vision-Inertial Odometry)实时性要求:(前端+后端串行 (i7两个cpu核,gtx1060 gpu)100HZ左右)鲁棒性要求:(在图像纹理不丰富、纹路重复、曝光引起亮度变化或者相机快速运动、纯旋转以及动态物体遮挡的情况下不跟丢,恢复真实相机位姿)
特征点法(稀疏光流跟踪)
所谓特征点法,就是利用光流或者特征描述子等方法在图像上进行特征点提取和跟踪,然后使用每一帧图像中已知跟踪的特征点的图像坐标,利用反投影误差优化相机位姿和特征点深度。描述子匹配的方法因为太过于耗时,这里不予讨论。具体过程如下图所示:
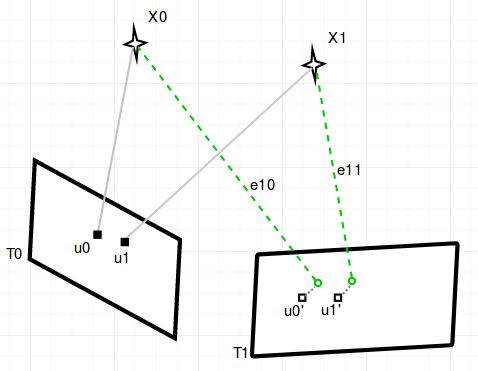
如上图1.1所示,假设T0时刻相机第一次观测到在三维空间中的点X0和X1,它们投影在二维图像上的坐标为u0,u1,是两维的(后续称为KeyPoint_Source,简称)。
接下来使用LK光流法计算u0,u1在T1时刻相机的图像中位置为u0’和u1‘(后续称,i代表图像帧的序列号)。
e10,e11为T1时刻的两次在图像上的观测残差,即预测的图像点坐标和跟踪的图像点坐标的距离,每个观测包含一个和一个(后续简称)
我们想求解的是,相机T0和T1相对坐标系原点的,以及X0,X1在T0时刻的深度(后续简称),那么只需要最小化:
(1.0)
其中 为所有的待估计变量,观测残差可以写成如下公式(1.1)形式,具体这个最优化怎么解我们后面再具体分析,现在只需要知道这个最优化问题的复杂程度是根据误差项的多少成指数增长的。
(1.1)
下面来看光流法是如何跟踪特征点的,我们先以位于u0处的像素为例,它的灰度在t时刻下可以写成:
光流法有一个灰度不变假设,即同一个像素点在各帧图像中的灰度值是固定不变的,当然这在现实中会有很多失效的情况比如曝光时间变化或者光照变化、阴影等等,这里省略光流跟踪中的技巧,暂且认为假设(1.2)成立:
(1.2)
对左边进行泰勒展开,保留一阶,得:
(1.3)
我们假设了灰度不变,所以泰勒展开的一阶项为0,再除以dt,得:
(1.4)
矩阵形式为:
其中的为图像在x方向的梯度,为图像在y方向梯度,图像灰度对时间的变化量为,u,v是u0像素在x,y轴的运动速度,上面的公式只是一个像素点的,我们构建一个在u0附近的窗口,假设这个窗口内的像素运动速度相同,我们可以列出个这样的公式,这是一个关于u,v的超定方程使用最小二乘解法即可。
至此,基于稀疏光流的纯视觉里程计就介绍完毕了,这里面涉及的前后端基本可以构成一个视觉里程计系统,但是因为单目视觉缺乏尺度和初始点云的深度信息,初始化系统就是用来完成这一部分的工作,这个在后面会具体介绍。
除此之外,我们经常使用一个窗口来优化特征点,窗口中的图像帧不一定是按照时间序列排列的最近的几帧,而是经过挑选的”关键帧“,这些关键帧往往互相之间在时间上或者空间上间隔较远,有足够的”视差“,并且能跟当前帧共享很多特征点。既然有窗口就涉及到旧的图像帧和特征点需要被marg out,在slam问题里叫做边缘化,我们希望被边缘化的点和图像帧还能保留住它的信息,但是整个优化方程始终维持一个固定的海森矩阵,这在后面也会详细讲解。
光流跟踪特征点法优缺点总结。优点如下:
1.前端特征提取和后端优化是完全解耦。这样前端和后端互不影响,前端特征点不会因为偶发的后端优化失败而跟踪失败。
2.时间消耗极少。通过我们的实验,一般需要跟踪的特征点在100个左右时,只需要不到1ms。
缺点:
1.图像的非凸性。图像的梯度在整张图中是“坑坑洼洼”的,如果只采用图像梯度进行特征点跟踪,最后的优化迭代很容易进入极小值,只有在运动很小时才能起作用。在运动过快或者有重复纹理的情况下,光流法很容易误匹配或者跟丢。
2.边缘像素没有区分度。如果在边缘附近提取了特征点,那么光流法的跟踪结果会在边缘“滑动”导致误匹配。
3.灰度不变是强假设。如果相机是自动曝光的,调整曝光参数时,图像整体会变亮变暗,光照变化时也会出现这种情况,这时光流法会大概率整张图全部跟丢。
直接法(稀疏直接法)
所谓直接法slam,求解的问题跟特征点法是一致的,都是相机位姿和sourceFrame的特征点深度,跟特征点法最大的不同在于残差项不再是图像平面的像素距离,而是光度误差,而且前端后端没有明显的分界,是耦合在一起的。当调整待优化变量到满足光度误差总体最小时,帧间特征匹配也做完了。如下图2.1所示,由于没有特征匹配,无法知道u0,u1对应的T1时刻相机平面上的哪两个点,但是如果相机位姿或者特征点深度优化的不好,投影到T1的u0’的外观和u0会有明显区别。
于是,我们采用光度误差来代表一次观测误差:
(2.1)
值得注意的是,跟特征点法不同,在计算雅克比矩阵时,会在最外层多乘以一个,即图像在u处的x,y方向的梯度。
与特征点法的不同,直接点法直接利用图像中梯度变化明显的边缘和交点,动则每帧会有成百上千个特征点会参与优化,如果是每个像素点都要加入优化中,就是稠密直接法,稠密法一般一次优化会有几十万条边,需要借助GPU才能勉强计算。而稀疏直接法每次参与优化的点可以在1000个以内,为了实时性需求可以更少。
直接法节省了前端匹配时间,在实际应用中可以只用CPU做到非常快速的效果,经过测试,调整分辨率和参数之后,DSO可以在地下停车场场景跑到80hz(i7 cpu单核)而不牺牲精度。
直接直接点法优缺点总结。优点如下:
1.可以省去计算特征点的时间
2.图像只要求有像素梯度即可,不需要特征点一一对应,即使在纹理大范围缺失的地方(楼梯间,高速公路)下也能估计出相机的位姿变化。
3.可以构建稠密或者半稠密的地图,这是特征点法不可能实现的。
VIO框架,公式原理
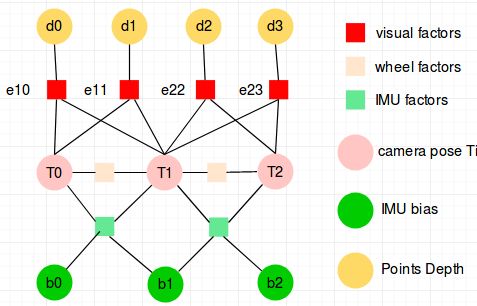
现有VIO框架主要是在特征点法的基础上加上imu的旋转约束和车速的平移约束,如下图3.1所示,加入imu和车速的意义在于,可以hold住视觉不适应的场景,比如曝光时间突变,相机运动过快,动态障碍物遮挡等等。
在整个优化问题里面加入IMU和车速的方式也是通过增加新的观测残差来实现,比如上图中的e_imu01残差项是指T0到T1时刻相机的相对旋转R与imu在这段时间的陀螺仪积分R做差,e_wheel01残差项是指T0到T1时刻相机的相对平移t与车速在这段时间的积分t做差,具体公式如3.1,3.2,其中为imu到相机的外参,为轮轴中心到相机的外参,为imu在T0到T1时刻的预积分:
(3.1)
(3.2)
整个优化方程从公式(1.0)变为公式(3.3):
(3.3)
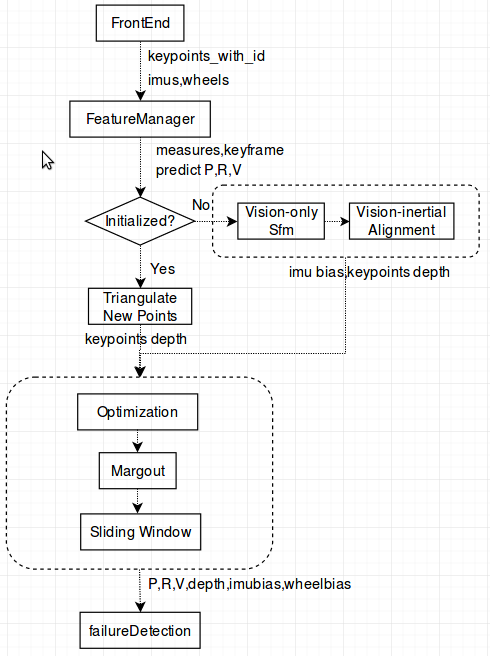
整个vio的后端运行框架如下图3.2所示,前端负责检测特征点提取和跟踪以及imu、车速的预积分。特征管理模块负责生成特征观测残差、imu预积分残差和关键帧提取,初始化模块负责生成恢复了真实尺度的初始点云以及初始相机位姿,三角化模块负责对新增的特征点赋予深度信息,优化模块负责解公式(3.3),边缘化模块负责弹出旧的图像帧和不在图像中的特征点并构建新的”边缘化先验约束“,滑动窗口模块负责把所有观测数据维持在一个窗口内,最后的错误检测模块负责检测优化结果是否符合预期,如果不符合预期则重新初始化。
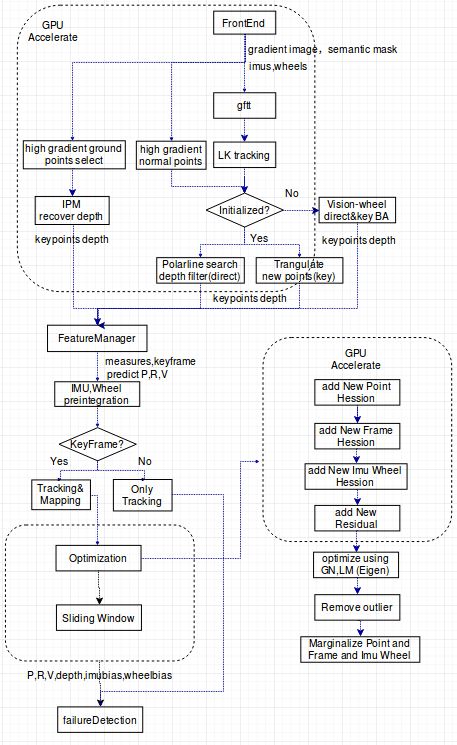
上图3.2所示的框架是开源项目VINS的框架,它能在大部分场景运行良好,缺点是对图像边缘信息不够敏感,如果整张图中只剩下一些边缘和线特征,跟踪往往会失败。而且上述框架对系统cpu资源要求比较高,无法在cpu资源受限的场景下实时运行(A57等低端Arm芯片)。所以我们提出如图3.3所示的框架,融合了直接法和特征点法,并且不使用类似g20或者ceres这类的优化库,在可以并行的模块上使用GPU或者FPGA并行,使得整个VIO快速运行在并行运行资源多于CPU资源的硬件平台上(TX2,FPGA板子)。接下来会着重介绍新框架的具体细节。
视觉惯导联合初始化
对于单目视觉VIO来说,初始化模块是整个系统至关重要的一环。初始化模块负责提供给系统初始图像的位姿和初始图像所有特征点的深度,并且特征点深度是恢复了真实尺度的。对于VIO来说,初始化模块往往还需要求解出重力方向,每一帧的三维速度以及IMU陀螺仪的bias。但是如果系统不使用IMU的加速度计并且有车速的话,那么重力方向是可以省略不去关注的。
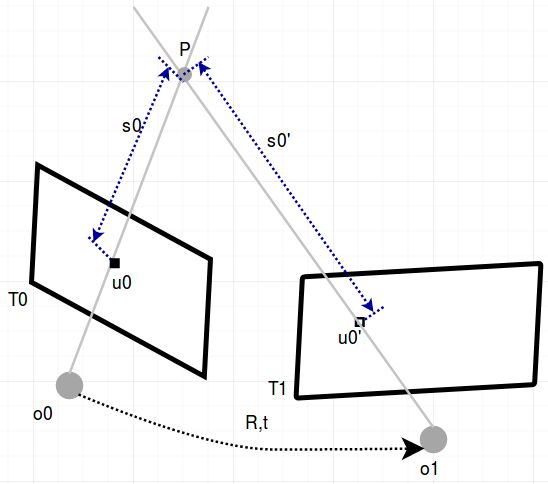
我们这里只讨论不使用IMU加速度计的VIO初始化。首先,如果两帧之间的共同观测和视差大于一定的阈值,我们就把这两帧作为初始化的第一帧和第二帧。接下来通过IMU和车速的积分,我们可以知道前两帧图像之间的粗略旋转平移。这时问题就变成了如何从两张已知位姿的二维图像获得图像上的特征点深度。这是一个典型的”三角化“问题,如图3.3所示,有两帧图像同时观测到点P,已知帧间R,t和相机光心位置o1和o2,需要优化点P的三维位置,使得如下公式(3.4)成立,其中u0,u0‘为像素点的三维归一化平面坐标是已知的,s0,s0’为我们要求解的深度:
(3.4)
如果我们对等式两边都乘以u0的反对称矩阵,公式等号左边为零,等号右边只有未知数s0',这样我们直接可以算出s0‘的值,由此,我们可以算出前两帧图像上所有特征点的深度。
虽然通过上面的步骤,我们得到了特征点深度图,但是我们的R,t和特征点的跟踪都是有误差的,所以这个深度只能当做初值,在接下来的第2,3,4....帧当中,我们会选取一定数量的关键帧来共同参与到这个三角化的过程,也就是把每一帧新三角化成功的点分别投影到其他关键帧中建立最小二乘,重复这个过程。最后利用公式(3.3)建立一个BandleAjustment问题,用GN或者LM方法求解非线性优化问题,最终求解出最优的相机位姿和特征点深度。
在实际工程当中,我们更相信视觉解算出的角度和原始车速,所以在初始化求解公式(3.3)时,我们通常把imu陀螺仪涉及的误差项去掉,并且在求解完毕之后再用求解出的相机帧间旋转关系最小化公式(3.1)求解IMU陀螺仪的bias。这样就完成了整个初始化过程。
特征点法和直接法联合初始化
上面介绍的是用特征点法进行初始化的过程。但是在我们实际项目当中,也需要用到图像中具有丰富梯度信息的”边缘特征点“。这类特征点不可能直接在图像中找到前后帧的对应关系,需要我们用图2.1所示的那样使用光度误差来迭代优化特征点的深度和相机位姿,但是实际工程中,直接法很难从两张图像用迭代优化的方法初始化成功,导致整个系统一直在重复进行初始化,这里我们结合特征点法容易初始化的特点,设计如下直接法初始化方法:
1.首先进行纯特征点法初始化,同时使用直接法选取关键帧图像上梯度变化明显的稀疏点(2000个左右)
2.待特征点法初始化成功,我们可以得到两帧图像之间的准确位姿和一个窗口内稀疏的恢复了深度的特征点(100个左右),这时我们可以把每个直接法提取的特征点赋予一个深度初值,赋值的原则是,对于已经恢复了深度的稀疏特征点周围w*w窗口范围内的点深度都等于它本身。
3.经过上面的步骤,大部分没有深度的特征点都被赋予了初始深度,这时我们再用极线搜索方法把恢复了初始深度的特征点投影到每一个关键帧图像中搜索最匹配的像素块使用深度滤波器更新一下深度。
4.最后再用高斯牛顿法最小化公式(3.3),其中的视觉观测误差同时包含公式(1.1)和公式(2.1)。使得所有窗口内的直接法特征点的反投影光度误差之和最小和特征点法提取额的特征点投影误差最小。
IMU陀螺仪预积分
非关键帧跟踪
经过上述系统初始化之后,我们开始处理视频流,当一个新图像帧系统进入之后,我们首先对它进行特征提取,并使用一些方法来判断当前帧是否为关键帧(下节会详细说明),如果是非关键帧,我们就把上一个关键帧优化好深度的地图点投影到当前帧并使用高斯牛顿法最小化公式(3.3),只优化当前帧涉及到的特征点深度和当前帧位姿并直接输出位姿结果,不需要进行后面的紧耦合优化,也不需要参与海森矩阵的更新,所以速度很快。
关键帧跟踪并生成新三维点
选取关键帧的方法主要有以下标准,满足其中任何一项即可认定为关键帧:
1. 与最近的关键帧之间的视差大于一定阈值(用光流法看所有特征点一共移动多少像素)
2.与最近关键帧之间的平移距离大于一定阈值(用轮速+IMU)
3.使用直接法tracking时的光度误差增大一定阈值(一般在光照变化或者快速旋转时)
4.在进行上一步跟踪时,跟踪上的特征点个数大于一定阈值(特征丰富,可以在后续提供更多共视的特征点)
一旦确认了关键帧,我们先使用非关键帧跟踪一样的策略优化当前帧位姿和旧特征点深度,之后再把当前关键帧新产生的特征点更新到地图当中,并标记成未成熟。接下来对地图中所有未成熟点赋予初始深度,采用跟初始化时一样的策略,即把特征点投影到当前帧看有没有共同观测,如果有,就看投影到其他关键帧是否有共同观测,如果观测帧数大于一定阈值就把未成熟点激活。需要注意一下,在优化之前当前关键帧新生成的未成熟点不会被激活。接下来,系统进入优化模块。
紧耦合优化
所谓的紧耦合优化就是在一个关键帧窗口内,同时优化窗口内所有的关键帧位姿和特征点深度以及IMU陀螺仪Bias。整体误差项如公式(3.5)。每一帧的待优化变量为:
其中为相机的位姿,b为IMU陀螺仪Bias,d为特征点深度。这是一个典型的非线性优化问题,解这个公式通常使用ceres或者g2o这类专门的优化库,但是我们如果需要加速vio就必须要自己用矩阵构建整个优化问题。
(3.5)
以高斯牛顿法为例,求解优化变量的增量方程可以写为:
(3.6)
其中J为残差e关于整体优化变量X的Jacobian,上式可以简写成,其中H为近似的海森矩阵,公式(3.6)可以写成矩阵形式:
求解上述增量方程时,常采用的方法是Schur Complement,即先边缘化掉路标点,可得:
(3.7)
上式可以简化为,S是表示相机之间共视关系的矩阵,通常对于滑动窗口来说S是稠密的,即两两相机之间都能看到相同的路标点。
以图3.1为例,残差项对变量的Jacobian如下表表示,其中T代表相机位姿,B代表IMU Bias,s代表特征点深度:
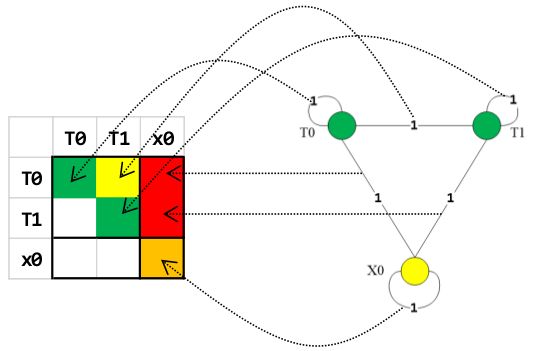
因子图如下图3.6所示,所谓因子图就是把每一项观测误差当成为图中的一个节点,把跟这次观测相关的待优化变量当成图中一个边,可以方便的看出每个误差项(也叫因子factor)对各种待优化变量的关系。
基于上面的因子图,我们可以方便的知道每个factor对雅克比矩阵块的影响,同时也能知道没有factor对海森矩阵块的影响:即与小方块相连的所有变量的两两之间,自己和自己之间,都添加一个边,边上的数字表示有几个约束会同时影响海森矩阵中该处的值,如下图3.7所示为视觉factor对海森矩阵的影响。
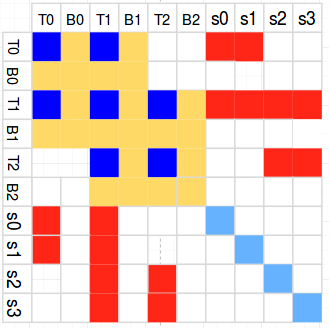
可以看到应用上面的因子图方法,海森矩阵的T1行T1列的这个块受到八项factor影响。以此类推,整个因子图对应的整个海森矩阵如下图所示,其中深蓝色块代表同时受视觉、IMU、车速影响的矩阵块,黄色块代表只跟IMU有关的矩阵块,红色和浅蓝只跟视觉有关:
增加新关键帧到海森矩阵
对于新被选成关键帧的图像需要加入到整个优化框架中,对于跟这帧数据相关的所有优化变量都会有影响,对应的海森矩阵也是有所影响,我们以T1时刻增加一帧关键帧为例,加入T1关键帧对各个优化变量如下图所示:
其中以海森矩阵块中的为例,公式如下图公式:
GN优化
边缘化点
边缘化帧
边缘化关键帧策略:
1. 总是保留最近的两帧关键帧
2. 与最近关键帧之间的共视特征点少于5%就需要被边缘化
3. 关键帧需要在三维空间内尽量均匀分布,但是需要保证最近的关键帧附近有更多的关键帧
设计高速VIO
前端GPU加速
后端CPU加速
后端GPU加速
参考文献:
[1] Raúl Mur-Artal, J. M. M. Montiel and Juan D. Tardós.ORB-SLAM: A Versatile and Accurate Monocular SLAM System.IEEE Transactions on Robotics,vol. 31, no. 5, pp. 1147-1163, 2015. (2015 IEEE Transactions on RoboticsBest Paper Award).
[2] Dorian Gálvez-López and Juan D. Tardós.Bags of Binary Words for Fast Place Recognition in Image Sequences.IEEE Transactions on Robotics,vol. 28, no. 5, pp. 1188-1197, 2012.