LeetCode:N-Queens I II(n皇后问题)
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle.
Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.
For example,
There exist two distinct solutions to the 4-queens puzzle:
[ [".Q..", // Solution 1 "...Q", "Q...", "..Q."], ["..Q.", // Solution 2 "Q...", "...Q", ".Q.."] ]
算法1
这种棋盘类的题目一般是回溯法, 依次放置每行的皇后。在放置的时候,要保持当前的状态为合法,即当前放置位置的同一行、同一列、两条对角线上都不存在皇后。
class Solution {
private:
vector<vector<string> > res;
public:
vector<vector<string> > solveNQueens(int n) {
vector<string>cur(n, string(n,'.'));
helper(cur, 0);
return res;
}
void helper(vector<string> &cur, int row)
{
if(row == cur.size())
{
res.push_back(cur);
return;
}
for(int col = 0; col < cur.size(); col++)
if(isValid(cur, row, col))
{
cur[row][col] = 'Q';
helper(cur, row+1);
cur[row][col] = '.';
}
}
//判断在cur[row][col]位置放一个皇后,是否是合法的状态
//已经保证了每行一个皇后,只需要判断列是否合法以及对角线是否合法。
bool isValid(vector<string> &cur, int row, int col)
{
//列
for(int i = 0; i < row; i++)
if(cur[i][col] == 'Q')return false;
//右对角线(只需要判断对角线上半部分,因为后面的行还没有开始放置)
for(int i = row-1, j=col-1; i >= 0 && j >= 0; i--,j--)
if(cur[i][j] == 'Q')return false;
//左对角线(只需要判断对角线上半部分,因为后面的行还没有开始放置)
for(int i = row-1, j=col+1; i >= 0 && j < cur.size(); i--,j++)
if(cur[i][j] == 'Q')return false;
return true;
}
};
算法2
上述判断状态是否合法的函数还是略复杂,其实只需要用一个一位数组来存放当前皇后的状态。假设数组为int state[n], state[i]表示第 i 行皇后所在的列。那么在新的一行 k 放置一个皇后后:
- 判断列是否冲突,只需要看state数组中state[0…k-1] 是否有和state[k]相等;
- 判断对角线是否冲突:如果两个皇后在同一对角线,那么|row1-row2| = |column1 - column2|,(row1,column1),(row2,column2)分别为冲突的两个皇后的位置
class Solution {
private:
vector<vector<string> > res;
public:
vector<vector<string> > solveNQueens(int n) {
vector<int> state(n, -1);
helper(state, 0);
return res;
}
void helper(vector<int> &state, int row)
{//放置第row行的皇后
int n = state.size();
if(row == n)
{
vector<string>tmpres(n, string(n,'.'));
for(int i = 0; i < n; i++)
tmpres[i][state[i]] = 'Q';
res.push_back(tmpres);
return;
}
for(int col = 0; col < n; col++)
if(isValid(state, row, col))
{
state[row] = col;
helper(state, row+1);
state[row] = -1;;
}
}
//判断在row行col列位置放一个皇后,是否是合法的状态
//已经保证了每行一个皇后,只需要判断列是否合法以及对角线是否合法。
bool isValid(vector<int> &state, int row, int col)
{
for(int i = 0; i < row; i++)//只需要判断row前面的行,因为后面的行还没有放置
if(state[i] == col || abs(row - i) == abs(col - state[i]))
return false;
return true;
}
};
算法3:(算法2的非递归版)
class Solution {
private:
vector<vector<string> > res;
public:
vector<vector<string> > solveNQueens(int n) {
vector<int> state(n, -1);
for(int row = 0, col; ;)
{
for(col = state[row] + 1; col < n; col++)//从上一次放置的位置后面开始放置
{
if(isValid(state, row, col))
{
state[row] = col;
if(row == n-1)//找到了一个解,继续试探下一列
{
vector<string>tmpres(n, string(n,'.'));
for(int i = 0; i < n; i++)
tmpres[i][state[i]] = 'Q';
res.push_back(tmpres);
}
else {row++; break;}//当前状态合法,去放置下一行的皇后
}
}
if(col == n)//当前行的所有位置都尝试过,回溯到上一行
{
if(row == 0)break;//所有状态尝试完毕,退出
state[row] = -1;//回溯前清除当前行的状态
row--;
}
}
return res;
}
//判断在row行col列位置放一个皇后,是否是合法的状态
//已经保证了每行一个皇后,只需要判断列是否合法以及对角线是否合法。
bool isValid(vector<int> &state, int row, int col)
{
for(int i = 0; i < row; i++)//只需要判断row前面的行,因为后面的行还没有放置
if(state[i] == col || abs(row - i) == abs(col - state[i]))
return false;
return true;
}
};
算法4(解释在后面)这应该是最高效的算法了
class Solution {
private:
vector<vector<string> > res;
int upperlim;
public:
vector<vector<string> > solveNQueens(int n) {
upperlim = (1 << n) - 1;//低n位全部置1
vector<string> cur(n, string(n, '.'));
helper(0,0,0,cur,0);
return res;
}
void helper(const int row, const int ld, const int rd, vector<string>&cur, const int index)
{
int pos, p;
if ( row != upperlim )
{
pos = upperlim & (~(row | ld | rd ));//pos中二进制为1的位,表示可以在当前行的对应列放皇后
//和upperlim与运算,主要是ld在上一层是通过左移位得到的,它的高位可能有无效的1存在,这样会清除ld高位无效的1
while ( pos )
{
p = pos & (~pos + 1);//获取pos最右边的1,例如pos = 010110,则p = 000010
pos = pos - p;//pos最右边的1清0
setQueen(cur, index, p, 'Q');//在当前行,p中1对应的列放置皇后
helper(row | p, (ld | p) << 1, (rd | p) >> 1, cur, index+1);//设置下一行
setQueen(cur, index, p, '.');
}
}
else//找到一个解
res.push_back(cur);
}
//第row行,第loc1(p)列的位置放置一个queen或者清空queen,loc1(p)表示p中二进制1的位置
void setQueen(vector<string>&cur, const int row, int p, char val)
{
int col = 0;
while(!(p & 1))
{
p >>= 1;
col++;
}
cur[row][col] = val;
}
};
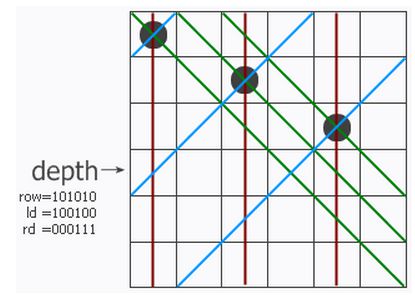
这个算法主要参考博客N皇后问题的两个最高效的算法,主要看helper函数,参数row、ld、rd分别表示在列和两个对角线方向的限制条件下,当前行的哪些地方不能放置皇后。如下图
前三行放置了皇后,他们对第3行(行从0开始)的影响如下: 本文地址
(1)列限制条件下,第3行的0、2、4列(紫色线和第3行的交点)不能放皇后,因此row = 101010
(2)左对角线限制条件下,第3行的0、3列(蓝色线和第3行的交点)不能放皇后,因此ld = 100100
(3)右对角线限制条件下,第3行的3、4、5列(绿色线和第3行的交点)不能放皇后,因此rd = 000111
~(row | ld | rd) = 010000,即第三行只有第1列能放置皇后。
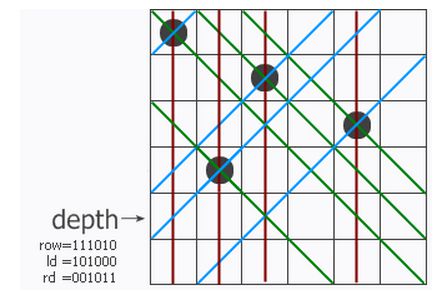
在3行1列这个位置放上皇后,row,ld,rd对下一行的影响为:
row的第一位置1,变为111010
ld的第一位置1,并且向左移1位(因为左对角线对行的影响是依次向左倾斜的),变为101000
rd的第一位置1,并且向右移1位(因为右对角线对行的影响是依次向右倾斜的),变为001011
第4行状态如下图
Follow up for N-Queens problem.
Now, instead outputting board configurations, return the total number of distinct solutions.

这一题就是上一题的简化版了,我们只针对上面的算法2来求解这一题
class Solution {
private:
int res;
public:
int totalNQueens(int n) {
vector<int> state(n, -1);
res = 0;
helper(state, 0);
return res;
}
void helper(vector<int> &state, int row)
{//放置第row行的皇后
int n = state.size();
if(row == n)
{
res++;
return;
}
for(int col = 0; col < n; col++)
if(isValid(state, row, col))
{
state[row] = col;
helper(state, row+1);
state[row] = -1;;
}
}
//判断在row行col列位置放一个皇后,是否是合法的状态
//已经保证了每行一个皇后,只需要判断列是否合法以及对角线是否合法。
bool isValid(vector<int> &state, int row, int col)
{
for(int i = 0; i < row; i++)//只需要判断row前面的行,因为后面的行还没有放置
if(state[i] == col || abs(row - i) == abs(col - state[i]))
return false;
return true;
}
};
【版权声明】转载请注明出处:http://www.cnblogs.com/TenosDoIt/p/3801621.html