1.目标
2.理论
2.1 待拟合公式
$$ f(x)=k·x+b $$,
其中,$ k $, $ b $ 为需要求的参数。
2.2 思路
给定数据集$ D=\{(x_1, y_1),(x_2, y_2),...,(x_n,y_n)\} $,找出$ f(x) $,使得$ f(x_i)=k·x_i+b $尽可能接近 $ y_i $。
2.3 误差计算
使用均方差来计算误差(当然也可以使用其他的)
$$ Loss = \sum_{i=1}^{n}{(f(x_i)-y_i)^2} $$
2.4 反向传播
自己推推就出来了:)(损失函数分别对$k$和$b$求偏导再令其等于0)
3.实现
3.0 环境
python == 3.6
torch == 1.43.1 必要的包
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt # 画图必备3.2 创造数据并预览
x_train = np.array([[3.3],[4.4],[5.5],[6.6],[6.69],[4.4],[9.8],[6.12],[7.7],[2.67],[7.42],[10.91],[5.13],[7.97],[3.1]], dtype=np.float32)
y_train = np.array([[1.7],[2.76],[2.09],[3.19],[1.694],[1.573],[3.366],[2.596],[2.53],[1.221],[2.827],[3.465],[1.65],[2.904],[1.3]], dtype=np.float32)
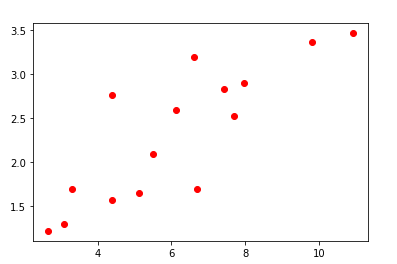
plt.plot(x_train, y_train, 'ro')
plt.show()
# 将numpy对象转换为torch对象
x_train = torch.from_numpy(x_train)
y_train = torch.from_numpy(y_train)3.3 构造模型并创建对象
class LinearRegression(nn.Module):
def __init__(self):
super(LinearRegression, self).__init__()
self.linear = nn.Linear(1,1) # 因为y和x是一对一的关系
def forward(self, x):
out = self.linear(x)
return out
model = LinearRegression()3.4 检查是否有可用的GPU
如果有就将模型和数据放入GPU中训练
if torch.cuda.is_available():
model = model.cuda()
x_train = x_train.cuda()
y_train = y_train.cuda()3.5 创建优化器
# 这是均方误差
criterion = nn.MSELoss()
# 优化器使用随机梯度下降,学习率为0.001
optimizer = optim.SGD(model.parameters(), lr=1e-3)3.6 进行训练
epoch = 0
while True:
out = model(x_train)
loss = criterion(out, y_train) # 损失计算
optimizer.zero_grad() # 梯度清零
loss.backward() # 反向传播
loss_value = loss.data.cpu().numpy() # 获取损失的值
optimizer.step() # 更新参数
# 每100次迭代输出一次损失
if (epoch+1)%100==0:
print('Epoch{}, loss:{:.6f}'.format(epoch+1, loss_value))
epoch += 1
# if loss_value < 1e-3:
if epoch >= 1000: # 1000次迭代后退出
break3.7 验证训练结果
model.eval() # 模型转换为验证模式
predict = model(x_train)
predict = predict.data.cpu().numpy() # 获取预测的值
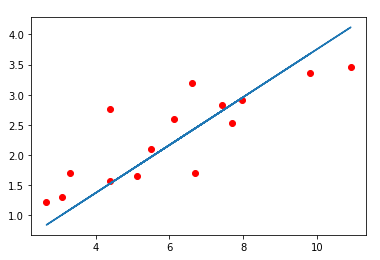
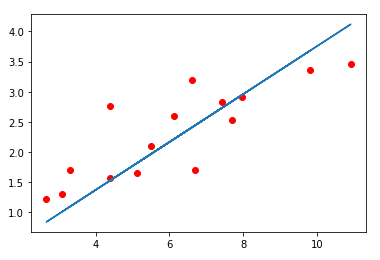
# 'o'代表画点, 'r'代表红色, '-'代表画直线
plt.plot(x_train.cpu().numpy(), y_train.cpu().numpy(), 'ro')
plt.plot(x_train.cpu().numpy(), predict, '-')
plt.show()