NEKO's Maze Game - Codeforces 题解

NEKO#ΦωΦ has just got a new maze game on her PC!

The game's main puzzle is a maze, in the forms of a 2×n2×n rectangle grid. NEKO's task is to lead a Nekomimi girl from cell (1,1)(1,1) to the gate at (2,n)(2,n) and escape the maze. The girl can only move between cells sharing a common side.

However, at some moments during the game, some cells may change their state: either from normal ground to lava (which forbids movement into that cell), or vice versa (which makes that cell passable again). Initially all cells are of the ground type.

After hours of streaming, NEKO finally figured out there are only qq such moments: the ii-th moment toggles the state of cell (ri,ci)(ri,ci) (either from ground to lava or vice versa).

Knowing this, NEKO wonders, after each of the qq moments, whether it is still possible to move from cell (1,1)(1,1) to cell (2,n)(2,n) without going through any lava cells.

Although NEKO is a great streamer and gamer, she still can't get through quizzes and problems requiring large amount of Brain Power. Can you help her?

Input

The first line contains integers nn, qq (2≤n≤1052≤n≤105, 1≤q≤1051≤q≤105).

The ii-th of qq following lines contains two integers riri, cici (1≤ri≤21≤ri≤2, 1≤ci≤n1≤ci≤n), denoting the coordinates of the cell to be flipped at the ii-th moment.

It is guaranteed that cells (1,1)(1,1) and (2,n)(2,n) never appear in the query list.

Output

For each moment, if it is possible to travel from cell (1,1)(1,1) to cell (2,n)(2,n), print "Yes", otherwise print "No". There should be exactly qq answers, one after every update.

You can print the words in any case (either lowercase, uppercase or mixed).

Example

Input

5 5
2 3
1 4
2 4
2 3
1 4

Output

Yes
No
No
No
Yes

Note

We'll crack down the example test here:

• After the first query, the girl still able to reach the goal. One of the shortest path ways should be: (1,1)→(1,2)→(1,3)→(1,4)→(1,5)→(2,5)(1,1)→(1,2)→(1,3)→(1,4)→(1,5)→(2,5).
• After the second query, it's impossible to move to the goal, since the farthest cell she could reach is (1,3)(1,3).
• After the fourth query, the (2,3)(2,3) is not blocked, but now all the 44-th column is blocked, so she still can't reach the goal.
• After the fifth query, the column barrier has been lifted, thus she can go to the final goal again.

题意

2*n的迷宫，从（1，1）出发到（2，n），初始时全部的都是地面，每次询问会把一个地面给变成熔浆，熔浆变成地面，熔浆不能通过，问是否可以走到。

emmm...这道题并没有涉及到什么算法,暴力都会O(n*q),就是减一下复杂度,O(q),其实思路与代码都很简单，看一下应该就会啦。

题解

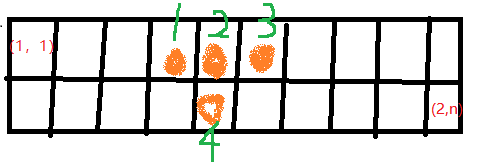
通过读题我们可以知道，在两列的方格中，如果岩浆板块如下图三种情况所示，则会阻碍(2,n)到(1,1)

为了方便，我把图横过来了，上面的4->1  4->2  4->3 三种组合都会阻碍（2，n）到（1，1）。

方法：我们可以用一个变量block存储有多少种阻碍，一个方格每变化一次，就根据它对面三个格子的情况加或减block，加减完判断block是否>0即可。

代码：

 1 #include 
 2 #include 
 3 #include 
 4 using namespace std;
 5 const int maxn=1e5+3;
 6 int block,n,q,x,y;
 7 bool G[3][maxn];
 8 int main(){
 9 //    freopen("1.in","r",stdin);
10     scanf("%d%d",&n,&q);
11     for(int i=1;i<=q;++i){
12         scanf("%d%d",&x,&y);
13         if(G[x][y]==0) G[x][y]=1;else G[x][y]=0;  //0代表无岩浆，1代表有岩浆 
14         if(G[2][n]==1){printf("No\n");continue;} //目的地有岩浆，且目的地与起点不重合，直接No  
15         if(G[x][y]==0){    //如果（x，y）由岩浆改为地面 
16             if(y+1<=n&&G[3-x][y+1]==1)block--;//小技巧,x==1则3-x=2,x==2则3-x=1,实现1<->2转换 
17             if(G[3-x][y]==1)block--;
18             if(y-1>=1&&G[3-x][y-1]==1)block--;
19         }else{            //（x,y）由地面改为岩浆 
20             if(G[3-x][y+1]==1)block++;
21             if(G[3-x][y]==1)block++;
22             if(G[3-x][y-1]==1)block++;
23         }        //block中每加的一个1都对应着唯一的两个坐标组合， 所以不会重复加减的 
24         if(block>0)printf("No\n");
25         else printf("Yes\n");
26     }
27     return 0;
28 }

 2020-04-04 22:22:02