显著性图谱的评价
近来也是做学位论文,其中有一张是对比了当前比较多的图像显著性方法,很多显著性算法都或者给出源码,或者给出可执行程序,或者是提供已分割的结果。
在有以上内容后,如何进行显著性的结果进行评价呢?我看到很多precision-recall曲线图,我以为很多作者都会给出评价的源码,然而实际并没有,虽然评价代码也很容易可以通过matlab编程得到,但无论怎样,还是有点麻烦的,起码我评价9个显著性算法,它得在我电脑上跑将近半天多(也是我偷懒没有优化吧)
对比的方法有:
| 算法名称 | 参考文献 | 实现代码 |
|---|---|---|
| 谱残差(SR) | Hou[40] | 作者提供的Matlab代码 |
| 频率调谐(FT) | Achanta[26] | 作者提供的Matlab代码 |
| 视觉注意(LC) | Zhai[25] | 作者提供的可执行代码 |
| 基于直方图的对比度(HC) | Cheng[31] | 作者提供的可执行代码 |
| 基于区域的对比度(RC) | Cheng[31] | 作者提供的可执行代码 |
| 分层显著性检测(HSD) | Yan[47] | 作者提供的可执行代码 |
| 图的流形排序(GBMR) | Yang[49] | 作者提供的Matlab代码 |
| 全局线索(GC) | Cheng[60] | 作者提供的可执行代码 |
| 稠密稀疏重建(DSR) | Li[52] | 作者提供的可执行代码 |
首先,先看看precision和recall的计算方法:
假设 $Result$ 表示实际分割结果的前景像素点集合,$GT$ 表示该图像真值(Ground Truth)的前景像素值,则precision和recall的计算如下:
$$ precision = \frac{Result\cap{GT}}{Result} $$
$$ recall= \frac{Result\cap{GT}}{GT} $$
$$ F_{\beta} = \frac{(1+(\beta)^{2})\times{precision\times{recall}}}{(\beta)^{2}precision+recall}$$
做过显著性的应该都知道,显著性图是一个从0~255的灰度图,并没有指定哪些是前景,哪些是背景,那么是如何评价的呢?
对于显著性图谱的评测,有种方法叫做固定阈值法,即使阈值从0~255变化,得到每一个阈值对应的precision和recall,遂有了曲线图,其中最高点即为该算法的最佳阈值点。
如下,即是对比图:
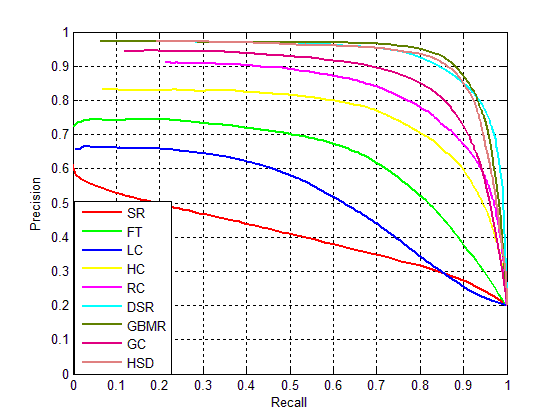
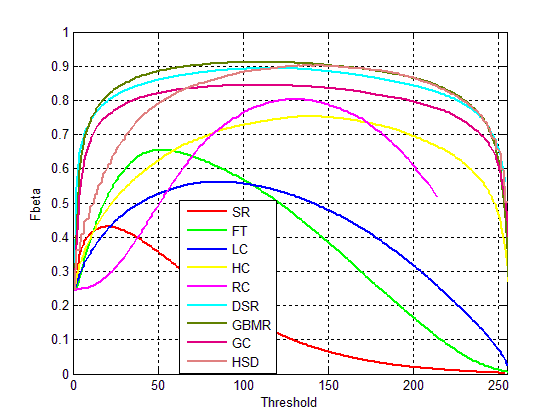
附上我自己写的比较低效率的评测代码:
代码1,计算实验所需的数据,并保存:
clc;
clear all;
srcDir = './Saliency/';
gtFiles = dir([srcDir '*.bmp']);
numFile = length(gtFiles);
maxPixel = 255;
step = 1;
preMatrix = zeros([1 maxPixel/step+1]);
recMatrix = zeros([1 maxPixel/step+1]);
extNames = {'SR', 'FT', 'LC', 'HC', 'RC', 'DSR', 'GBMR', 'GC', 'HSD'};
preMatrixes = zeros([9 maxPixel/step+1]);
recMatrixes = zeros([9 maxPixel/step+1]);
for k=1:9
fprintf('class: %d ...\n',k);
for i=0:maxPixel/step
precision = 0;
recall = 0;
fprintf('%d \t',i);
for j=1:numFile
[path name ext] = fileparts(gtFiles(j).name);
salFilePath = [srcDir name '_' char(extNames(k)) '.png'];
gtLogical = logical(rgb2gray(imread([srcDir gtFiles(j).name])));
salFile = imread(salFilePath);
salFile(find(salFile >= i*step))=255;
salFile(find(salFile < i*step))=0;
salLogical = logical(salFile);
gtNum = length(find(gtLogical==1));
salNum = length(find(salLogical==1));
interNum = length(find((gtLogical & salLogical)==1));
curPre = interNum/salNum;
curRec = interNum/gtNum;
precision = precision + curPre;
recall = recall + curRec;
end
precision = precision/numFile;
recall = recall/numFile;
preMatrix(1,i+1) = precision;
recMatrix(1,i+1) = recall;
end
fprintf('\n');
preMatrixes(k,:) = preMatrix;
recMatrixes(k,:) = recMatrix;
end
save savePreName 'preMatrixes';
save saveRecName 'recMatrixes'代码2,利用实验数据绘制对比数据图:
clc;
clear all;
load savePreName.mat;
load saveRecName.mat;
extNames = {'SR', 'FT', 'LC', 'HC', 'RC', 'DSR', 'GBMR', 'GC', 'HSD'};
lineColors = zeros([9 3]);
lineColors(1,:) = [1 0 0];
lineColors(2,:) = [0 1 0];
lineColors(3,:) = [0 0 1];
lineColors(4,:) = [1 1 0];
lineColors(5,:) = [1 0 1];
lineColors(6,:) = [0 1 1];
lineColors(7,:) = [0.4 0.5 0];
lineColors(8,:) = [1 0 0.5];
lineColors(9,:) = [1 0.5 0.5];
figure(1);
for k=1:9
recall = recMatrixes(k,:);
precision = preMatrixes(k,:);
plot(recall, precision, 'Color',lineColors(k,:), 'linewidth', 2);
hold on;
end
hold off;
xlabel('Recall');
ylabel('Precision');
legend('SR', 'FT', 'LC', 'HC', 'RC', 'DSR', 'GBMR', 'GC', 'HSD');
grid on;
axis([0 1 0 1]);
Fbeta = zeros([9 256]);
for k=1:9
for i=0:255
rec = recMatrixes(k,i+1);
pre = preMatrixes(k,i+1);
Fbeta(k,i+1) = (1+0.3)*pre*rec/(0.3*pre+rec);
end
end
figure(2);
for k=1:9
plot(Fbeta(k,:),'Color',lineColors(k,:), 'linewidth', 2);
hold on;
end
hold off;
xlabel('Threshold');
ylabel('Fbeta');
legend('SR', 'FT', 'LC', 'HC', 'RC', 'DSR', 'GBMR', 'GC', 'HSD');
grid on;
axis([0 255 0 1]);