新冠病毒带走了用游戏创造「生命」的数学家

只愿这场灾难早日结束。
两周前,世界著名数学家、普林斯顿大学的约翰·康威(John Horton Conway)教授因为感染新冠肺炎不幸去世,享年83岁。
康威1937年出生在英国利物浦,在博弈论、群论和几何学领域都做出过突出的贡献。但是他最为人熟知的作品,却是一个被称为《生命游戏》的计算机程序。
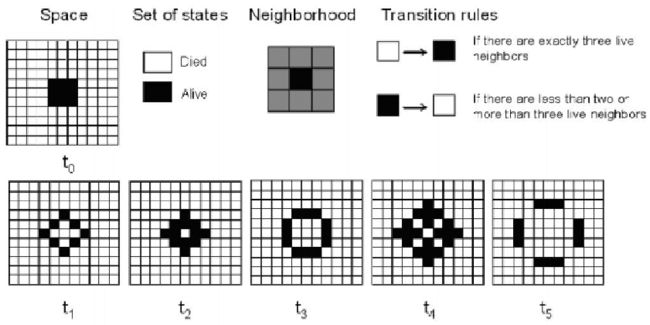
《生命游戏》叫做“游戏”,其实绝大部分时间都是计算机在无人干预的情况下自己进行运算。程序在一个二维的网格上运行,每个格子被称为一个“细胞”。康威设置了一套规则定义每个“细胞”的生死:
如果一个活细胞相邻超过三个细胞,或者少于两个细胞,这个细胞就会死。如果一个活细胞周围刚好有2-3个细胞,这个细胞就会保持存活。如果一个死细胞周围有3个活细胞,这个死细胞就会活过来。
在康威规则下一个图形演变的过程
当细胞的生死状态发生改变时,周围细胞的生死状态也可能会跟着发生变化,形成链式反应,直到所有细胞都变成一个稳定的状态。玩家可以自己先画好一个初始图像,让程序运行,然后看这些“细胞”在规则下逐渐演化的过程。比如最著名的图案“橡子”,形状非常简单,但是却会在《生命游戏》的网格上不断生长壮大,就像种子变成大树一样。
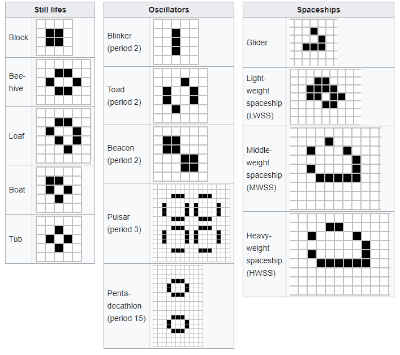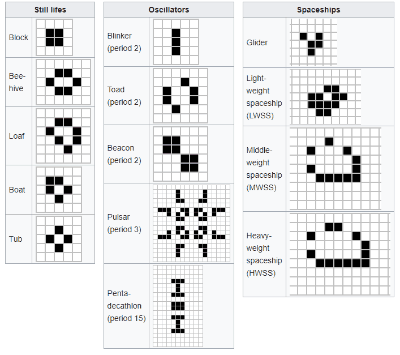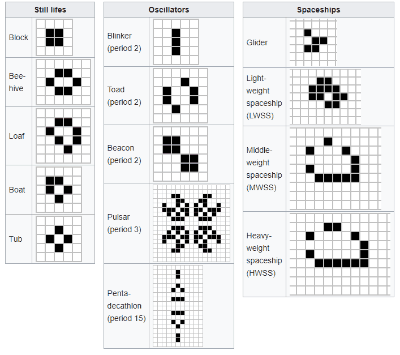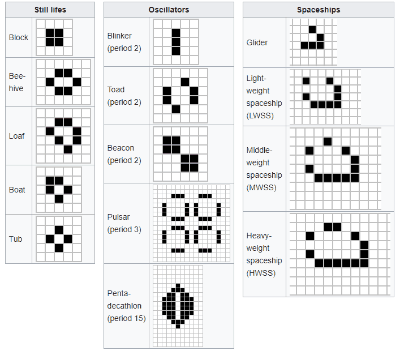
在《生命游戏》演化的过程中,会出现几种非常典型的基本图案,比如蜂巢、面包、蟾蜍、宇宙飞船等等。
维基给出的一些基本图形范例
巧妙利用这些基本图案的行为特征,就能设计生成更加复杂的图案,比如会不停发射出子弹的“机关枪”:
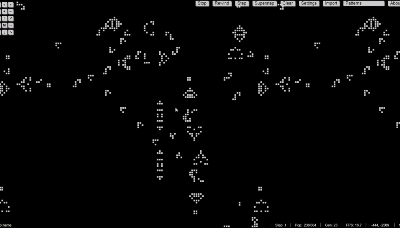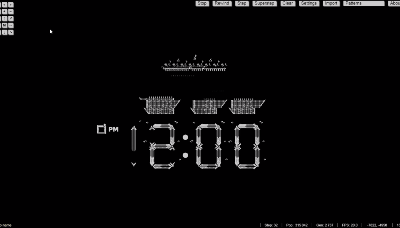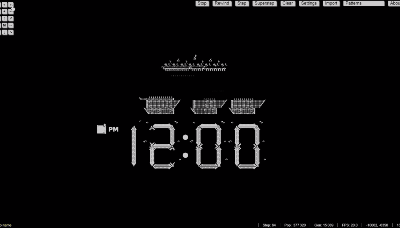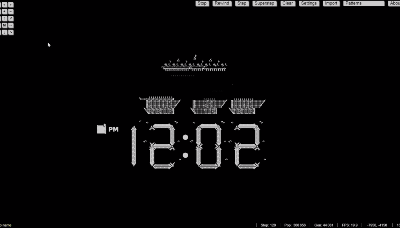
能够生产出复杂飞船的流水线:
甚至还能组合出复杂的逻辑电路,实现特定的功能,比如手表:
可能有人以为这种像生命一样不断进化,从细胞变成个体,再形成社群的过程,就是《生命游戏》名字的来历。但是如果从康威的解释来看,这个名字更多指的是《生命游戏》的规则和DNA碱基配对编码规则一样,是一套简单但有效的信息解码机制。
《生命游戏》诞生于1970年代,康威回忆,这个游戏最初的启发,是冯·诺伊曼对人类移民宇宙的设想。冯·诺伊曼提出的方案是:先派遣一些机器人到火星上,用火星上的氧化铁制造铁和氧气。氧气用来改造大气层,铁用来制造新的机器。
反对这个设想的人认为,想要制造机器,必须先生产更复杂的机器。但是冯·诺伊曼觉得,一个机器只要能生产出简单的零件,就能用这些零件组合成复制自己。
康威认为冯·诺伊曼的想法在数学上是可行的,所以他仿照DNA碱基配对编码的原理创作了《生命游戏》作为演示。在康威看来,只要《生命游戏》能够把特定信息转化成一套运算和生产过程,就像DNA解码生产复杂的蛋白质那样,就算是演示出了冯·诺伊曼设想的正确性。
玩家最终在《生命游戏》中创造了《生命游戏》,利用无数小细胞组成的巨大化“轻型宇宙飞船”
当然,为了这种演示能够有更好的效果,康威还是对规则进行了比较细致的调整,直到最后成为《生命游戏》中那种简洁又有效的样子。康威觉得,这个规则或许还有优化的空间,但是从数学的角度,已经没有太大研究和改进的价值。
整个工程花费了康威大概一年半的闲暇时间。对于他来说,这不过就是一个兴趣使然的消遣而已。
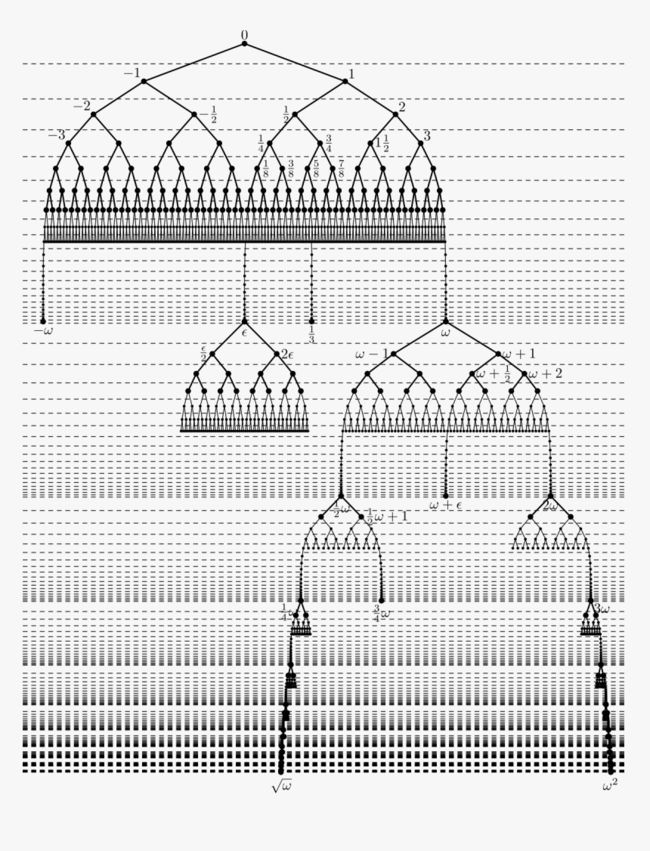
在同期,他还在忙于他的“超现实数”理论。“超现实数”将博弈的整个过程抽象成了一个数集,并且这个数集还能进行加减乘除的运算,是最具有想象力的数学理论之一。著名计算机科学家高德纳的科幻小说《研究之美》(英文原名:Surreal Numbers,即“超现实数”),其实在某些层面上就是一本解读超现实数概念的数学科普读物。
从这个角度,很好理解为什么康威在有一段时间里面不太喜欢谈论《生命游戏》。康威曾说,这个作品经过《科学美国》杂志上一篇科普专栏的介绍而为大众所熟知,读者回信打破了《科学美国》杂志的历史记录。在此之后,不管康威参加什么活动,出席什么会议,甚至给学生上课,都一定会有人提到《生命游戏》,掩盖了他其他工作的价值。
不过他这么说,可能也只是单纯对别人老是提到《生命游戏》而感到厌烦。毕竟康威自己是一个挺喜欢胡闹的人。康威说,自己差不多有25年时间,都活得像是25岁:只要自己感兴趣的东西,就会去研究研究,鼓捣鼓捣。他生平最得意的独门绝技,是一套高超的卷舌技巧,是自己大学学院历史上第一个能够完成所有卷舌动作的人。
除了《生命游戏》,康威还发明过《豆芽》《哲人足球》这些看似简单,却包含着高深的数学逻辑的对弈游戏。这些工作一度被其他数学家批评为“玩闹”(trivial),但是康威却乐在其中。
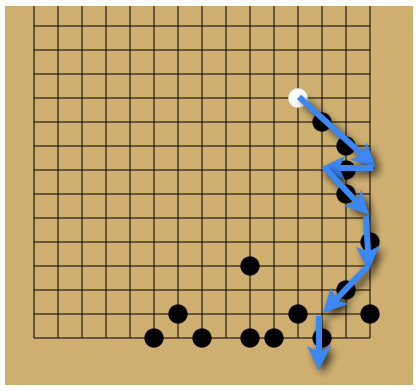
哲人足球是一个在围棋棋盘上进行的拓扑游戏
好玩的是,在康威设计《生命游戏》的时候,普林斯顿甚至还没有可以编程的计算机。所以《生命游戏》是等前期数学工作都做完了,等到有了计算机,才把《生命游戏》编写成程序跑起来。
尽管康威对《生命游戏》的数学价值很不以为然,但是这部作品对计算机科学却有着十分深远的影响。《生命游戏》是 “元胞自动机”最直观有趣的应用之一,也是了解冯·诺伊曼结构计算机原理的一个非常有效的方式。很多经典的计算机编程相关的题目,都会以《生命游戏》作为案例。
如果将《生命游戏》中细胞的“生”和“死”看作计算机电路中的1和0,就不难理解计算机为什么能够用两种基本状态实现各种复杂的功能。联想到人工智能的巨大潜力,或许康威在《生命游戏》中真的找到了某种未来生命形式的原初形态也说不定。
尽管康威去世时已经83岁,但是他的思路依然清晰,也经常在各种数学节目中出现。他能够继续享受数学带给他的乐趣的时间应该尚有一些日子。他的骤然离去,让人感到悲伤和遗憾。最让人难过的是,而在不久的将来,类似的悲伤或许还会重复上演。
我们始终欢迎喜欢内容创作的小伙伴加入
应聘简历可发邮箱:[email protected]
文章投稿可发邮箱:[email protected]



点击在看,将好文分享给更多人