数据结构--堆的实现
1,堆是什么?
堆的逻辑结构是一颗完全二叉树,但物理结构是顺序表(一维数组)。同时,此处的堆不要与JAVA内存分配中的堆内存混淆。这里讨论的是数据结构中的堆。
参考:计算机中的堆是什么?
2,数组实现堆的优势及特点
由于堆从逻辑上看是一颗完全二叉树,因此可以按照层序遍历的顺序将元素放入一维数组中。注意为了方便,数组的元素存放从索引 1 处开始(不是0)。采用数组来存放就很容易地找到某个结点 i 的双亲结点(i/2),孩子结点(左孩子:2i,右孩子:2i+1)
3,基于数组的堆的实现需要哪些结构?
private T[] heap;//用来存储堆元素的数组 private int lastIndex;//最后一个元素的索引
private static final int DEFAULT_INITIAL_CAPACITY = 25;
首先需要一个一维数组heap来保存堆中的元素;其次,需要lastIndex标记堆中最后一个元素的索引,这样也知道了堆中存放了多少个元素;最后,需要一个final静态变量定义默认构造堆的大小。
4,JAVA中基于一维数组的堆的实现具体代码分析
①创建堆,假设有N个元素,需要将这N个元素构建大顶堆,有两种方法来创建堆。一种是通过add()方法,另一种是通过reheap()方法。现在分别讨论如下:
对于add方法:当要向堆中添加新元素时,调用该方法完成添加元素的操作。那么对这N个元素逐一调用add方法,就可以将这N个元素构造成大顶堆,此时的时间复杂度为O(nlogn)。add方法的代码如下:
public void add(T newEntry) { lastIndex++; if(lastIndex >= heap.length) doubleArray();//若堆空间不足,则堆大小加倍 int newIndex = lastIndex;//从最后一个元素开始逐渐向上与父结点比较 int parentIndex = newIndex / 2; heap[0] = newEntry;//哨兵 while(newEntry.compareTo(heap[parentIndex]) > 0){ heap[newIndex] = heap[parentIndex]; newIndex = parentIndex; parentIndex = newIndex / 2; } heap[newIndex] = newEntry; }
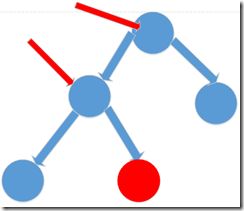
假设树中有n个元素,则完全二叉树高为logn,调用add方法的时间复杂度为O(logn)。向堆中插入新元素的具体操作如下:首先将元素数组的最后一个位置,然后从该位置起向上调整,直至到根结点为止。
如图,当插入新的红色结点时,首先将它放在堆的末尾,然后进行再次堆调整(红色箭头所指)。
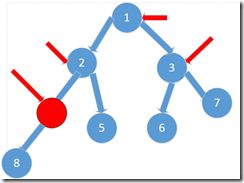
对于使用reheap方法来创建堆:N个元素逻辑上组成一颗完全二叉树,从它的最后一个非叶子结点开始,逐渐向前调整,直至调整到根结点。对于每个被调整的结点,将以该结点为根的子树调整成一个(子)堆。假设有8个元素的数组,将将会从第4个元素起,开始进行堆调整(调用reheap方法),直至调整到第 1 个元素为止。该方法建堆的时间复杂度为O(n)
reheap方法的代码如下:
/* * @Task:将树根为rootIndex的半堆调整为新的堆,半堆:树的左右子树都是堆 * @param rootIndex 以rootIndex为根的子树 */ private void reheap(int rootIndex){ boolean done = false;//标记堆调整是否完成 T orphan = heap[rootIndex]; int largeChildIndex = 2 * rootIndex;//默认左孩子的值较大 //堆调整基于以largeChildIndex为根的子树进行 while(!done && (largeChildIndex <= lastIndex)){ //largeChildIndex 标记rootIndex的左右孩子中较大的孩子 int leftChildIndex = largeChildIndex;//默认左孩子的值较大 int rightChildIndex = leftChildIndex + 1; //右孩子也存在,比较左右孩子 if(rightChildIndex <= lastIndex && (heap[largeChildIndex].compareTo(heap[rightChildIndex] )< 0)) largeChildIndex = rightChildIndex; // System.out.println(heap[largeChildIndex]);//这里有问题。。使用构造函数创建时reheap。。。。。 if(orphan.compareTo(heap[largeChildIndex]) < 0){ heap[rootIndex] = heap[largeChildIndex]; rootIndex = largeChildIndex; largeChildIndex = 2 * rootIndex ;//总是默认左孩子的值较大 } else//以rootIndex为根的子树已经构成堆了 done = true; } heap[rootIndex] = orphan; }
第4个元素就是最后一个非叶子结点。(红色箭头表示需要进行堆调整的结点)
两种建堆方法的比较:
add方法合适于动态建堆,也就是说,来一个元素,调用add方法一次,再来一个元素,再调用add方法……直至构造了一个N个元素的堆。而对于reheap方法,它是先给定了N个元素,这N个元素表示成一颗完全二叉树的形式,然后从树的最后一个非叶子结点开始,依次往前调整,进而构造堆。
add方法的调整与reheap方法的调整是不相同的。add方法的整个调整过程如下:该元素被添加到了数组最后一个位置lastIndex,然后,lastIndex与 (lastIndex / 2) 比较……即它总是与它的双亲结点比较。这一个元素调整完后,再来下一个元素,同样先将它放到数组最后,再与它的双亲比较……调整的方向是自下而上的。
reheap方法的调整过程如下:如上图,第4号结点与它的孩子(第8号结点)比较,进行调整,使之满足堆的定义。再接着是第3号结点与它的两个孩子比较,进行调整。再接着是第2号结点与它的孩子比较(第4,5号结点),若有必要还得与第8号结点比较,……调整的方向是自上而下的。(上面已经提到,即 以从第4号结点开始,对该结点为根的子树进行调整,将该子树调整成一个堆)。
5,堆排序算法的实现
对于一个排序算法而言,首先得有一组可比较的数据拿来给你排序。故假设排序算法需要一个装有待排序数据的一维数组 arr。这里就有两种方法来实现排序:
❶:根据待排序的数据(一维数组 arr)创建一个堆,由于这里可以采用第二种建堆方法(reheap方法),故建堆的时间复杂度为O(n);空间复杂度也为O(n),因为创建的堆本质上是个一维数组,它就是由 n 个待排序数据组成的。
ArrayMaxHeap<Integer> heap = new ArrayMaxHeap<Integer>(arr);
然后,从 heap 中删除元素时,将删除的元素按顺序放回到数组arr中,直至将heap中的元素删除完毕后全部放回到数组arr中后,数组arr就变成了有序的了。(堆的性质保证了每次从堆中删除元素时总是删除堆中最大的元素(即最大堆的堆顶元素))。由于每次从堆中删除元素的时间复杂度为O(logn) ,故整个堆排序的时间复杂度为O(nlogn)、空间复杂度为O(n)。
❷: 第二种堆排序的实现方法如下:
还是根据给定的一维数组arr 通过反复调用reheap方法来创建堆。但是,是在arr上创建堆,而不是新开辟一个数组来创建堆。这样,使得整个排序过程的空间复杂度为O(1)
由于是直接在 数组arr 上创建堆,故堆创建的索引是从0开始,而不是从1开始了。
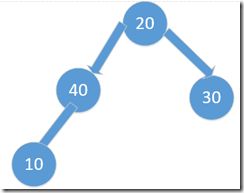
在arr数组上建堆后,arr数组中元素的顺序就是符合堆定义的顺序了(完全二叉树中父结点的值比孩子结点的值要大)且第一个元素为最大元素;因为第一个元素为堆顶元素。因此,可以把 数组arr 中的第一个元素与最后一个元素交换,这样 arr 的前 n-1 个元素就构成了一个半堆(树根的左右子树都是堆称为半堆),这样就可以进行reheap操作将前n-1个元素重新调整成堆。
下图就是一个半堆,根结点20的左右子树都是堆,但整个完全二叉树不是堆。
接着,又将第一个元素与倒数第二个元素交换,剩下的前n-2个元素构成了一个半堆,又进行reheap操作将之调整为堆……反复执行上述步骤即可将arr排序。
由于该方法是直接在arr上建堆并排序的。故空间复杂度为O(1),而每次执行reheap方法的时间复杂度为O(logn),共有n个元素,需要执行n次reheap,故整个堆排序的时间复杂度为O(nlogn),空间复杂度为O(1)。
关于时间复杂度的分析 有个小问题:第一次reheap方法需要调整的半堆有n-1个元素,第二次reheap方法调整的半堆有n-2个元素……,也就是说,每次reheap所需要执行的调整次数是越来越少的。但总的时间复杂度还是O(nlogn)了。
整个堆实现的完整代码下载:堆的实现(可运行)--JAVA代码下载