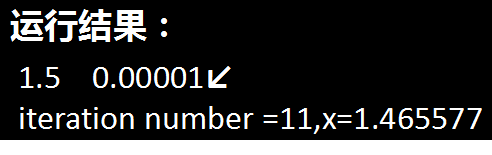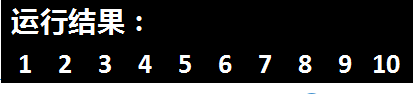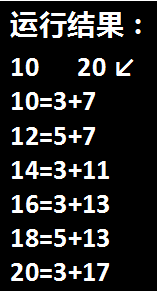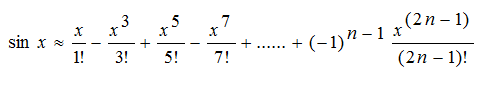《C语言综合应用》课程学习(1)——第1章 程序设计方法
1.1 问题求解
1.问题的分类
计算学科中有许多著名的算法类问题,例如哥尼斯堡七桥问题、梵天塔问题、背包问题、旅行商问题及项目调度优化问题等。
系统类问题广泛存在于工程、科学、经济等领域,例如,卫星导航系统就是典型的系统类问题。
算法类问题和系统类问题的求解过程、思维和方法是有很大区别的。
(1)解决算法类问题需要建立数学模型、设计数据结构、设计算法,利用某种程序设计语言编写程序等几个步骤。
(2)系统类问题求解需要建立业务模型、建立软件模型、开发软件模块,将其组装为软件系统并将其部署到实际环境中运行。
2.算法的定义
是一组有穷的规则,它规定了解决某一特定类型问题的一系列运算。
3.算法的特征
4.程序
程序是算法用某种程序设计语言的具体实现。
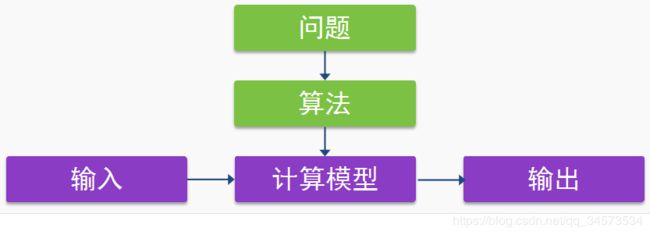
5.问题的求解过程
例:求两个不全为0的非负整数m和n的最大公约数。
1.2 穷举法
1.基本思想
又称枚举法,或暴力法。从问题可能的解的集合中按某种顺序进行逐一枚举和检验,从中找出那些符合要求的候选解作为问题的解。
2.特点
列举所有可能的解(既不能遗漏,也不能重复),检验每个可能的解。
3.典型应用实例
水仙花数、百钱买百鸡、密码学中的暴力破解方法、旅行商中线路计算问题等。
百钱买百鸡问题概述:
一百个铜钱买了一百只鸡,其中公鸡一只5钱、母鸡一只3钱,小鸡一钱3只,问一百只鸡中公鸡、母鸡、小鸡各多少)。
这是一个古典数学问题,设一百只鸡中公鸡、母鸡、小鸡分别为x,y,z,问题化为三元一次方程组:
这里x,y,z为正整数,且z是3的倍数;由于鸡和钱的总数都是100,可以确定x,y,z的取值范围:
1) x的取值范围为1~20
2) y的取值范围为1~33
3) z的取值范围为3~99,步长为3
对于这个问题我们可以用穷举的方法,遍历x,y,z的所有可能组合,最后得到问题的解。
4.使用穷举法需要解决的基本问题
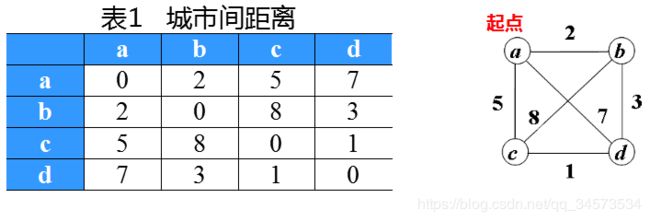
例1:旅行商问题(TSP):旅行家要旅行n个城市然后回到出发城市,任何两个城市之间的距离都是确定的,要求各个城市经历且仅经历一次,并要求所走的路程最短。
#include "stdio.h"
main()
{ int d[4][4]={{0,2,5,7},{2,0,8,3},{5,8,0,1},{7,3,1,0}},sum[6],i,j,smin;
char pat[6][10]={"abcda","abdca","acbda","acdba","adbca","adcba"};
sum[0]=d[0][1]+d[1][2]+d[2][3]+d[3][0];
sum[1]=d[0][1]+d[1][3]+d[3][2]+d[2][0];
sum[2]=d[0][2]+d[2][1]+d[1][3]+d[3][0];
sum[3]=d[0][2]+d[2][3]+d[3][1]+d[1][0];
sum[4]=d[0][3]+d[3][1]+d[1][2]+d[2][0];
sum[5]=d[0][3]+d[3][2]+d[2][1]+d[1][0];
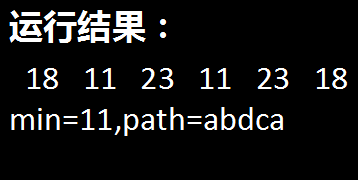
for(i=0; i<6; i++)
printf("%5d",sum[i]);
smin=0;
for(i=1;i<6;i++)
if(sum[smin]>sum[i]) smin=i;
printf("\nmin=%d,path=%s\n",sum[smin],pat[smin]);
}5.穷举法小结
6.可行解与最优解
1.3 贪心法
1.基本思想
从问题的初始状态出发,通过若干次的贪心选择而得出最优解或较优解的一种解题方法。
2.贪心策略
贪心的策略根据当前已有的信息就做出选择,而且一旦做出了选择,不管将来有什么结果,这个选择就不会改变。
3.贪心解题步骤
例2:利用贪心法求解TSP
例2:旅行商问题(TSP):旅行家要旅行n个城市然后回到出发城市,任何两个城市之间的距离都是确定的,要求各个城市经历且仅经历一次,并要求所走的路程最短。
代码说明:
s[ ]:存放最短路径中的城市代码;
i:代表寻找到的最短路径中的城市个数;
j:代表当前路径最短的城市名称的代号,例如0代表a,1代表b,2代表c,3代表d;
k:代表正在求解的城市名称的代号,例如0代表a,1代表b,2代表c,3代表d;
l:用来表示已经找到的最短路径的第几个城市。
4.优点
因为省去了为寻找解而穷尽所有可能所必须耗费的大量时间,因此算法效率高。
5.缺点
不能保证求得的最后解是最佳的;只能求满足某些约束条件的可行解的范围。
1.4 迭代和递推
1.基本思想
迭代法也称“辗转法”,是一种不断用变量的旧值递推出新值的解决问题的方法。
2.特点
把一个复杂问题的求解过程转化为相对简单的迭代算式,然后重复执行这个简单的算式,直到得到最终解。
3.分类
精确迭代和近似迭代。
说明:
- 迭代是指重复执行一组操作。每次执行这些操作时,都会有一个或一组变量的值发生变化,而且这种变化一直朝着问题的答案方向迈进。当得到答案时,迭代过程结束。
- 迭代法又分为精确迭代和近似迭代。“二分法”和“牛顿迭代法”属于近似迭代法。
- 解方程迭代法和牛顿迭代法都是通过迭代公式迭代求解,二分法是另一种方式的迭代。
由于迭代公式收敛性的判断不是一个简单的问题,需要计算数学等方面的知识,程序中一般采用控制迭代次数的方法。如果某迭代公式在M次迭代之内使|xn+1-xn|<ε成立,则认为该迭代收敛,否则认为发散。
float f (float x)
{ return x*x*x*x-5*x*x+x+2; }
float duifen(float a,float b,float eps)
{ float c,z;
while (b-a>=eps)
{ c=(a+b)/2;
if (f(c)==0) return c;
else if (f(a)*f(c)<0) b=c;
else a=c;
}
return c;
}
#include "stdio.h"
#include "math.h"
main ( )
{ float duifen(float a,float b,float eps);
float f (float x);
float a,b,r,eps;
scanf("%f%f",&a,&b);
scanf("%f",&eps);
r=duifen(a,b,eps);
printf("%f\n",r);
}迭代不一定非得与精度控制相联系,斐波纳契数列就是这种迭代的典型代表。
#include
#include "math.h"
main()
{ long f1,f2,f3;
int i,n;
scanf("%d",&n);
f1=1; f2=1;
printf("%10ld%10ld",f1,f2);
for(i=3;i<=n;i++)
{ f3=f1+f2;
printf("%10ld",f3);
if(i%5==0) printf("\n");
f1=f2;
f2=f3;
}
} 迭代法小结
(1)迭代一般需要有相应的迭代公式,二分法是通过隔根区间两端点的函数值是否同符号来不断缩小隔根区间。
(2)迭代法都有一个或多个迭代变量,迭代的次数与这些迭代变量有关,能否找到和使用合适的迭代变量是程序设计的关键问题之一。
这几种迭代法都通过判断方程的两个近似根之间的差的绝对值是否小于10-n来决定是否终止迭代过程。斐波纳契数列求解也有迭代公式:f(n)=f(n-1)+f(n-2),但这种类型的迭代和某些累加(如S=S+T)、累积等迭代一样,并不是通过判断某个差的绝对值是否小于10-n来终止迭代过程的。
例1-3和例1-4中的迭代变量是x,二分法中迭代变量是隔根区间的左右边界a和b的中点c,求斐波纳契数列时迭代变量是f3。
1.5 递归法
1.定义
递归是一种直接或间接地调用自身的算法。
2.递归的本质
递归把一个大型、复杂的问题层层转化为一个与原问题相似、但规模较小的问题来求解。递归的能力在于用有限的语句来定义对象的无限集合。
3.递归的视觉形式:德罗斯特效应
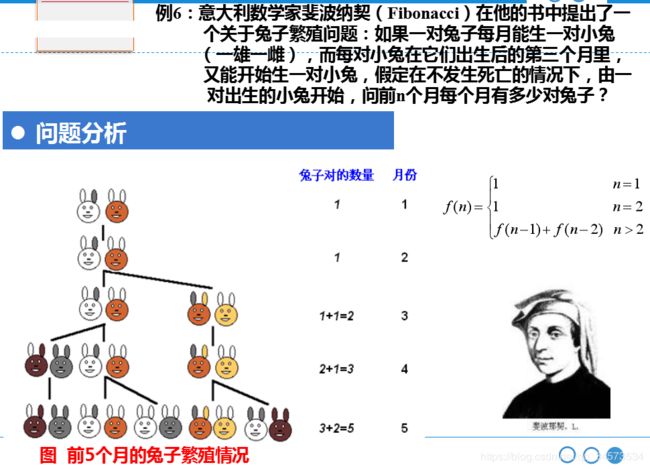
斐波那契数列还可以使用递归的方法来求解。
4.递归的两个基本要素
例7:递归法求解斐波那契数列问题
5.递归的执行过程
递推
把规模为n的问题的求解推到比原问题的规模较小的问题求解,且必须要有终止递归的情况。
回归
当获得最简单情况的解后,逐级返回,依次得到较大规模的解。
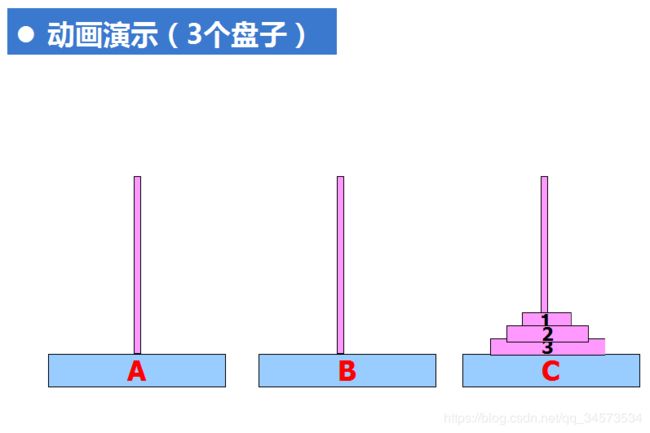
例8:梵天塔问题
古代有一个梵天塔,塔内有3个座A、B、C,开始时A座上有64个盘子,盘子大小不等,大的在下,小的在上。有一个老和尚想把这64个盘子从A盘移到C座。
规则1:每次只允许移动一个盘子;
规则2:在移动过程中在3个座上都始终大盘在下,小盘在上。
在移动过程中可以利用 B座。
void HN(int n,char a,char b,char c)
{ if(n==1)
printf("from %c to %c\n",a,c);
else
{ HN(n-1,a,c,b);
printf("from %c to %c\n",a,c);
HN(n-1,b,a,c);
}
}
#include
main()
{ void HN(int n,char a,char b,char c);
int m;
printf("Please input the number of plate:\n");
scanf("%d",&m);
printf("%d plate moving steps are as follows:\n",m);
HN(m,'A','B','C');
} 5.优点
结构清晰、可读性强、容易证明算法的正确性。
6.缺点
运行效率低。
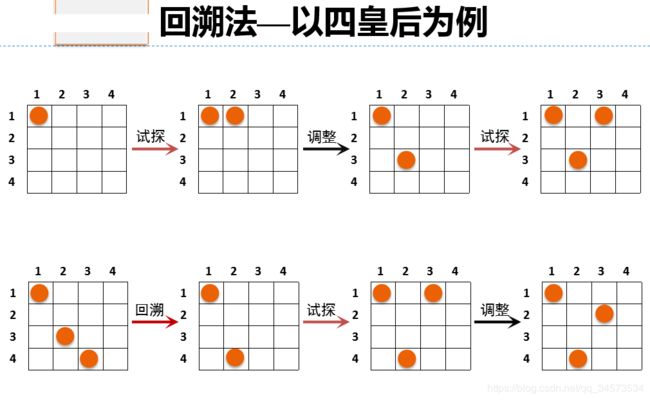
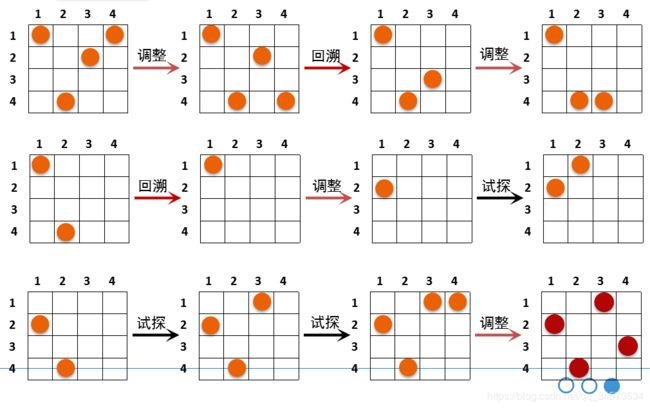
1.6 回溯法
1.定义
回溯法也称为试探法,该方法首先放弃关于问题规模大小的限制,并将问题的候选解按某一顺序逐一枚举和试验。当发现当前候选解不可能是解时,就选择下一个候选解;倘若当前候选解除了还不满足问题规模要求外,满足所有其它要求时,继续扩大当前候选解的规模,并继续试探。如果当前候选解满足包括问题规模在内的所有要求时,该候选解就是问题的一个解。
2.典型应用实例
老鼠走迷宫、八皇后问题
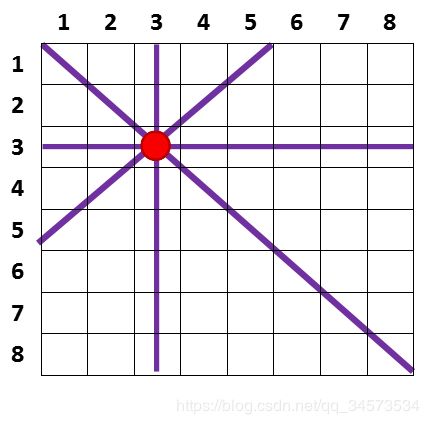
例9:八皇后问题
问题描述:在一个8×8国际象棋棋盘上,有8个皇后,每个皇后占一格;要求皇后间不会出现“相互攻击”的现象,即不能有两个皇后处在同一行、同一列或同一对角线上。问共有多少种不同的方法?
例9:八皇后问题代码:
#include
#define N 8
int chess[N][N] = {0};
int count = 0;
int canput(int row, int col)
{ int i,j;
for(i = 0; i < N; i ++)
{ if(chess[i][col] == 1) return 0;
for(j = 0; j < N; j++)
{ if(chess[row][j]==1) return 0;
if(((i-row)==(j-col)||(i-row)==(col-j))&&chess[i][j]==1) return 0;
}
}
return 1;
}
void print_chess()
{ int i, j;
for(i = 0; i < N; i++)
{
for(j = 0; j < N; j++)
printf("%d ", chess[i][j]);
printf("\n");
}
printf("\n");
}
int put(int row)
{ int j, s;
for(j = 0; j < N; j++)
{ if(canput(row, j))
{ chess[row][j] = 1;
if(row == N-1)
{ count = count +1;
print_chess();
chess[row][j] = 0;
continue;
}
s = put(row+1);
if(s == 0) { chess[row][j] = 0; continue; }
else break;
}
}
if (j==N) return 0;
else return 1;
}
main()
{ int s ;
s = put(0);
printf("the number of put way is %d\n", count);
return 0;
} 1.7 分治法
1.定义
对于一个规模为 n 的问题,将其分解为 k 个规模较小的子问题,这些子问题相互独立且与原问题形式相同,递归的解决这些子问题,然后将各个子问题的解合并,得到原问题的解。
2.基本思想
将一个难以直接解决的大问题,分解成一些规模较小的子问题,以便各个击破,分而治之。然后把各个子问题的解合并起来,得出整个问题的解。
3.分治策略的基本步骤
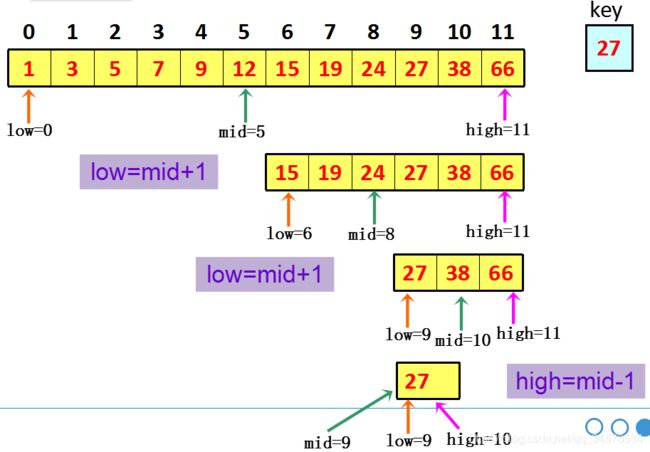
例10:用二分查找法找一个数是否在一个 有序数组中。
#include "stdio.h"
main()
{ int n=12,a[]={1,3,5,7,9,12,15,19,24,27,38,66},key,mid,low,high;
printf("input the number:\n");
scanf("%d",&key);
low=0; high=n-1;
while(low<=high)
{ mid=(low+high)/2;
if(key==a[mid]) { printf("%d\n",mid); break; }
else if(keyhigh) printf("nod found\n");
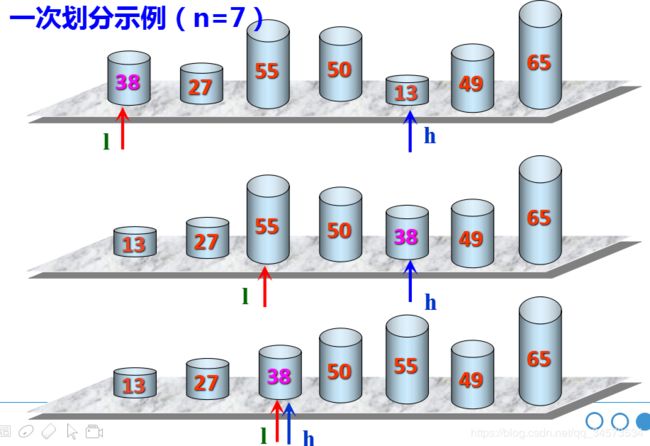
} 例11:利用快速排序法对10个整数进行由小到大的排序。
void quicksort (int a[], int left, int right)
{ int low,high,key;
if(left < right)
{ key =a[left];
low = left;
high = right;
while(low < high)
{ while(low < high && a[high] > key) high--;
a[low] = a[high];
while(low < high && a[low] < key) low++;
a[high] = a[low];
}
a[low] = key;
quicksort(a,left,low-1);
quicksort(a,low+1,right);
}
}
main()
{ int a[10]={5,2,4,7,9,10,8,3,1,6},i;
quicksort(a,0,9);
for(i=0;i<10;i++)
printf("%5d",a[i]);
}1.8 自顶向下与逐步求精
1.面向过程的结构化程序设计方法
结构化程序设计是一种设计程序的技术,它采用自顶向下、逐步求精的方法和单入口和单出口的程序结构。
2.基本思想
将一个复杂问题按照功能进行拆分,并逐层细化到便于理解和描述的程度,最终形成由多个小模块组成的树形结构。
例12:对M至N之间的大偶数验证哥德巴赫猜想
哥德巴赫猜想:一个大的偶数(≥6)可以表示成两个奇素数之和。
#include "stdio.h"
int main()
{ int m,n,i,j,i1,k,a,b;
do
{ scanf("%d%d",&m,&n);
if(m>=6 && m<=n&&m%2==0) break;
} while(1);
for(k=m;k<=n;k+=2)
for(i=3;i<=k-3;i+=2)
{ i1=k-i;
if(prime(i)==1&&prime(i1)==1)
{ printf("%d=%d+%d\n",k,i,i1);
break;
}
}
}
int prime(int n)
{ int i;
for(i=2;i<=n/2;i++)
if (n%i==0) return 0;
return 1;
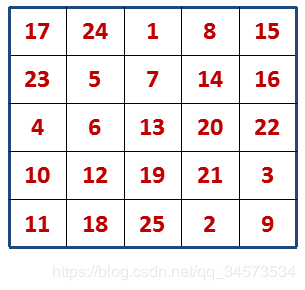
}例13:对奇数 n 输出纵横图。
纵横图:每行、每列及两条对角线的和都相等的方阵。
#include "stdio.h"
#define N 5
main()
{ int a[N][N]={0},i,j,k,i1,j1;
i=0; j=N/2;
for(k=1; k<=N*N; k++)
{ a[i][j]=k; i1=i-1; j1=j+1;
if(i1<0) i1=N-1 ;
if(j1>N-1) j1=0;
if(a[i1][j1]==0) { i=i1; j=j1; }
else i++;
}
for(i=0;i例14:按以下公式求sinx的近似值,x和n由键盘输入。
#include "stdio.h“
#include "math.h”
main()
{ float t,x,s;
int i,j,n;
scanf("%f%d",&x,&n);
for(i=1;i<=n;i++)
{ t=1;
for(j=1;j<=2*i-1;j++)
t=t*x/j;
s=s+pow(-1,i-1)*t;
}
printf("x=%f,s=%f\n",x,s);
}1.9 程序调试的简单方法
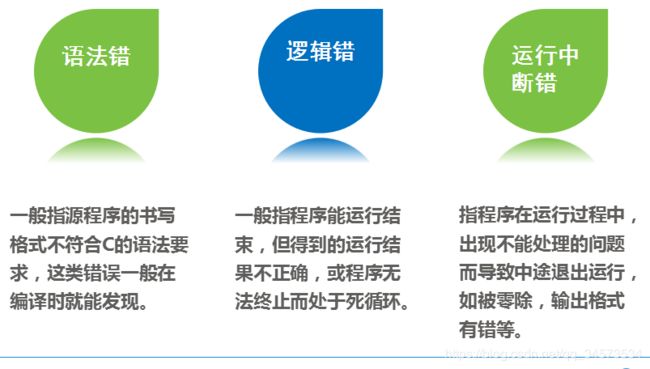
1.错误的种类
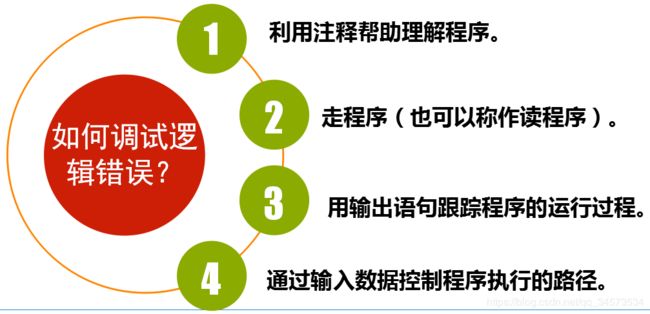
2.调试逻辑错误的方法
1.10 算法分析
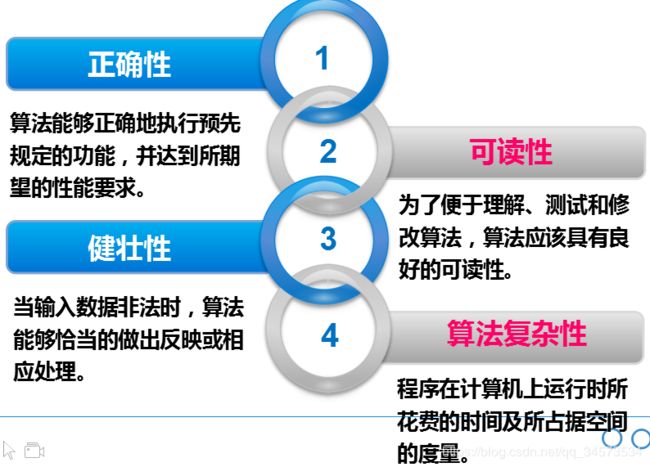
1.算法评价标准
2.算法复杂性
算法复杂性是算法效率的度量,是评价算法优劣的重要依据。一个算法复杂性的高低体现在运行该算法所需要的计算机资源的多少上面,需要的资源越多,算法的复杂性越高;需要的资源越少,算法的复杂性越低。
3.算法复杂性的分类
时间复杂度和空间复杂度。