FPGA数字信号处理(26)加扰器与解扰器设计
加扰与解扰
设计数字通信系统时,必须考虑发送信息的信号特征,这些特征会影响到设计性能。总的来说,发送的信息应注意:(1).避免出现长串的0或1,否则对于从0、1交换点处提取位同步信息的系统,容易错判导致失去同步;(2).避免传输信号具有周期性,否则在多路传输的通信系统中容易造成串扰。
信道编码中的加扰器和解扰器便是完成上述功能,将发送信号处理成没有长传的0或1,并且数字信号最小周期足够长。对信号加扰处理可以使其统计特性接近于高斯白噪声的统计特性,在接收端需要用逆运算解扰恢复出原始发送序列。
加扰器可以采用一个带反馈的移位寄存器生成伪随机序列,对数据进行加扰。需要选择的参数有生成多项式和移位寄存器初始状态(不能是0,否则输入为0时输出恒为0)。如一个加扰器结构如下:
加扰器由移位寄存器和异或门(有些文献中称为模2加法器)组成,选择的生成多项式决定了每级寄存器是否接到异或门中。上图中bk=ak^bk-2^bk-3^bk-4^bk-8,解扰时采用逆运算即可,结构如下所示:

上图中ck=bk^bk-2^bk-3^bk-4^bk-8=ak,恢复出原始数据。
MATLAB设计
使用MATLAB仿真加扰和解扰的过程,代码很简单,如下:
x = randi(2,1,1000)-1; %原始随机序列
%----------------------------------------%
%%% ------------ 加扰器 ------------ %%%
%----------------------------------------%
%scrambler = randi(2,1,8)-1; %加扰器移位寄存器初始状态
scrambler = [0,1,1,0,1,1,1,1];
descrambler = scrambler;
y_scrambler = zeros(1,1000);
for i = 1 : 1000
z(1) = bitxor(scrambler(1),scrambler(5)); %模2加法器(异或)
z(2) = bitxor(z(1),scrambler(6));
z(3) = bitxor(z(2),scrambler(7));
y_scrambler(i) = bitxor(z(3),x(i));
for j = 1 : 7 %移位寄存
scrambler(j) = scrambler(j+1);
end
scrambler(8) = y_scrambler(i);
end
%----------------------------------------%
%%% ------------ 解扰器 ------------ %%%
%----------------------------------------%
y_descrambler = zeros(1,1000);
for i = 1 : 1000
z(1) = bitxor(descrambler(1),descrambler(5)); %模2加法器(异或)
z(2) = bitxor(z(1),descrambler(6));
z(3) = bitxor(z(2),descrambler(7));
y_descrambler(i) = bitxor(z(3),y_scrambler(i));
for j = 1 : 7 %移位寄存
descrambler(j) = descrambler(j+1);
end
descrambler(8) = y_scrambler(i);
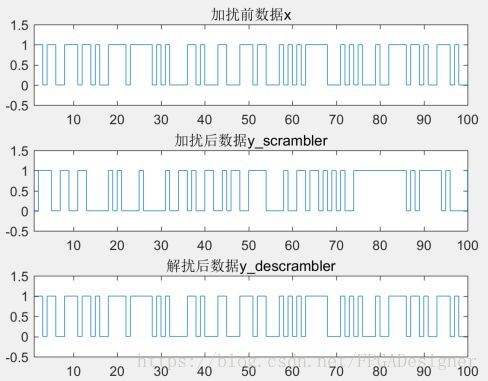
end加扰与解扰结果对比如下(无噪声情况下),可以看到原始数据与解扰后数据完全一致:
为了体现加扰器的功能,将原始序列设置为全1。再次运行结果如下,可以看到加扰器将长传的1转换为了近似随机序列:
FPGA设计
在Vivado中完成算法设计及仿真。该设计很简单,仅仅包含移位寄存器和异或门。异或门在FPGA中会转换为查找表实现,因此整体设计可以在很高的时钟频率下运行。加扰器代码如下:
`timescale 1ns / 1ps
//-------------------------------------------------------------------------
// 加扰器设计,written by刘奇,2018.09.15
//-------------------------------------------------------------------------
module Scrambler
(
input clk,
input rst_n,
input din,
output dout
);
//-------------------------------------------------------------------------
// 移位寄存器部分
//-------------------------------------------------------------------------wire temp;
reg [7:0] scrambler_reg = 8'b11110110; //初始状态
always @ (posedge clk or negedge rst_n)
if (!rst_n) scrambler_reg <= 8'b11110110;
else scrambler_reg <= {temp,scrambler_reg[7:1]};
//-------------------------------------------------------------------------
// 模2加法器设计
//-------------------------------------------------------------------------
assign temp = din ^ scrambler_reg[6] ^ scrambler_reg[5] ^ scrambler_reg[4] ^ scrambler_reg[0];
assign dout = temp;
endmodule解扰器代码如下:
`timescale 1ns / 1ps
//-------------------------------------------------------------------------
// 解扰器设计,written by刘奇,2018.09.15
//-------------------------------------------------------------------------
module Descrambler
(
input clk,
input rst_n,
input din,
input s_tvalid,
output dout
);
//-------------------------------------------------------------------------
// 移位寄存器部分
//-------------------------------------------------------------------------
reg [7:0] descrambler_reg = 8'b11110110; //初始状态
always @ (posedge clk or negedge rst_n)
if (!rst_n) descrambler_reg <= 8'b11110110;
else if (s_tvalid) descrambler_reg <= {din,descrambler_reg[7:1]};
//-------------------------------------------------------------------------
// 模2加法器设计
//-------------------------------------------------------------------------
reg dout_reg;
always @ (posedge clk or negedge rst_n)
if (!rst_n) dout_reg <= 0;
else if (s_tvalid)
dout_reg <= din ^ descrambler_reg[6] ^ descrambler_reg[5] ^ descrambler_reg[4] ^ descrambler_reg[0];
assign dout = dout_reg;
endmodule仿真时将加扰器和解扰器级联在一起,即数据加扰后再进行解扰。原始序列由MATLAB生成并存储在txt文件中,在testbench中读取调用。仿真结果如下图所示,看到原始数据din和解扰输出descrambler_out完全一致,仅有一个时钟周期的延迟:
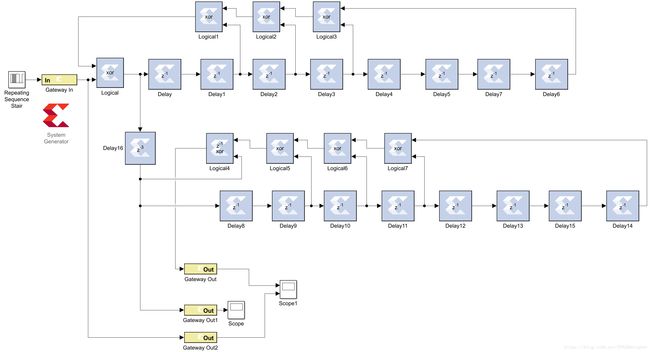
System Generator设计
仿真结果如下图所示,看到原始数据和解扰输出完全一致,只是之间有些延迟: