BPSK系统在瑞利衰落信道下的性能-MATLAB基带仿真

1. 产生一定长度的值为0或1的随机序列$s(t)$。
2. 将$s(t)$映射到BPSK星座图上的星座点。
3. 信号通过衰落信道受到衰落因子$h$的影响，$h$服从瑞利分布。
4. 产生高斯白噪声，将调制后的信号通过AWGN信道，得到输出信号$r(t)$。
5. 利用最小距离判决准则实现检测，统计误比特数。
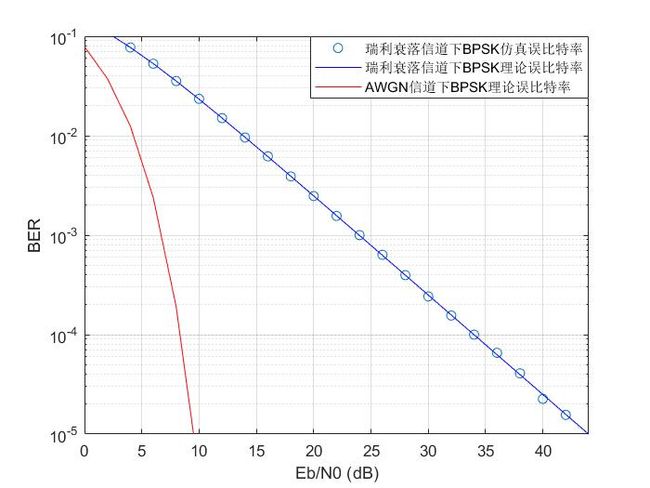
6. 绘制仿真误比特率与理论误比特率曲线，进行对比分析。

瑞利衰落信道
瑞利衰落信道的核心在于乘性衰落因子$h$，用于相干检测的接收信号表示为：

$r(t)=|h|\cdot s(t)+n(t)$

h = (randn(1,L)+1j*randn(1,L))/sqrt(2);	% L为信号长度

其中$\sqrt{2}$为归一化系数，使得$h$方差为1。

这里解释几个问题：

Q：为什么$h$服从瑞利分布？
A：在此篇仿真中，我们认为信道不存在多普勒频移，即FDT=0，同时来波的方向是均匀分布且无穷多的，没有直射分量（若有直射分量，信道衰落系数变为莱斯分布），此时信道衰落系数可等效为瑞利分布。若要考虑多普勒频移的影响，需要建立时间选择性衰落信道，此篇文章方法不适用。

Q：为什么仿真中$h$的方差设置为1？
A：设AWGN信道下BPSK系统平均信噪比为$\frac{E_b}{N_0}$，则瑞利衰落信道下BPSK系统平均信噪比为

${\bar{\gamma }}_b=\frac{E_b}{N_0}E\left(h^2\right)$

为了公平地在一张图中比较BPSK系统在两种信道下的性能差异，要使得仿真中的横坐标，也就是平均信噪比相同，因此设置$h$的方差为1

$D(h^2)=E(h^2)-E^2(h)=E(h^2)-0=E(h^2)$

Q：为什么在仿真中，每一个发送符号都乘了不同的信道衰落系数，信道不是分快衰落和慢衰落吗？
A：实际上，一个相同的$h$持续几个符号，对仿真结果没有影响。我们考察的是统计误码率，只要统计样本足够多，结果是没有变化的。当然在实际问题中，需要考虑信道衰落的平坦与否。

简单评价一下：$h$和$n$对信号的影响有着本质的区别。后者是加性信号，前者是乘性信号，存在对原始信号的放缩作用，因此在利用门限进行判别星座点时，非常容易发生误判。对抗衰落信道的方法有很多，典型的方法有分集等。

BPSK发送端星座图：

相干解调：
最小距离判决准则：

$\hat{s}(t)=\underset{1\le m\le M}{\mathrm{argmin}}\Vert r(t)-s_m(t){\Vert }_2^2$

BPSK在AWGN信道下的理论误比特率：

$P_{b,AWGN}=Q(\sqrt{\frac{2{\mathcal{E}}_b}{N_0}})$

BPSK在瑞利衰落信道下的理论误比特率：

${\bar{\gamma }}_b=\frac{{\mathcal{E}}_b}{N_0}E\left(h^2\right)$ $P_b=\frac{1}{2}(1-\sqrt{\frac{{\bar{\gamma }}_b}{1+{\bar{\gamma }}_b}})$

仿真结果：

MATLAB基带仿真程序：

clc
clear
close all
% Title:BPSK系统在平坦瑞利衰落信道下的性能仿真
% Author：K.X.Song_HIT
% Data: 2019.03.26

L = 5000000;                            % 数据长度
data = round(rand(1,L));                % 原始数据
send = (data - 1/2) * 2;                % BPSK调制
EbN0_dB = 0:2:44;                       % Eb/N0 dB形式
EbN0 = 10.^(EbN0_dB/10);                % Eb/N0
Eb = 1;                                 % 每比特能量
N0 = Eb ./ EbN0;                        % 噪声功率
h = (randn(1,L) + 1j * randn(1,L)) / sqrt(2);       % 衰落因子
error = zeros(1,length(EbN0_dB));                   % 预置错误个数
ber = zeros(1,length(EbN0_dB));                     % 预置仿真误比特率
tber_bpsk = zeros(1,length(EbN0_dB));               % 预置理论误比特率
tber_bpsk_fading = zeros(1,length(EbN0_dB));        % 预置理论误比特率

for q = 1:length(EbN0_dB)
    noise = sqrt(N0(q)/2) * randn(1,L);     % 生成噪声
    receive = abs(h) .* send + noise;       % 接收信号
    detect = zeros(1,L);                % 预置检测信号
    % BPSK解调
    % 注：如果是其他调制方式，下面换成对应的解调方法即可
    for w = 1:L
        if (receive(w) >= 0)
            detect(w) = 1;              % 数轴右侧 ->  1
        else
            detect(w) = -1;             % 数轴左侧 -> -1
        end
        if (detect(w) ~= send(w))
            error(q) = error(q) + 1;    % 错误个数
        end
    end
    ber(q) = error(q) / L;                      % 仿真误比特率
    tber_bpsk(q) = erfc(sqrt(EbN0(q)))/2;       % AWGN信道下BPSK理论误比特率
    tber_bpsk_fading(q) = (1-sqrt(EbN0(q)/(1+EbN0(q))))/2;  % 瑞利衰落信道下BPSK理论误比特率
end
figure
semilogy(EbN0_dB,ber,'o',EbN0_dB,tber_bpsk_fading,'b',EbN0_dB,tber_bpsk,'r');
grid on;
axis([0 44 10^-5 10^-1])
xlabel('Eb/N0 (dB)');
ylabel('BER');
legend('瑞利衰落信道下BPSK仿真误码率','瑞利衰落信道下BPSK理论误码率','AWGN信道下BPSK理论误码率');