关于2019nCoV新冠肺炎的建模（Ⅱ）—基于Logistic模型的疫情预测

引言

模型完成于2月6日，在考虑模型的问题上，笔者主要参考了来自来之csdn的大佬与知网的有关文章，仔细斟酌，确定采用Logistic模型与SEIR带潜伏期传染模型对疫情进行分析与预测。不足之处望读者多加指正。

抓取数据分析

笔者首先对抓取的china_Dailylist中的数据进行简单的分析，提取出表中的data、与每日确诊人数confirm。画出一个简单的趋势图。

#引用约定
import pandas as pd
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']#解决中文乱码问题
from matplotlib import pyplot as plt
import random
import numpy as np
import matplotlib
import collections
from scipy.optimize import curve_fit
import math
#from matplotlib import pyplot as plt
data=pd.read_csv('china_DailyList_2020_02_03.csv')
print(data.head())
x=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]
y=data['confirm']
z=data['heal']
plt.plot(x,y,color='green',marker='o',linestyle='solid',label='疫情确诊人数')
plt.plot(x,z,color='red',marker='o',linestyle='solid',label='治愈人数')
plt.title('疫情趋势图')#加标题
plt.ylabel('患病人数')
plt.xlabel("日期")
plt.show()

这里的x轴日期-笔者是一抓取的数据的开始日期为主，1-25代表的日期的2020-01-23_2020-02-05。

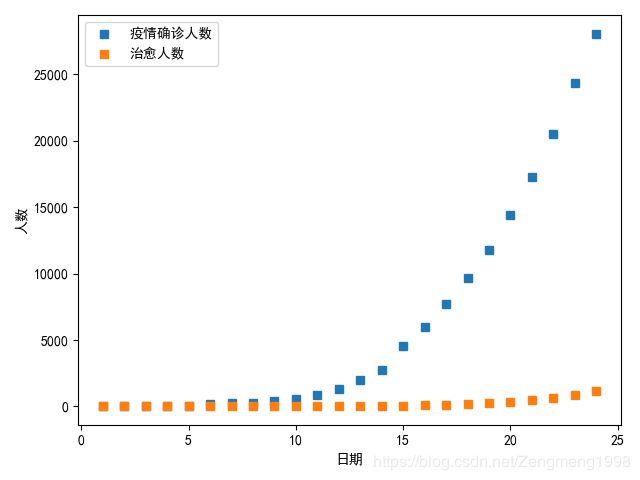
将确诊人数连成一条光滑的曲线可以看见：

plt.plot(x,y,'r',label='疫情确诊人数')
plt.ylabel('人数')
plt.xlabel("日期")
plt.legend(loc=0)
plt.show()

Logistic模型预测

Logistic模型的数学原理笔者在此省略，有兴趣了解可自行百度
简言之就是利用已有的数据，拟合出上述方程，P（t）：人数函数；K：最值；r：增长阻力（如医学隔离导致的疫情增长阻力）。

#logistic模型
# a=0.10
# b=0.60
# eor=100


def logistic_increase_function(t, K, P0, r):
     r=0.29
     t0 = 1
     exp_value = np.exp(r * (t - t0))
     return (K * exp_value * P0) / (K + (exp_value - 1) * P0)
     # 日期与感染人数
t = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]
t = np.array(t)
P = data['confirm']
# 最小二乘拟合
P = np.array(P)
popt, pocv = curve_fit(logistic_increase_function, t, P)
# for i in range(len(P)):
#      print(P[i])
# print(type(P))
# print(type(P))
# print(P)


#所获取的opt皆为拟合系数
print("K:capacity P0:intitial_value r:increase_rate t:time")
print(popt)
#拟合后对未来情况进行预测
P_predict=logistic_increase_function(t,popt[0],popt[1],popt[2])
future=[25,27,29,40,60,71,76,82]
future=np.array(future)
future_predict=logistic_increase_function(future,popt[0],popt[1],popt[2])
#近期情况
tomorrow=[25,26,27,28,29,30,31]
tomorrow=np.array(tomorrow)
tomorrow_predict=logistic_increase_function(tomorrow,popt[0],popt[1],popt[2])
#图像绘制
plot1=plt.plot(t,P,'s',label="疫情确诊感染人数")
plot2=plt.plot(t,P_predict,'r',label='感染人数拟合曲线')
plot3=plt.plot(tomorrow,tomorrow_predict,'s',label='近期感染人数预测')

plt.xlabel('日期')
plt.ylabel('确诊人数')
plt.legend(loc=0)
plt.show()
plot4=plt.plot(future,future_predict,'s',label='未来感染人数预测')
plt.show()
for i in range(25):
     people_sick=int(logistic_increase_function(np.array(i+25),popt[0],popt[1],popt[2]))
     print("2月%d日确诊人数预计:%d人"%(i+6,people_sick))

阻力r的选取

在python中logticis拟合中，不同程度的增长阻力，可以影响曲线拟合好坏与后期结果的选取。r与K的选取在其中都值得考究，出于方便，笔者在此先对r进行讨论
r=0.6时；

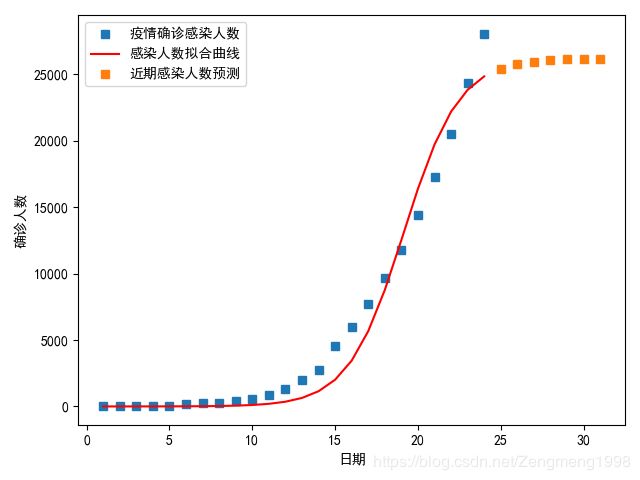
r=0.1时；

拟合结果

笔者认为优化r方法有1.进行网格优化；
2.进行二分优化；（这里笔者取0.29作为优化结果）

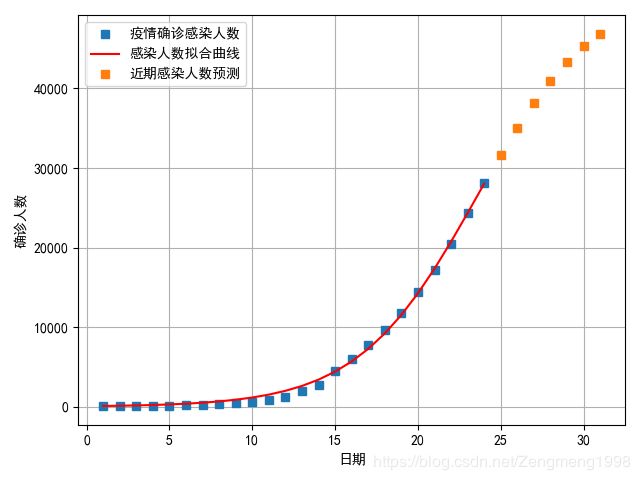
对于未来患者的人数预测，与拐点分析：


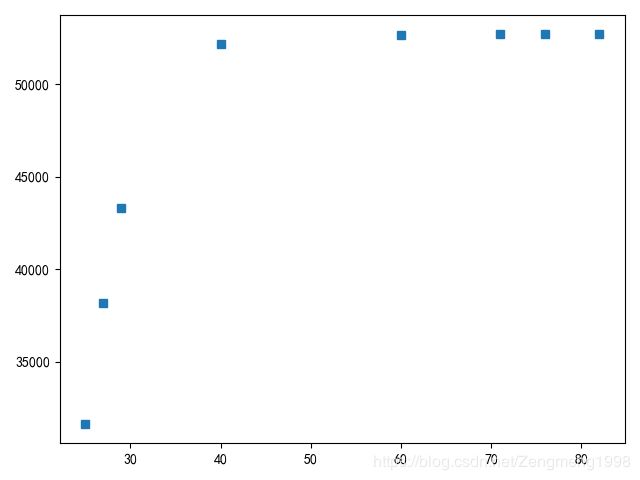
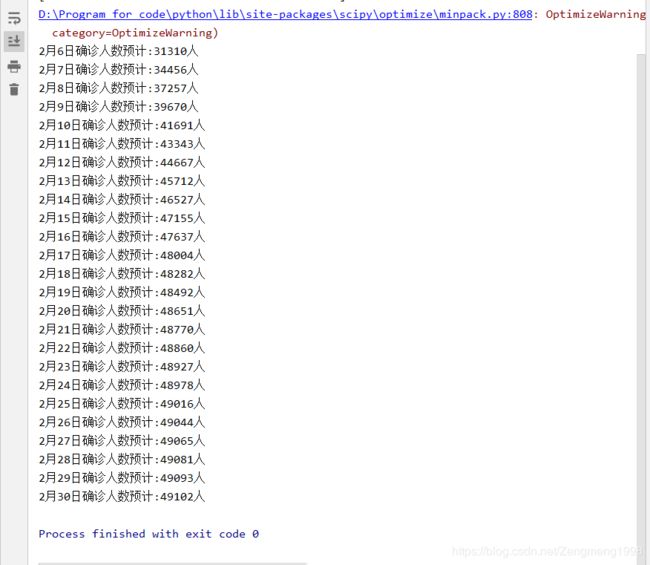
预测拐点的出现日期在2月下旬到3月上旬，患病人数的峰值大约为5万人。

小结

模型选取的方面，Logistic只能大约预计到的拐点的日期与患病人数的峰值，无法预测出疫情的全过程，同时在r与k值得优化问题上仍有待改进。

参考

知网
https://blog.csdn.net/z_ccsdn/article/details/104134358

一段

云栖大会上阿里的一位外国程序员花名小美，讲过这样一段：在中国想结婚得有房子，我准备和东北女朋友结婚，于是去看翡翠城的房子。那个房子是90平的，我的老婆对我说：“这个房子太小啦。”
小美不解，他老婆又说："我不是那个意思啦，我是说，我们以后可能还要添砖加瓦啦？“
小美：“java？什么java？python才是世界上最好的语言啊。”