【找工作学生请进】Dynamic Programming-大厂爱问的动态规划算法面试题视频讲解来啦~
Dynamic Programming
【找工作学生请进】Dynamic Programming-大厂爱问的动态规划算法面试题视频讲解来啦~
DP定义:
动态规划是分治思想的延伸,通俗一点来说就是大事化小,小事化无的艺术。
在将大问题化解为小问题的分治过程中,保存对这些小问题已经处理好的结果,并供后面处理更大规模的问题时直接使用这些结果。
动态规划具备了以下三个特点
- 把原来的问题分解成了几个相似的子问题。
- 所有的子问题都只需要解决一次。
- 储存子问题的解。
动态规划的本质,是对问题状态的定义和状态转移方程的定义(状态以及状态之间的递推关系)
动态规划问题一般从以下四个角度考虑:
- 状态定义
- 状态间的转移方程定义
- 状态的初始化
- 返回结果
状态定义的要求:定义的状态一定要形成递推关系。
一句话概括:三特点四要素两本质
适用场景:最大值/最小值, 可不可行, 是不是,方案个数
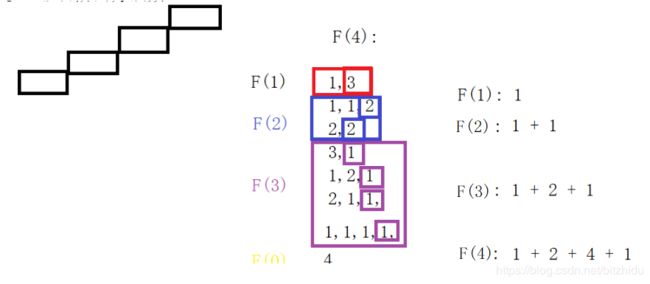
第1题 变态青蛙跳台阶(Climbing Stairs)
- 难度:Easy
- 备注:需要C基础,排列,出自《剑指offer》
- 题目描述
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
int jumpFloorII(int number)
来源:牛客-剑指offer
答案-C/C++
/*
by 周荣
方法一:动态规划
状态:
子状态:跳上1级,2级,3级,...,n级台阶的跳法数
f(n):还剩n个台阶的跳法数
状态递推:
n级台阶,第一步有n种跳法:跳1级、跳2级、到跳n级
跳1级,剩下n-1级,则剩下跳法是f(n-1)
跳2级,剩下n-2级,则剩下跳法是f(n-2)
f(n) = f(n-1)+f(n-2)+...+f(n-n)
f(n) = f(n-1)+f(n-2)+...+f(0)
f(n-1) = f(n-2)+...+f(0)
f(n) = 2*f(n-1)
初始值:
f(1) = 1
f(2) = 2*f(1) = 2
f(3) = 2*f(2) = 4
f(4) = 2*f(3) = 8
所以它是一个等比数列
f(n) = 2^(n-1)
返回结果:f(N)
方法二:排列
每个台阶看成一个位置,除过最后一个位置,其它位置都有两种可能性,
所以总的排列数为2^(n-1)*1 = 2^(n-1)
*/
class Solution {
public:
int jumpFloorII(int number) {
if(number <= 0)
return 0;
int total = 1;
for(int i = 1;i < number;i++)
total *= 2;
return total;
}
};
/*
扩展:降低时间复杂度
上述实现的时间复杂度:O(N)
O(1)的实现:使用移位操作
*/
class Solution {
public:
int jumpFloorII(int number) {
if(number <= 0)
return 0;
return 1<<(number-1);
}
};
/*
总结:
此题看似复杂,通过抽象和归纳,可以找出问题的内在规律
定义问题的状态,以及状态间的递推关系,找到问题的答案
扩展1:
上述问题为变态青蛙跳台阶,太疯狂,这只青蛙像是吃了大力丸
身上充满了无穷的力量。现在让它变成一个正常的青蛙,限制它
一次只能跳1阶或者2阶,现在该如何解答
扩展2:牛客网上另一个题目:矩形覆盖
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。
请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
上述两个题目都可以用斐波那契数列求解。
*/
第2题 最大连续子数组和(Maximum Subarray)
- 难度:Easy
- 备注:出自《剑指offer》
- 题目描述
HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢?例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组,返回它的最大连续子序列的和,你会不会被他忽悠住?(子向量的长度至少是1)
int FindGreatestSumOfSubArray(vector array)
来源:牛客-剑指offer
答案-C/C++
/*
by 周荣
方法:动态规划
状态:
子状态:长度为1,2,3,...,n的子数组和的最大值
F(i):长度为i的子数组和的最大值,这种定义不能形成递推关系,舍弃
F(i):以array[i]为末尾元素的子数组和的最大值
状态递推:
F(i) = max(F(i-1) + array[i],array[i])
F(i) = (F(i-1) > 0)? F(i-1) + array[i] : array[i]
初始值:F(0) = array[0]
返回结果:
maxsum:所有F(i)中的最大值
maxsum = max(maxsum,F(i))
*/
class Solution{
public:
int FindGreatestSumOfSubArray(vector<int> array){
if (array.empty()){
return -1;
}
// F(i)初始化
int sum = array[0];
// maxsum初始化
int maxsum = array[0];
for (int i = 1; i < array.size(); i++){
// F(i) = max(F(i-1) + array[i],array[i])
sum = (sum > 0) ? sum + array[i] : array[i];
// maxsum = max( maxsum,F(i))
maxsum = (sum < maxsum) ? maxsum : sum;
}
return maxsum;
}
};
第3题 三角矩阵(Triangle)
- 难度:Medium
- 备注:出自leetcode
- 题目描述
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
[ [2], [3,4], [6,5,7], [4,1,8,3] ]The minimum path sum from top to bottom is11(i.e., 2 + 3 + 5 + 1 = 11).
int minimumTotal(vector
&triangle) 来源:牛客-leetcode
答案-C/C++
/*
by 周荣
题目描述:
给定一个三角矩阵,找出自顶向下的最短路径和,每一步可以移动到下一行的相邻数字。
比如给定下面一个三角矩阵,自顶向下的最短路径和为11。
方法:动态规划
状态:
子状态:从(0,0)到(1,0),(1,1),(2,0),...(n,n)的最短路径和
F(i,j): 从(0,0)到(i,j)的最短路径和
状态递推:
F(i,j) = min( F(i-1, j-1), F(i-1, j)) + triangle[i][j]
初始值:
F(0,0) = triangle[0][0]
返回结果:
min(F(n-1, i))
*/
class Solution {
public:
int minimumTotal(vector<vector<int>> &triangle) {
if (triangle.empty()){
return 0;
}
// F[i][j], F[0][0]初始化
vector<vector<int>> min_sum(triangle);
int line = triangle.size();
for (int i = 1; i < line; i++){
for (int j = 0; j <= i; j++){
// 处理左边界和右边界
if (j == 0){
min_sum[i][j] = min_sum[i - 1][j];
}
else if (j == i){
min_sum[i][j] = min_sum[i - 1][j - 1];
}
else{
min_sum[i][j] = min(min_sum[i - 1][j], min_sum[i - 1][j - 1]);
}
// F(i,j) = min( F(i-1, j-1), F(i-1, j)) + triangle[i][j]
min_sum[i][j] = min_sum[i][j] + triangle[i][j];
}
}
int result = min_sum[line - 1][0];
// min(F(n-1, i))
for (int i = 1; i < line; i++){
result = min(min_sum[line - 1][i], result);
}
return result;
}
};
/*
方法二:动态规划(反向思维)
状态:
子状态:从(n,n),(n,n-1),...(1,0),(1,1),(0,0)到最后一行的最短路径和
F(i,j): 从(i,j)到最后一行的最短路径和
状态递推:
F(i,j) = min( F(i+1, j), F(i+1, j+1)) + triangle[i][j]
初始值:
F(n-1,0) = triangle[n-1][0], F(n-1,1) = triangle[n-1][1],..., F(n-1,n-1) = triangle[n-1][n-1]
返回结果:
F(0, 0)
这种逆向思维不需要考虑边界,也不需要最后寻找最小值,直接返回F(0,0)即可
*/
class Solution2 {
public:
int minimumTotal(vector<vector<int>> &triangle) {
if (triangle.empty()){
return 0;
}
// F[n-1][n-1],...F[n-1][0]初始化
vector<vector<int>> min_sum(triangle);
int line = triangle.size();
// 从倒数第二行开始
for (int i = line - 2; i >= 0; i--){
for (int j = 0; j <= i; j++){
// F(i,j) = min( F(i+1, j), F(i+1, j+1)) + triangle[i][j]
min_sum[i][j] = min(min_sum[i + 1][j], min_sum[i + 1][j + 1]) + triangle[i][j];
}
}
return min_sum[0][0];
}
};
/*
注:
易错点:只保留每一步的最小值,忽略其他路径,造成最终结果错误
局部最小不等于全局最小
总结:
遇到关于矩阵,网格,字符串间的比较,匹配的问题,
单序列(一维)动规解决不了的情况下,
就需要考虑双序列(二维)动规
*/
讲解视频
下面就是分享的视频咯
点我观看视频讲解哦
本次分享就到这里,如果你从本文收到了启发,可以点赞留言告诉博主
这样我才有动力分享更多的知识咯