最短路径算法--Dijkstra算法，Bellmanford算法，Floyd算法，Johnson算法

最短路径算法

在交通地图上，两地点之间的路径通常标有长度，我们可以用加权有向来描述地图上的交通网。加权有向图中每条路径都有一个路径权值，大小为该路径上所有边的权值之和。本节将重点讨论顶点之间最短路径问题。在实际问题中，路径权值还可以表示其它类型的开销，例如两地之间行程所需要的时间；两任务切换所需代价等。

本节讨论的最短路径具有方向性，问题用图的术语描述为：给定一个起始顶点s和一个结束顶点t，在图中找出从s到t的一条最短路径。称s为路径源点，t为路径汇点。

最短路径问题可以进一步分为单源最短路径和全源最短路径。

l 单源最短路径定义为，给定起始顶点s，找出从s到图中其它各顶点的最短路径。求解单源最短路径的算法主要是Dijkstra算法和Bellman-Ford算法，其中Dijkstra算法主要解决所有边的权为非负的单源最短路径问题，而Bellman-Ford算法可以适用于更一般的问题，图中边的权值可以为负。

l 全源最短路径定义为，找出连接图中各对顶点的最短路径。求解全源最短路径的算法主要有Floyd算法和Johonson算法，其中Floyd算法可以检测图中的负环并可以解决不包括负环的图中的全源最短路径问题；Johonson算法同样也是解决不包含负环的图的全源最短路径问题，但是其算法效率更高。

1 基本原则

最短路径算法具有最短路径的最优子结构性质，也就是两顶点之间的最短路径包括路径上其它顶点的最短路径。具体描述为：对于给定的带权图G=(V, E)，设p=是从v1到vk的最短路径，那么对于任意i和j，1≤i≤j≤k，pij=为p中顶点vi到vj的子路径，那么pij是顶点vi到vj的最短路径。

最短路径算法都使用了松弛(relaxation)技术。开始进行一个最短路径算法时，只知道图中边和权值。随着处理逐渐得到各对顶点的最短路径的信息。算法会逐渐更新这些信息，每步都会检查是否可以找到一条路径比当前给定路径更短。这一过程通常称为“松弛”。

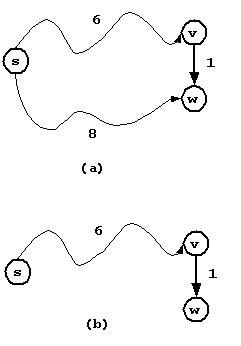
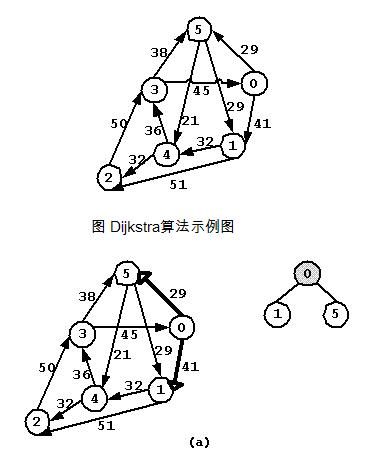
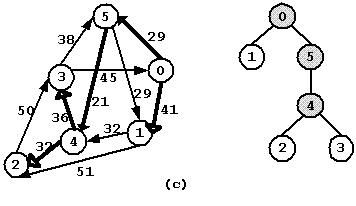
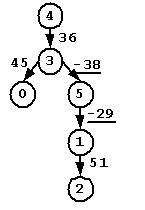
如图为单元最短路径算法的松弛操作。问题为求求解顶点s到图中各顶点之间的最短路径，用d[i]表示顶点s到顶点i的最短路径的长度。对权值为1的边(v, w)进行松弛，若当前到顶点v和w的最短路径的长度分别6和8，如图(a)，则此时d[w]

 

      我们用d[i]数组表示顶点s到顶点i的最短路径的长度，用p[i]表示顶点i在最短路径中的父顶点。可以将边松弛过程用一下代码来描述：

 

Relax(v, w, ω(v, w))
if d[w]>d[v] + ω(v, w)
    {d[w]=d[v] + ω(v, w); p[w] = v;}

 

 2 单源最短路径

单源最短路径定义为，给定起始顶点s，找出从s到图中其它各顶点的最短路径。这里我们将得到的结果称为最短路径树(shortest path tree)，其中树根为起始顶点s。

2.1 Dijkstra算法

在前面章节中讨论最小支撑树时，我们讨论了Prim算法：每次选择一条边添加到最小支撑树MST中，这条边连接当前MST中某个顶点和尚未在MST中的某个顶点，其权值最小。采用类似的方案可以计算最短路径树SPT。开始时将源点添加到SPT中，然后，每次增加一条边来构建SPT，所取的边总是可以给出从源点到尚未在SPT中某个定点的最短路径。这样，顶点按照到源点的距离由小到大逐个添加到SPT中。这种算法称为Dijkstra算法，具体的实现跟Prim类型，分为普通实现和基于最小堆的实现。

首先，我们需要明确Dijkstra算法的适用范围是权值非负的图，即解决带有非负权值的图中的单源最短路径问题。下面对这一属性做简单分析。

给定顶点s，通过Dijkstra算法得到的最短路径树中，从根s到树中各顶点u的树路径对应着图中从顶点s到顶点u的最短路径。归纳证明如下：

假设当前所得到的子树具有这一属性，向当前子树中添加新的顶点u，满足：从顶点s出发，经过当前SPT中的树路径，并最终到达u。可以通过选择，使得所选择的s到u的路径比所有满足条件的路径都更短。所以增加一个新的顶点将增加到达该顶点的一条最短路径。

如果边的权值可以为负数，那么上述证明过程将不成立，上述证明中已经假设了向当前子树中添加新的边时，路径的长度不会递减。然而在具有负权值的边的图中，这个假设不能满足，因为所遇到的任何边都可能指向子树中的某个顶点，而且这条边可能有一个负权值，从而会使得到达该顶点的路径比树路径更短。

以下是Dijkstra算法的实现，Dijkstra算法和基于优先队列的Dijkstra算法都在SingleSourceShortestPaths类中实现，类中包括存放每个顶点到源点的最近距离D数组和存放各个顶点的在SPT中的父节点V数组。

 

 

/*
 * Dijkstra 算法寻找图中单源点最短路径
 * 输入为待寻找的图G以及源点s
 * @param s    起始顶点
  */
public  void Dijkstra( int s){
     if(s < 0)  return;
     int nv = G.get_nv();
     //  初始化
     for( int i = 0; i < nv; i++){
        D[i] = Integer.MAX_VALUE;
        V[i] = -2;
         //  0 没有添加到树中
        G.setMark(i, 0);
    }
    
     //  对起点s，父节点为-1，距离为0
    V[s] = -1;
    D[s] = 0;
    G.setMark(s, 1);
     for(Edge w = G.firstEdge(s); 
            G.isEdge(w); w = G.nextEdge(w)){
        D[G.edge_v2(w)] = G.getEdgeWt(w);
        V[G.edge_v2(w)] = s;
    }

     /* 在其余顶点中找到与当前SPT最近的顶点v，并将
     * 顶点的父节点和顶点v添加到SPT中。其中图的
     * 权值存放在节点v中。
     * 循环迭代，直至所有顶点都遍历一遍. */
     while( true){
         /* 获取与当前树距离最近的边，其终点为最近的顶点
         * 起点为最近顶点的父节点  */
        Edge E = Utilities.minNextEdge(G, V);
         // 如果边为空，函数返回
         if(E ==  null) 
             break;
        System.out.println("ad (" + E.get_v1() + 
                           ", " + E.get_v2() + 
                           "),\t" + G.getEdgeWt(E));

         //  E的终点v被访问过了
         int v = E.get_v2();
        G.setMark(v, 1);
         //  更新与v相连的所有边的距离（松弛过程）
         for(Edge w = G.firstEdge(v); 
                G.isEdge(w); w = G.nextEdge(w)){
             if(D[G.edge_v2(w)] > (D[v] + G.getEdgeWt(w))){
                 //  更新最短距离
                D[G.edge_v2(w)] = D[v] + G.getEdgeWt(w);
                 //  更新父节点
                V[G.edge_v2(w)] = v;
                System.out.println("rx (" + w.get_v1() + 
                           ", " + w.get_v2() + 
                           "),\t" + G.getEdgeWt(w));
            }
        }
    }
    
     //  根据V数组建立最短路径树SPT
    spt.addChild(s, s,  new ElemItem(D[0]));
    spt.setRoot(s);
     int f = -1; 
     //  顶点标记数组，V_idx[i] == 1表示i顶点已经在SPT中，否则不再SPT中
     int[] V_idx =  new  int[V.length];
     //  初始化
     for( int i = 0; i < V_idx.length; i++)V_idx[i] = 0;
     //  起始顶点s已经在SPT中
    V_idx[s] = 1;
     while( true){
        f = -1;
         for( int i = 0; i < V.length; i++){
             //  顶点i不在SPT中，其父顶点V[i]在SPT中，则添加到SPT中
             if(V_idx[i] == 0 && V[i] >= 0 
            && V_idx[V[i]] == 1 && 
            spt.addChild(V[i], i,  new ElemItem(D[i]))){
                V_idx[i] = 1;
                f = 1;
            }
        }
         //  一次都没有添加，结束循环
         if(f == -1)  break;
    }
}

 

算法中每次从SPT之外的顶点中选择一个顶点v，对应边的权值最小；然后对这条边进行松弛操作。算法迭代直至图中所有顶点都在SPT中为止。

以图为例，求解图的最短路径树，起始顶点为顶点0。根据算法实现过程，提取图中最短路径数的过程如图(a-c)。

 

算法初始化阶段每个顶点到起始顶点s的最短路径长度为∞。首先从起始顶点0开始，寻找相邻顶点1和顶点5，并对其进行松弛操作。此时SPT中根节点为0，两个（未确定）子节点为顶点1和顶点5。其中顶点0着色为灰色（赋值1），只有着色为灰色的顶点确定为SPT中顶点。

由于顶点1和顶点5对应的边可能会在以后的操作中进行松弛操作，所以SPT中这两个顶点是未确定的，顶点着色也未改变。

 

    选择与当前SPT中顶点0最近的顶点5，首先将顶点5确定为SPT中顶点0的子节点；然后对其相邻顶点进行松弛操作。相邻顶点为顶点1和顶点4，其中顶点4的最短距离需要更新。

 

选择与当前SPT中顶点0、顶点5最近的顶点4，首先将顶点4确定为SPT中顶点5的子节点；然后对其相邻顶点进行松弛操作。相邻顶点为顶点2和顶点3，这两个顶点都需要更新最短距离。

接下来将先后选择边(5, 1)、(4, 2)和(4, 3)，并进行松弛操作。最终得到的SPT为：

 

将图作为算法代码的测试输入，编写示例程序如下：

 

public  class DijkstraExample {
     public  static  void main(String args[]){
        GraphLnk GL = 
            Utilities.BulidGraphLnkFromFile("Graph\\graph8.txt");
        SingleSourceShortestPaths sp = 
             new SingleSourceShortestPaths(GL);
        sp.Dijkstra(0);
        sp.spt.ford_print_tree();
    }
}

 

算法跟踪顶点选择和边松弛操作的过程， 每个顶点距离起始顶点的最短距离记录在数组D中，顶点的父节点保存在数组V中，最终利用前面章节中讨论的广义树存放SPT。程序运行结果为：

 

● relax (0, 1),    41
● relax (0, 5),    29
○ found (0, 5),    29
● relax (5, 4),    21
○ found (5, 4),    21
● relax (4, 2),    32
● relax (4, 3),    36
○ found (5, 1),    29
○ found (4, 2),    32
○ found (4, 3),    36
6 节点,前序遍历打印：
|—— 0.0(0)
    |—— 41.0(1)
    |—— 29.0(5)
        |—— 50.0(4)
            |—— 82.0(2)
            |—— 86.0(3)

 

结果第一部分为算法将各顶点添加到SPT中以及各条边的松弛操作。第二部分表示算法最终获得的SPT树。读者可以自行对照并理解示例程序的运行结果和上面分析步骤。

在前面章节中，Prim算法可以借助于优先队列（最小堆）来提高效率，这里也可以采用这种策略。具体算法过程其读者自行理解，本书提供该算法的实现，具体参见程序。通过分析可以发现基于最小堆的Dijkstra算法的时间开销与ElgV成正比。

2.2 BellmanFord算法

Bellman-Ford算法诞生于20世纪50年代，对于不包含负环的图，该算法可以简单有效地求解图的单源最短路径问题。算法的基本思路非常简单：以任意顺序考虑图的边，沿着各条边进行松弛操作，重复操作|V|次(|V|表示图中顶点的个数)。

对有向带权图G = (V, E)，从顶点s起始，利用Bellman-Ford算法求解各顶点最短距离，算法描述如下：

for(i = 0; i < |V|; i++)
     for each edge(u, v) ∈  E
        RELAX(u, v)

算法对每条边做松弛操作，并且重复|V|次，所以算法可以在于|V|·|E|成正比的时间内解决单源最短路径问题。算法十分简单，但是在实际中并不被采用，对其做简单的改进就可以得到更高效算法。

我们对算法的正确性做简单分析。设每个顶点距离起始顶点s的最短距离存放在数组D中。

我们首先假设以下命题为真：算法在第i遍处理之后，对于所有顶点u，D[u]不大于s到u且包含i条（或更少）边的最短路径的长度。

根据以上命题，经过|V|-1次迭代后，对所给定的顶点u，D[u]为任何从s到u且包含|V|-1条（或更少）边的最短路径的长度的下界。此时算法可以停止迭代，因为包含|V|条边（或更多）的任何路径将必然有一个环，通过去除这个环将可以找到一条包含|V|-1（或更少）边的路径，该路径长度不大于去环前的路径的长度。所以D[u]同时又是从s到u的最短路径的上界，既然D[u]同时是下界和上界，那么必然是最短路径的长度。

下面我们对上述命题做归纳证明。i为0时，命题自然为成立；假设命题对于i成立，那么对于每个给定的顶点u分两种情况： 

l 在从s到u包含i+1条（或更少）边的路径中，如果其中最短路径长度为i（或更少），那么D[u]不做调整。

l 否则，有一条从s到u且包含i+1条边的路径，其长度比s到u且包含i（或更少）条边的任何路径都短。该路径必然由s先到达某个顶点w的路径再加上边(w, u)所组成。由归纳假设，D[w]是从s到w的最短距离的上边界，而且第i+1遍处理会对各条边进行检查。

所以算法在第i+1遍处理之后，对于所有顶点u，D[u]不大于s到u且包含i条（或更少）边的最短路径的长度

然而算法每遍处理对于各条边都进行检查将是很大的浪费，因为有大量的边并不会导致有效的松弛。事实上，唯一可能导致调整的边仅为某些特定顶点出发的边：这些顶点的值在上一遍处理中发生了变化。

那么可以对算法进行优化，即每遍处理只对特定顶点出发的边做松弛操作。可以将发生变化的顶点的记录下来，在下一遍处理时对一这些顶点为源点的边做松弛操作。我们使用队列结构来存储这些顶点，以下是算法的实现，算法在MinusWeightGraph类中实现，类中包括存放每个顶点到源点的最近距离D数组和存放各个顶点的在SPT中的父节点V数组。

/**
 * Bellman-Ford 算法求解给定图的单源最短路径；
 * 图中边的权值可以是负数。
 *  @param  s    起始顶点
  */
public  void BellmanFord( int s){
     if(s < 0)  return;
     int nv = G.get_nv();
     //  初始化
     for( int i = 0; i < nv; i++){
        D[i] = Double.MAX_VALUE;
        V[i] = -2;
        G.setMark(i, 0);
    }
     //  队列Q
    LinkQueue Q =  new LinkQueue();
     //  起始顶点的距离为0
    D[s] = 0;
     //  将起点s和nv添加到队列中
     int M = Integer.MAX_VALUE;
    Q.enqueue( new ElemItem(s));
    Q.enqueue( new ElemItem(M));
    System.out.print("●");
    Q.printQueue();
     //  迭代过程，直到Q为空
     while(Q.currSize() != 0){
         int f  = -1;
         int v, N = 0;
         while(M == (v = ((Integer)(Q.dequeue().elem)).intValue())){
             if(N++ > nv){ f = 1;  break;}
            Q.enqueue( new ElemItem(M));
        }
        System.out.print("⊙ ");
        Q.printQueue();
         if(f == 1)  break;
         //  对v的所有相连的边e
         for(Edge e = G.firstEdge(v); 
                G.isEdge(e); e = G.nextEdge(e)){
             //  更新e的终点w的距离
             int w = e.get_v2();
             double P = D[v] + G.getEdgeWt(e);
             //  如果w经过v的路径更短，则更新w的距离
             if(P < D[w]){
                D[w] = P;
                 //  将w添加到队列中
                Q.enqueue( new ElemItem(w));
                 //  将w的父节点重置为v
                V[w] = v;
            }
        }
        System.out.print("●");
        Q.printQueue();
    }
    
     //  根据V数组建立最短路径树SPT
    mst.addChild(s, s,  new ElemItem(D[s]));
    mst.setRoot(s);
     int f = -1; 
     //  顶点标记数组，V_idx[i] == 1表示i顶点已经在SPT中，否则不再SPT中
     int[] V_idx =  new  int[V.length];
     //  初始化
     for( int i = 0; i < V_idx.length; i++)V_idx[i] = 0;
     //  起始顶点s已经在SPT中
     V_idx[s] = 1;
     while( true){
        f = -1;
         for( int i = 0; i < V.length; i++){
             //  顶点i不在SPT中，其父顶点V[i]在SPT中，则添加到SPT中
             if(V_idx[i] == 0 && V[i] >= 0 && V_idx[V[i]] == 1 && 
                mst.addChild(V[i], i,  new ElemItem(D[i]))){
                    V_idx[i] = 1;
                    f = 1;
            }
        }
         //  一次都没有添加，结束循环
         if(f == -1)  break;
    }
}

 

算法实现过程中，用无穷大数Integer.MAX_VALUE分离队列中两遍处理的顶点，变量N记录操作了几遍，当N等于顶点个数时算法完成。算法最终广义树形式的SPT。

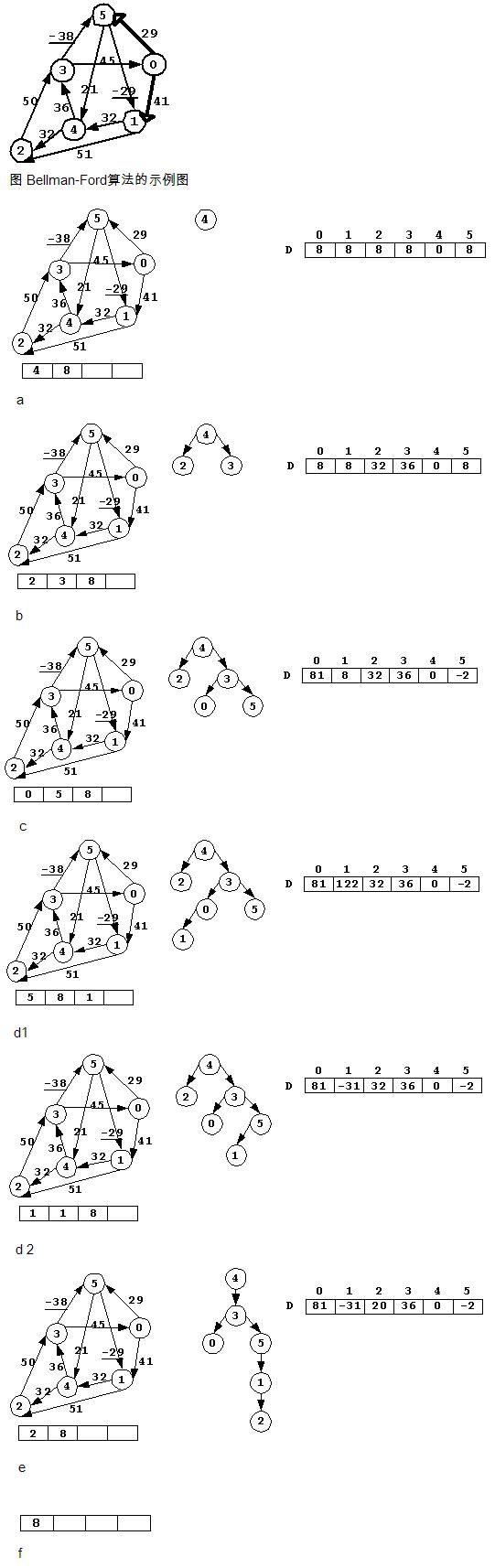
以图为示例，起始顶点为顶点4，根据算法过程，SPT创建过程如图(a~f)，图中记录每遍处理后各顶点的最短距离和队列中的顶点标号。

最终得到的SPT为：

 

 

 

 

图 Bellman-ford算法求解得到的SPT

以图作为示例，编写算法示例程序：

 

 

public  class BellmanFordExample {
     public  static  void main(String args[]){
        GraphLnk GL = 
            Utilities.BulidGraphLnkFromFile("Graph\\graph10.txt");
        MinusWeightGraph MWG =  new MinusWeightGraph(GL);
        MWG.BellmanFord(4);
        System.out.println();
        MWG.mst.ford_print_tree();
    }
}

 

    程序运行结果为：
●队列的元素项从列首到列尾为：
4, 2147483647.
⊙队列的元素项从列首到列尾为：
2147483647.
●队列的元素项从列首到列尾为：
2147483647, 2, 3.
⊙队列的元素项从列首到列尾为：
3, 2147483647.
●队列的元素项从列首到列尾为：
3, 2147483647.
⊙队列的元素项从列首到列尾为：
2147483647.
●队列的元素项从列首到列尾为：
2147483647, 0, 5.
⊙队列的元素项从列首到列尾为：
5, 2147483647.
●队列的元素项从列首到列尾为：
5, 2147483647, 1.
⊙队列的元素项从列首到列尾为：
2147483647, 1.
●队列的元素项从列首到列尾为：
2147483647, 1, 1.
⊙队列的元素项从列首到列尾为：
1, 2147483647.
●队列的元素项从列首到列尾为：
1, 2147483647, 2.
⊙队列的元素项从列首到列尾为：
2147483647, 2.
●队列的元素项从列首到列尾为：
2147483647, 2.
⊙队列的元素项从列首到列尾为：
2147483647.
●队列的元素项从列首到列尾为：
2147483647.
⊙队列为空

6 节点,前序遍历打印：
|—— 0.0(4)
    |—— 36.0(3)
        |—— -2.0(5)
            |—— -31.0(1)
                |—— 20.0(2)
        |—— 81.0(0)

 

 

3 全源最短路径

本节中我们将讨论全源最短路径问题。可以简单地认为全源最短路径问题是单源最短路径问题的推广，即分别以每个顶点作为起始顶点，求其其余顶点到起始顶点的最短距离。例如，在有向非负权值图的中，将每个顶点作为起始顶点，利用Dijkstra算法求解其余顶点到起始顶点的最短距离，算法的时间开销为VElgV。

这里我们将讨论的两种算法针对更为一般的图，图中各条边的权值可以为负数。第一种算法为Floyd算法，针对稠密图，时间开销为V3；第二种算法为Johnson算法，针对稀疏图，该算法结合单源最短路径算法Bellman-Ford算法和Dijkstra算法，算法时间开销为VElogdV。两种算法求解的都是权值可以为负数（不包含负环）的有向带权图。

3.1 Floyd算法

Floyd算法比较简单，通过检查每条边的距离来确定该边是否为一条更短路径的一部分。算法实现如下：

public  class AllPairsShortestPaths {
     //  待处理的图
    GraphLnk G;
     //  V[i][j]表示i在生成树中的父节点
    EdgeElem P[][];
     //  D[i]表示V[i]与i形成的边的权值
     double D[][];
     //  构造函数
     public AllPairsShortestPaths(GraphLnk G){
         this.G = G;
         //  根据G的节点数创建数组
         int V = G.get_nv();
        D =  new  double[V][V];
         //  初始化
         for( int i = 0; i < V; i++)
             for( int j = 0; j < V; j++)
                D[i][j] = Double.MAX_VALUE;
        
        P =  new EdgeElem[V][V];
         for( int i = 0; i < V; i++)
             for( int j = 0; j < V; j++)
                 if(G.isEdge(i, j)){
                     //  将连接边添加到P数组中，更新D数组
                    P[i][j] =  new EdgeElem(
                             new EdgeLnk(i, j,  null), 
                            G.getEdgeWt(i, j));
                    D[i][j] = G.getEdgeWt(i, j);
                }
         //  数组D对角元设为0
         for( int i = 0; i < V; i++) 
            D[i][i] = 0.0;
         //   打印中间结果
         for( int i = 0; i < D.length; i++){
             for( int j = 0; j < D.length; j++){
                 if(D[i][j] != Double.MAX_VALUE)
                    System.out.print(D[i][j] + "\t");
                 else System.out.print("∞\t");
            }
            System.out.println();
        }
        System.out.println("\n------------------------");
    }
    
     /*
     * Floyd 算法，求解全部最短路径算法 O(V^3);
     * 函数没有入参。
      */
     public  void Floyd(){
         int V = G.get_nv();
         for( int i = 0; i < V; i++){
             for( int j = 0; j < V; j++){
                 if(P[j][i] !=  null){
                     for( int t = 0; t < V; t++){
                         //  更新顶点j到顶点t的距离，即D[j][t]
                         if(j != t &&
                          D[j][t] > D[j][i] + D[i][t]){
                            P[j][t] = P[j][i];
                            D[j][t] = D[j][i] + D[i][t];
                            
                             //  打印中间结果
                             for( int i2 = 0; i2 < D.length; i2++){
                                 for( int j2 = 0; j2 < D.length; j2++){
                                     if(D[i2][j2] != Double.MAX_VALUE)
                                        System.out.print(D[i2][j2] + "\t");
                                     else System.out.print("∞\t");
                                }
                                System.out.println();
                            }
                            System.out.println("\n------------------------");
                        }
                    }
                }
            }
        }
    }
}

 

算法通过三重循环实现每对顶点之间的最短路径，如图，对顶点每个i，松弛每条边(j, t)，检查它的距离并确定是否存在更短的路径，并且边(j, i)为该路径中的边。算法实现过程中打印显示i变化过程中每对顶点之间的最短距离。

算法时间开销与V3成正比。算法中用二维数组D存放每对顶点之间的最短距离，例如，D[i][j]表示顶点i到顶点j之间的最短距离；数组P存放顶点顶点的路径，例如，P[i][j]表示顶点i到顶点j之间最短路径中的第一条表，按图索骥可以找到顶点i到j之间最短路径上的每条边。

 

 

 

 

图 Floyd算法三重循环松弛操作

以图（负权图）为示例，编写Floyd算法 测试示例程序：

public  class FloydExample {
     public  static  void main(String args[]){
        GraphLnk GL = 
            Utilities.BulidGraphLnkFromFile("Graph\\graph10.txt");
        AllPairsShortestPaths APSP =  new AllPairsShortestPaths(GL);
        APSP.Floyd();
        
        System.out.println("\n各顶点最短路径：");
         for( int i = 0; i < APSP.D.length; i++){
             for( int j = 0; j < APSP.D.length; j++){
                 if(APSP.P[i][j] !=  null)
                    System.out.print(APSP.P[i][j].get_v1() 
                            + "-->" +APSP.P[i][j].get_v2()
                            + "\t");
                 else
                    System.out.print("-----\t");
            }
            System.out.println();
        }
    }
}
   

 

    程序运行结果如下：
    
    0    41    ∞    ∞    ∞    29    
    ∞    0    51    ∞    32    ∞    
    ∞    ∞    0    50    ∞    ∞    
    45    ∞    ∞    0    ∞    -38    
    ∞    ∞    32    36    0    ∞    
    ∞    -29    ∞    ∞    21    0    
    
    ------------------------
    == 0 ==
    0    41    ∞    ∞    ∞    29    
    ∞    0    51    ∞    32    ∞    
    ∞    ∞    0    50    ∞    ∞    
    45    86    ∞    0    ∞    -38    
    ∞    ∞    32    36    0    ∞    
    ∞    -29    ∞    ∞    21    0    
    
    ------------------------
    == 1 ==
    0    41    92    ∞    73    29    
    ∞    0    51    ∞    32    ∞    
    ∞    ∞    0    50    ∞    ∞    
    45    86    137    0    118    -38    
    ∞    ∞    32    36    0    ∞    
    ∞    -29    22    ∞    3    0    
    
    ------------------------
    == 2 ==
    0    41    92    142    73    29    
    ∞    0    51    101    32    ∞    
    ∞    ∞    0    50    ∞    ∞    
    45    86    137    0    118    -38    
    ∞    ∞    32    36    0    ∞    
    ∞    -29    22    72    3    0    
    
    ------------------------
    == 3 ==
    0    41    92    142    73    29    
    146    0    51    101    32    63    
    95    136    0    50    168    12    
    45    86    137    0    118    -38    
    81    122    32    36    0    -2    
    117    -29    22    72    3    0    
    
    ------------------------
    == 4 ==
    0    41    92    109    73    29    
    113    0    51    68    32    30    
    95    136    0    50    168    12    
    45    86    137    0    118    -38    
    81    122    32    36    0    -2    
    84    -29    22    39    3    0    
    
    ------------------------
    == 5 ==
    0    0    51    68    32    29    
    113    0    51    68    32    30    
    95    -17    0    50    15    12    
    45    -67    -16    0    -35    -38    
    81    -31    20    36    0    -2    
    84    -29    22    39    3    0    
    
    ------------------------
    
    各顶点最短路径
    -----    0-->5    0-->5    0-->5    0-->5    0-->5    
    1-->4    -----    1-->2    1-->4    1-->4    1-->4    
    2-->3    2-->3    -----    2-->3    2-->3    2-->3    
    3-->0    3-->5    3-->5    -----    3-->5    3-->5    
    4-->3    4-->3    4-->3    4-->3    -----    4-->3    
    5-->1    5-->1    5-->1    5-->1    5-->1    -----   

 

结果第一部分为算法过程中记录的每对顶点之间的最短距离，用二维数组的形式返回；第二部分为每对顶点之间最短路径。例如，顶点0到顶点2之间的最短路径，首先取边(0, 5)；然后需要寻找顶点5到顶点2之间最短路径，取边(5, 4)；然后需要寻找顶点4到顶点2之间最短路径，取边(4, 2)，到达顶点2，所以顶点0到顶点2之间的最短路径为，我们可以计算这条路径的长度为ω(0, 5)+ω(5, 4)+ω(4, 2)=29+21+32=82，与距离矩阵D[0][2]相等。

3.2 Johnson算法

Johnson算法可以在O(VElgV)时间内求解每对顶点之间的最短路径。对于稀疏图，该算法在要好于Floyd算法。算法与Floyd算法类似，每对顶点之间的最短距离用二维数组D表示；如果图中存在负环，算法将输出警告信息。Johnson算法把Bellman-Ford算法和Dijkstra算法作为其子函数。

在本节一开始我们提到，如果以每个顶点作为起始顶点，用Dijkstra算法求解单源最短路径，则可以求解全源最短路径，算法复杂度为VElgV。但是对含有负权值的图，Dijkstra算法将失效。Johnson算法运用了“重赋权”技术，即将原图中每条边的权值ω重新赋值为ω’，并且具有以下两个性质：

l 对所有顶点对u,v，路径p是以权值为ω的原图的最短路径，当且仅当路径p也是以权值为ω’的图的最短路径；

l 对于所有的边(u, v)，ω’(u, v)是非负数。

重赋权后的图可以利用Dijkstra算法求解任意两个顶点之间的最短路径。稍后我们将会看到，重赋值不会改变最短路径，其处理复杂度为O(VE)。

下面我们将构造运算使得重赋权操作后得到的新的权值ω’满足上面提及的两个性质。

对带权有向图G=(V, E)，边(u, v)的权值ω(u, v)，设h为顶点映射到实数域的映射函数。对图中每条边(u, v)，定义：

ω'(u, v) = ω(u, v) + h(u) – h(v)

在这样的构造运算可以满足第一条性质，即如果路径p=是权值ω条件下顶点v0到vk的最短路径，那么p也是新权值ω’条件下的最短路径。用lenω(p)表示路径p在原图中的长度，lenω’(p)表示路径p在重赋权后的图中的长度，则

lenω’(p) = ω'(v0, v1) +ω'(v1, v2) + … + ω'(vk-1, vk)

  = [ω(v0, v1) + h(v0) - h(v1)] + [ω(v1, v2) + h(v1) – h(v2)]

+ … + [ω(vk-1, vk) + h(vk-1) – h(vk)]

  = ω(v0, v1) + ω(v1, v2) + … + ω(vk-1, vk) + h(v0) – h(vk)

  = lenω(p) + h(v0) – h(vk)

所以，如果权值为ω条件下顶点v0到vk存在一条更短的路径p*，那么对应地，在以权值为ω’的条件下，路径p*也比路径p更短。

再考虑第二条性质，即保证重赋权后权值非负。我们做如下的构造运算：

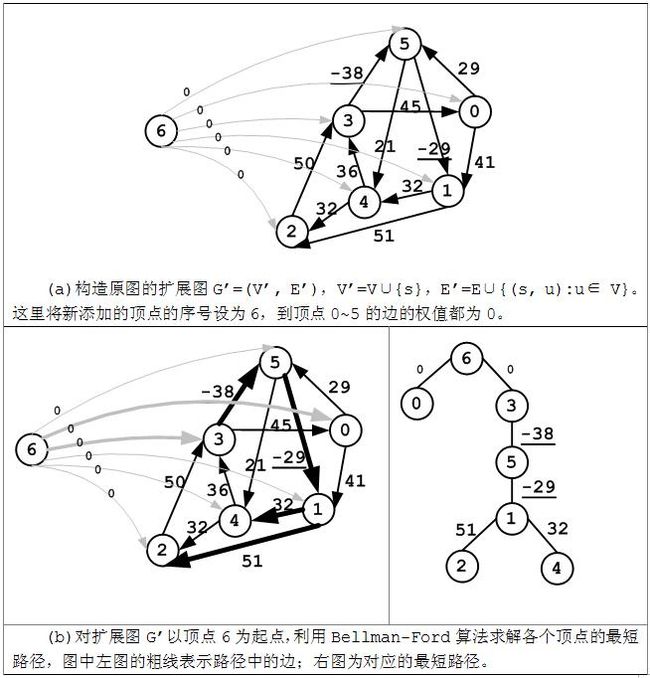
对给定的图G=(V, E)，，边(u, v)的权值ω(u, v)，构造一个新的图G’=(V’, E’)，其中一个新的顶点s∉V，V’=V∪{s}，E’=E∪{(s, u):u∈ V}，对所有的u∈V，ω(s, u)=0。G’中没有以顶点s为终点的边，所以，如果G中不存在负环，那么G’中也不会存在负环。

在不存在负环的前提下，定义h(u)=lenmin(s, u)，即顶点s到顶点u的最短路径，那么对所有的边(v, u)∈V’，h(u)≦ h(v) + ω(v, u)。那么在h(u)=lenmin(s, u)的条件下，便可满足ω'(u, v) = ω(u, v) + h(u) – h(v) ≧ 0，这样第二条性质便可满足。在上一节中我们讨论的Bellman-Ford算法能求解无负环的单元最短路径问题，可以用于求解h函数，其算法复杂度为O(VE)。

根据上面的讨论，Johnson算法结合Bellman-Ford算法和Dijkstra算法，包括以下几个步骤：

l 构造原图的扩展图G’=(V’, E’)，V’=V∪{s}，E’=E∪{(s, u):u∈ V}；

l 在G’中以s为起始顶点应用Bellman-Ford算法，求解各顶点到顶点s的最短路径；

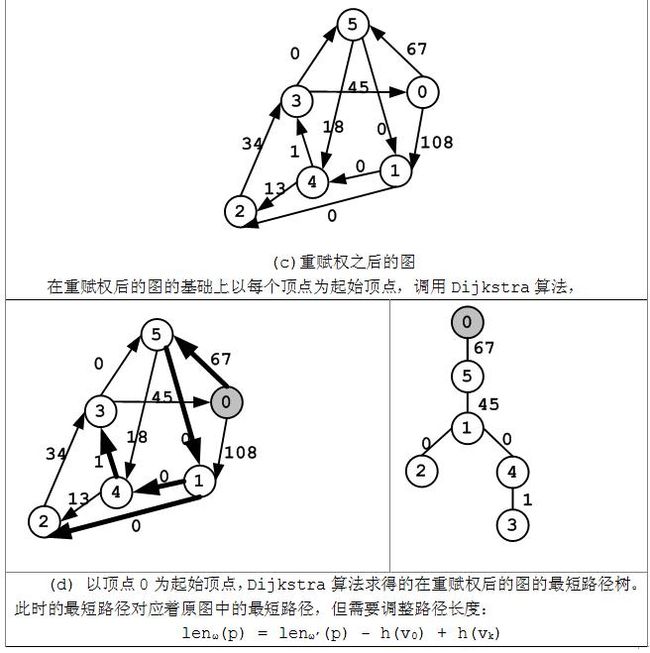
l 对原图重赋权；

l 重赋权后以图中每个顶点为起始顶点，应用Dijkstra算法求解每对顶点之间的最短路径；

l 由于重赋权改变了图中路径的长度，最后需要还原上一步骤中求得最短路径的长度；

根据以上步骤，算法的实现如下：

 

 

public  class JohnsonAlgo {
     double D[][];
     int P[][];
    GraphLnk G;
    
     /**
     * 构造函数
      */
     public JohnsonAlgo(GraphLnk G) {
         this.G = G;
        D =  new  double[G.get_nv()][G.get_nv()];
        P =  new  int[G.get_nv()][G.get_nv()];
    }
    
     public  boolean Johnson(){
         //  创建一个图_G
        GraphLnk _G =  new GraphLnk(G.get_nv() + 1);
         for( int i = 0; i < G.get_nv(); i++){
             for(Edge e = G.firstEdge(i); 
                G.isEdge(e); e = G.nextEdge(e))
                _G.setEdgeWt(e.get_v1(), e.get_v2(), G.getEdgeWt(e));
        }
        
         //  在原图的基础上添加一个顶点ad
         int ad = _G.get_nv() - 1;
         for( int i = 0; i < G.get_nv(); i++){
            _G.setEdgeWt(ad, i, 0);
        }
        
          //  首先调用Bellman-Ford算法，以ad为起始点
        MinusWeightGraph swg =  new MinusWeightGraph(_G);
        swg.BellmanFord(ad);
        
         //  h函数
         int h[] =  new  int[G.get_nv() + 1];
        System.out.println("Bellman-Ford算法结果：");
         for( int i = 0; i < _G.get_nv(); i++)
            System.out.print((h[i] = ( int)swg.D[i]) + "\t");
        System.out.println();
        
         for( int i = 0; i < _G.get_nv() - 1; i++)
             for(Edge e = G.firstEdge(i); 
                G.isEdge(e); e = G.nextEdge(e))
                 //  检测有没有负环
                 if(h[e.get_v2()] > h[e.get_v1()] + _G.getEdgeWt(e))
                {
                    System.out.println("图中有负环。");
                     return  false;
                }
                 //  如果没有则重赋权
                 else{
                     int u = G.edge_v1(e), v = G.edge_v2(e);
                     int wt = ( int) (G.getEdgeWt(e) + 
                            h[G.edge_v1(e)] - h[G.edge_v2(e)]);
                    G.setEdgeWt(u, v, wt);
                }
        System.out.println("重赋权后的各条边的权值：");
         for( int u = 0; u < G.get_nv(); u++){
             for(Edge e = G.firstEdge(u); 
                G.isEdge(e);
                e = G.nextEdge(e)){
                System.out.print(u + "-" + e.get_v2() + 
                        " " + G.getEdgeWt(e) + "\t");
            }
            System.out.println();
        }
        
         //  Dijkstra 算法求解每一个顶点的最短路径树
        SingleSourceShortestPaths sssp = 
                         new SingleSourceShortestPaths(G);
         for( int i = 0; i < G.get_nv(); i++){
            sssp.Dijkstra(i);
            System.out.println("\n第" + i + "顶点Dijkstra结果：");
             for( int j = 0; j < G.get_nv(); j++){
                System.out.print(sssp.D[j] + "\t");
                D[i][j] = sssp.D[j] + h[j] - h[i];
                P[i][j] = sssp.V[j];
            }
            System.out.println();
        }
         return  true;
    }
}

 

根据算法描述步骤和实现代码，以图为例，算法的具体过程如图(a~i)：

 

 

Bellman-Ford算法求解得到各个顶点的最短路径的长度对应这顶点的h函数的映射值，分别为：h(0)=0, h(1)=-67, h(2)=-16, h(3)=0, h(4)=-35, h(5)=-38, h(6)=0.

接下来根据各顶点的h函数值对原图G进行重赋权操作:

ω'(u, v) = ω(u, v) + h(u) – h(v)

过程为：

ω'(0, 1) = (41) + (0) - (-67) = 108

ω'(0, 5) = (29) + (0) - (-38) = 67

ω'(1, 2) = (51) + (-67) - (-16) = 0

ω'(1, 4) = (32) + (-67) - (-35) = 0

ω'(2, 3) = (50) + (-16) - (0) = 34

ω'(3, 0) = (45) + (0) - (0) = 45

ω'(3, 5) = (-38) + (0) - (-38) = 0

ω'(4, 2) = (32) + (-35) - (-16) = 13

ω'(4, 3) = (36) + (-35) - (0) = 1

ω'(5, 1) = (-29) + (-38) - (-67) = 0

ω'(5, 4) = (21) + (-38) - (-35) = 18

得到的图为：

 

 

 各个顶点调整：

D[0][0] = (0) - (0) + (0) = 0

D[0][1] = (67) - (0) + (-67) = 0

D[0][2] = (67) - (0) + (-16) = 51

D[0][3] = (68) - (0) + (0) = 68

D[0][4] = (67) - (0) + (-35) = 32

   D[0][5] = (67) - (0) + (-38) = 29

 

 

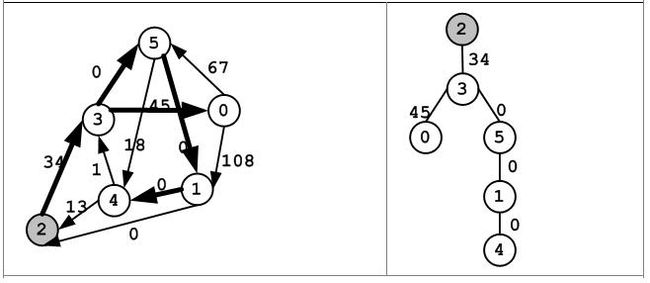
(e) 以顶点1为起始顶点，Dijkstra算法求得的在重赋权后的图的最短路径树。此时的最短路径对应着原图中的最短路径，但需要调整路径长度，各个顶点调整：

D[1][0] = (46) - (-67) + (0) = 113

D[1][1] = (0) - (-67) + (-67) = 0

D[1][2] = (0) - (-67) + (-16) = 51

D[1][3] = (1) - (-67) + (0) = 68

D[1][4] = (0) - (-67) + (-35) = 32

   D[1][5] = (1) - (-67) + (-38) = 30

 

 

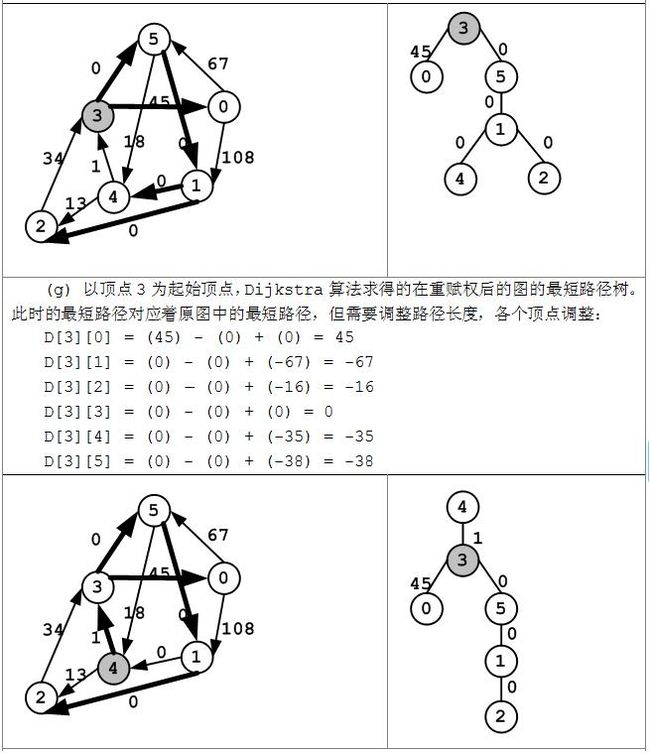
(f) 以顶点2为起始顶点，Dijkstra算法求得的在重赋权后的图的最短路径树。此时的最短路径对应着原图中的最短路径，但需要调整路径长度，各个顶点调整：

D[2][0] = (79) - (-16) + (0) = 95

D[2][1] = (34) - (-16) + (-67) = -17

D[2][2] = (0) - (-16) + (-16) = 0

D[2][3] = (34) - (-16) + (0) = 50

D[2][4] = (34) - (-16) + (-35) = 15

 

 

   D[2][5] = (34) - (-16) + (-38) = 12

 

 

 

 

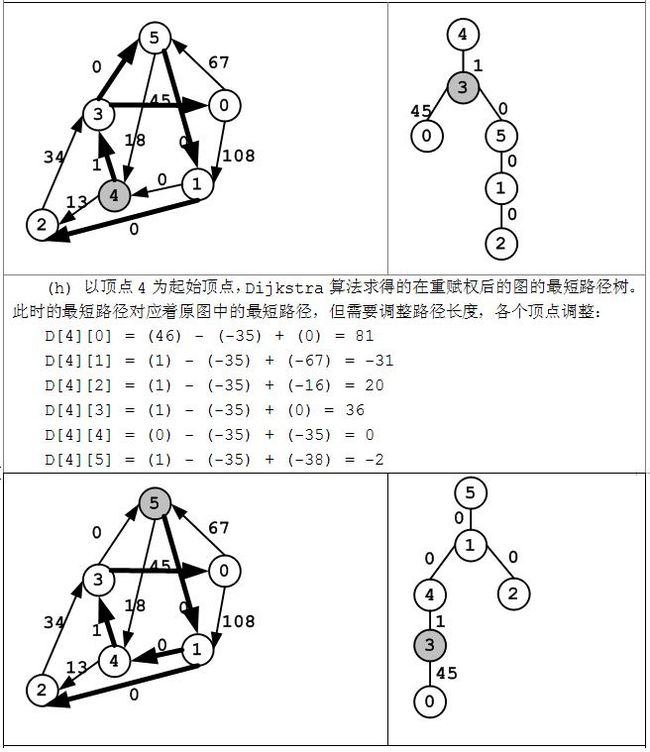
(i) 以顶点5为起始顶点，Dijkstra算法求得的在重赋权后的图的最短路径树。此时的最短路径对应着原图中的最短路径，但需要调整路径长度，各个顶点调整：

D[5][0] = (46) - (-38) + (0) = 84

D[5][1] = (0) - (-38) + (-67) = -29

D[5][2] = (0) - (-38) + (-16) = 22

D[5][3] = (1) - (-38) + (0) = 39

D[5][4] = (0) - (-38) + (-35) = 3

   D[5][5] = (0) - (-38) + (-38) = 0

 

算法最终得到各顶点之间的最短路径及路径长度为：

每对顶点之间的最短路径长度：

	0	1	2	3	4	5
0	0	0	51	68	32	29
1	113	0	51	68	32	30
2	95	-17	0	50	15	12
3	45	-67	-16	0	-35	-38
4	81	-31	20	36	0	-2
5	84	-29	22	39	3	0

每对顶点之间的最短路径:

	0	1	2	3	4	5
0	-1	5	1	4	1	0
1	3	-1	1	4	1	3
2	3	5	-1	2	1	3
3	3	5	1	-1	1	3
4	3	5	1	4	-1	3
5	3	5	1	4	1	-1

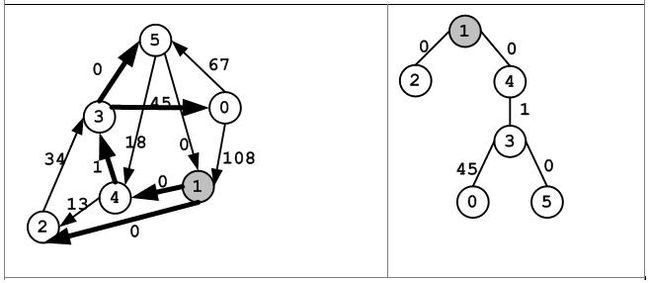
一对顶点之间的最短路径的表中第i行第j列的表项，表示顶点i到顶点j的最短路径中顶点j的父节点。例如，找顶点5到顶点0之间的最短路径时，首先找到顶点3；再找顶点5到顶点3的最短路径，找到顶点4；再找顶点5到顶点4的最短路径，找到顶点1；再找顶点5到顶点1的最短路径，找到顶点5，所以顶点5到顶点0的最短路径为。

以图为例，编写算法程序的示例：

 

public  class JohnsonExample {
     public  static  void main(String args[]){
        GraphLnk g_minus = 
            Utilities.BulidGraphLnkFromFile("Graph\\graph10.txt");

        JohnsonAlgo ja =  new JohnsonAlgo(g_minus);
        ja.Johnson();
        System.out.println("每对顶点之间的最短路径长度：");
         for( int i = 0; i < g_minus.get_nv(); i++){
             for( int j = 0; j < g_minus.get_nv(); j++){
                System.out.print(( int)ja.D[i][j] + "\t");
            }
            System.out.println();
        }
        System.out.println("每对顶点之间的最短路径:");
         for( int i = 0; i < g_minus.get_nv(); i++){
             for( int j = 0; j < g_minus.get_nv(); j++){
                System.out.print(ja.P[i][j] + "\t");
            }
            System.out.println();
        }
    }
}

 

    程序运行部分结果如下：
    
    Bellman-Ford算法结果：
    0    -67    -16    0    -35    -38    0
    7 节点,前序遍历打印：
    |—— 0.0(6)
        |—— 0.0(0)
        |—— 0.0(3)
            |—— -38.0(5)
                |—— -67.0(1)
                    |—— -16.0(2)
                    |—— -35.0(4)
    重赋权后的各条边的权值：
    0-1 108    0-5 67    
    1-2 0    1-4 0    
    2-3 34    
    3-0 45    3-5 0    
    4-2 13    4-3 1    
    5-1 0    5-4 18    
    第0顶点Dijkstra结果：
    0.0    67.0    67.0    68.0    67.0    67.0    
    6 节点,前序遍历打印：
    |—— 0.0(0)
        |—— 67.0(5)
            |—— 67.0(1)
                |—— 67.0(2)
                |—— 67.0(4)
                    |—— 68.0(3)
    第1顶点Dijkstra结果：
    46.0    0.0    0.0    1.0    0.0    1.0    
    6 节点,前序遍历打印：
    |—— 0.0(1)
        |—— 0.0(2)
        |—— 0.0(4)
            |—— 1.0(3)
                |—— 1.0(5)
                |—— 46.0(0)
    第2顶点Dijkstra结果：
    79.0    34.0    0.0    34.0    34.0    34.0    
    6 节点,前序遍历打印：
    |—— 0.0(2)
        |—— 34.0(3)
            |—— 34.0(5)
                |—— 34.0(1)
                    |—— 34.0(4)
            |—— 79.0(0)
    第3顶点Dijkstra结果：
    45.0    0.0    0.0    0.0    0.0    0.0    
    6 节点,前序遍历打印：
    |—— 0.0(3)
        |—— 45.0(0)
        |—— 0.0(5)
            |—— 0.0(1)
                |—— 0.0(2)
                |—— 0.0(4)
    第4顶点Dijkstra结果：
    46.0    1.0    1.0    1.0    0.0    1.0    
    6 节点,前序遍历打印：
    |—— 0.0(4)
        |—— 1.0(3)
            |—— 1.0(5)
                |—— 1.0(1)
                    |—— 1.0(2)
            |—— 46.0(0)
    第5顶点Dijkstra结果：
    46.0    0.0    0.0    1.0    0.0    0.0    
    6 节点,前序遍历打印：
    |—— 0.0(5)
        |—— 0.0(1)
            |—— 0.0(2)
            |—— 0.0(4)
                |—— 1.0(3)
                    |—— 46.0(0)
    每对顶点之间的最短路径长度：
    0    0    51    68    32    29    
    113    0    51    68    32    30    
    95    -17    0    50    15    12    
    45    -67    -16    0    -35    -38    
    81    -31    20    36    0    -2    
    84    -29    22    39    3    0    
    每对顶点之间的最短路径:
    -1    5    1    4    1    0    
    3    -1    1    4    1    3    
    3    5    -1    2    1    3    
    3    5    1    -1    1    3    
    3    5    1    4    -1    3    
    3    5    1    4    1    -1   

 

 

结果每个部分分别对应着算法中的各个步骤，读者可以结合算法步骤以及上面分析的算法过程对结果做进一步理解。