运筹优化学习06:拉格朗日松弛算法(一)
Guignard M. Lagrangean relaxation[J]. TOP, 2003, 11(2):151-200.
摘要
This paper reviews some of the most intriguing results and questions related to Lagrangean relaxation. It recalls essential properties of the Lagrangean relaxation and of the Lagrangean function, describes several algorithms to solve the Lagrangean dual problem, and considers Lagrangean heuristics, ad-hoc or generic, because these are an integral part of any Lagrangean approximation scheme. It discusses schemes that can potentially improve the Lagrangean relaxation bound, and describes several applications of Lagrangean relaxation, which demonstrate the flexibility of the approach, and permit either the computation of strong bounds on the optimal value of the MIP problem, or the use of a Lagrangean heuristic, possibly followed by an iterative improvement heuristic. The paper also analyzes several interesting questions, such as why it is sometimes possible to get a strong bound by solving simple problems, and why an a-priori weaker relaxation can sometimes be “just as good” as an a-priori stronger one.
本论文回顾了一些与拉格朗日松弛相关十分有趣的结论和问题。它回顾了朗格朗日函数和拉格朗日松弛的最本质的特征,描述了拉格朗日对偶问题,并考虑了拉格朗日启发式,不失特殊性和一般性,因为他们是任何拉格朗日近似方案的组成部分。讨论了方案对拉格朗日松弛边界的潜在改善能力,描述了朗格朗日松弛的一些应用来说明这一算法的灵活性,允许计算一些混合整数规划问题的强边界,或者使用拉格朗日启发式算法进行迭代改进。论文也讨论了许多有趣的问题,诸如为什么可以通过求解一个简单的问题得到一个强边界,为什么一个先验的弱约束有时与先验强约束的效果差不多。
引言
Why use Lagrangean relaxation for integer programming problems? How does one construct a Lagrangean relaxation? What tools are there to analyze the strength of a Lagrangean relaxation? Are there more powerful extensions than standard Lagrangean relaxation, and when should they be used? Why is it that one can sometimes solve a strong Lagrangean relaxation by solving trivial subproblems? How does one compute the Lagrangean relaxation bound? Can one take advantage of Lagrangean problem decomposition? Does the “strength” of the model used make a difference in terms of bounds? Can one strengthen Lagrangean relaxation bounds by cuts, either kept or dualized? How can one design a Lagrangean heuristic? Can one achieve better results by remodeling the problem prior to doing Lagrangean relaxation? These are some of the questions that this paper attempts to answer.
本文将回答以下问题:
- 在整数规划问题中为什么要使用拉格朗日松弛呢?
- 如何构建一个拉格朗日松弛?
- 有什么工具可以分析拉格朗日松弛的强度?
- 标准拉格朗日松弛算法有哪些比较有效的拓展,什么时候应用他们呢?
- 为什么有时可用通过求解一个不起眼的子问题就可以解决一个强拉格朗日松弛问题?
- 如何计算拉格朗日松弛边界?
- 拉格朗日分解有哪些优势呢?
- 一个强拉格朗日松弛能够以保持或对偶的方式被切割?
- 如何设计一个拉格朗日启发式算法?
- 在做拉格朗日松弛之前重构问题模型可以得到一个好的结果吗?
The papers starts with a description of relaxations, in particular Lagrangean relaxation (LR for short). It continues with the geometric interpretation of LR, and shows how this geometric interpretation is the best tool for analyzing the effectiveness of a particular LR scheme. Extensions of LR are also reviewed: Lagrangean decomposition and more generally substitution. The Integer Linearization Property is described in detail, as its detection may considerably reduce the computational burden.
文章从松弛的描述,特别是拉格朗日松弛(LR)开始,给出了拉格朗日松弛的几何解释,并认为这种几何解释是分析特定拉格朗日松弛方案有效性的最好工具。也回顾了拉格朗日松弛的拓展问题:拉格朗日分解和更通用的子课题。详细描述了可以大大降低计算成本的整数线性属性(Interger Linearization Property)。
The next section concentrates on solution methods for the dual problem, starting with subgradient optimization, and following with methods based on Lagrangean properties: cutting planes (or constraint generation), Dantzig-and-Wolfe (or column generation), the volume algorithm, bundle and augmented Lagrangean methods, as well as some hybrid approaches.
接着,聚焦对偶问题的解决方法,从次梯度优化到具有拉格朗日特性的割平面法(或约束生成)、Dantzig-and-Wolfe算法(列生成方法)、 the volume algorithm(体算法)、 bundle and augmented Lagrangean methods(束与增广拉格朗日方法)、以及一些混合方法。也回顾了对设计高效优化方法至关重要的拉格朗日函数的一些特征。
This follows the review of some characteristics of the Lagrangean function,important for the design of efficient optimization methods. Cuts that are violated by Lagrangean solutions appear to contain additional information, not captured by the Lagrangean model, and imbedding them in the Lagrangean process may a priori appear to be a good idea. They can either be dualized in Relax-and-Cut schemes, preserving the structure of the Lagrangean subproblems, or appended to the other kept constraints, but at the cost of possibly making the Lagrangean subproblems harder to solve. The next section reviews the conditions for bound improvement under both circumstances.
违背拉格朗日解决方案的切割包含着一些不为拉格朗日模型所囊括的额外信息,将其嵌入到拉格朗日过程中也许可以提前得到一些好点子。如保留朗格朗日子问题结构的对偶松弛和切割方案,或者是增加其他的约束;但潜在的成本是朗格朗日子问题的求解变的更难。接着又综述两种方式对边界的改善情况。
The following section is devoted to Lagrangean heuristics, which complement Lagrangean bounding by making an attempt at transforming infeasible Lagrangean solutions into good feasible solutions.
后续的章节分析了朗格朗日启发,通过尝试变换不可行的朗格朗日子方案为可行的解决方案,以获取朗格朗日边界。
Several applications are reviewed throughout the paper, with emphasis on the steps followed either to re-model the problem or to relax it in an efficient manner.
一些应用也贯穿论文的始终,要么是强调问题模型的重构、要么是以有效的方式放松约束。
The literature on Lagrangean relaxation, its extensions and applications is enormous. As a consequence no attempt has been made here to quote every possible paper dealing with Lagrangean relaxation. Instead, we only list papers that we mention in the text because they directly relate to the material covered here, as they introduced novel ideas or presented new results, new modeling and decomposition approaches, or new algorithms. Finally, we refer the reader to a few pioneer and/or survey papers on Lagrangean relaxation, as they may help get a clearer picture of the whole field.
朗格朗日松弛、拓展问题及其应用的文献不胜枚举,我们从不尝试引证每一篇相关的文献成果。反之,我只列举与材料覆盖直接相关论文,因为它们提出了新的理念或展示了新的成果、模型和分解方法或算法。最后,我们引用了一些拉格朗日松弛的综述论文,帮助你清晰的一览拉格朗日松弛的全貌。主要文献如下:
- Everett (1963),
- Held and Karp (1970),
- Held and Karp (1971),
- Geoffrion (1974),
- Shapiro (1974),
- Shapiro (1979),
- Fisher (1981),
- Fisher (1985),
- Beasley (1993), and Lemar´ echal (2001)
符号及描述
如果P是一个优化问题,则可定义如下记号:
| FS(P) | 问题P的可行解集 |
| OS(P) | 问题P的优化界集 |
| v(P) | 问题P的最优解 |
| x的转置 | |
| 某个多面体的第k个极点 | |
| 第k次迭代得到的解决方案 | |
| co(X) | 集合X的凸包 |
| 第k次迭代的 |
松弛优化问题
Geoffrion(1974)正式定义了一个最小化问题的松弛问题。
定义:若问题![]() 是与问题
是与问题![]() 具有相同决策变量的一个松弛问题,当且仅当:
具有相同决策变量的一个松弛问题,当且仅当:
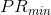 的可行解集包含
的可行解集包含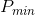 的可行解集,即
的可行解集,即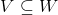
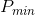 的可行解中,
的可行解中,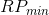 的目标函数要优于
的目标函数要优于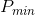 ,即
,即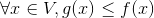
显然,![]() ,换言之,
,换言之,![]() 是问题
是问题![]() 的优化版本,可以提供问题
的优化版本,可以提供问题![]() 的下界,具有更小的最小值。
的下界,具有更小的最小值。
当然,如果原始问题是一个求最大值的问题,则定义可变换为:
若问题![]() 是与问题
是与问题![]() 具有相同决策变量的一个松弛问题,当且仅当:
具有相同决策变量的一个松弛问题,当且仅当:
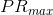 的可行解集包含
的可行解集包含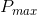 的可行解集,即
的可行解集,即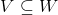
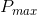 的可行解中,
的可行解中,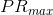 的目标函数要优于
的目标函数要优于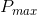 ,即
,即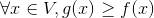
显然,![]() ,换言之,
,换言之,![]() 是问题
是问题![]() 的优化版本,可以提供问题
的优化版本,可以提供问题![]() 的上界,具有更大的最大值
的上界,具有更大的最大值
接下来的讲述,我们不区分最大值和最小值问题,两个问题可以根据如下形式进行转换:
![]()
对问题进行松弛具有两个好处:第一,它提供了困难优化问题的边界;第二,对于解决方案而言,如果原始问题不可解,它作为特定启发式算法的起点。
这里我们研究整数线性规划问题,其约束集合V是一个有理多面体约束,构成x的子集最少有一个整数约束;我们不区分纯整数规划和混合整数规划问题。
整数规划中最常用的松弛方法是对问题的连续性松弛,此时问题P的整数约束被忽略
拉格朗日松弛
下面介绍Held and Karp在1970和1971年提出的拉格朗日松弛(LR),不是一般性,假设如下问题:
![]()
引入一个非负的权重向量![]() ,即拉格朗日乘数,得到如下问题:
,即拉格朗日乘数,得到如下问题:
将问题的难约束放松并附加拉格朗日乘子作为目标函数的一部分,构成松弛问题。可知:松弛问题包含原始问题,任何![]() d都都小于或等于
d都都小于或等于![]() 。也就是说,对于所有的
。也就是说,对于所有的![]() ,
,![]() 的最优解是问题P最优解的下界。
的最优解是问题P最优解的下界。
综上,问题还可以转化为求问题P最紧的拉格朗日下界的对偶问题:
至此,在我们讨论拉格朗日松弛边界或简称朗格朗日边界时,我们通常指的是![]() 而非
而非![]() 。
。
假设我们考虑的复杂约束是等式而非不等式,则有如下问题:
将一个等式约束,通过两个朗格朗日乘子松驰为新的朗格朗日松弛问题,之后合并为并不要求![]() 为非负数的松弛问题
为非负数的松弛问题
可行的拉格朗日方案