数据结构——线性表

前提说明：整理的数据结构基本都是参考 大话数据结构这本书。

线性表的定义

• 线性表（List)：零个或多个数据元素的有限序列。

• 注意：
  1：它是一个序列
  2：有限的

• 判断方法：若元素存在多个，则第一个元素无前驱，最后一个元素无后继，其它每个元素都有且指由一前驱和后继。

线性表的抽象数据类型

ADT 线性表（List)
Data
…

Operation	_
InitList(*L)	初始化操作，建立一个空的线性表
ListEmpty(L)	若线性表为空，则返回 true， 否则返回 false
ClearList(*L)	将线性表清空
GetElem(L, i, e)	将线性表中第 i 个元素值返回给 e
LocatElem(L, e)	在线性表中查找与给定值e相等的元素，查找成功，返回序号，否则，返回0
ListInsert(*L, i, e)	在线性表第i个位置插入新元素 e
ListDelete(*L, i, *e)	删除线性表L中第i个位置的元素，并用e 返回其值
ListLength(L)	返回线性表L中元素的个数

endADT

线性表的顺序存储结构(即顺序表）

顺序存储定义：

用一段连续的存储单元一次存储线性表的数据元素

a1	a2	…	ai-1	ai	…	an

顺序存储方式

描述顺序存储结构的三个属性：

• 存储空间的起始位置:数组data 的存储位置就是存储空间的存储位置
• 线性表的最大存储量:数组长度MaxSize
• 线性表的当前长度：length

#define MAXSIZE 20
typedef int ElemType;
typedef struct
{
	ElemType data[MAXSIZE];
	int length;
}SqList;

**注意：**在任意时刻，线性表的长度 <= 数组长度

地址计算方法

何为地址： 存储器中每个存储单元都有自己的编号，这个编号称之为地址。
位置关系:

LOC(a_i+1) = LOC(a_i) + c
LOC(a_i) = LOC(a₁) + c*(i-1)

a1	a2	…	ai-1	ai	…	an	空闲位置
0	1		i-2	i-1	…	n-1

c 为存储单元

顺序存储结构的插入和删除

获得元素操作

/*
* 由于我是一边学习数据结构，一边整理
* 所以每一个代码，我都去展示完整的，主要是锻炼自己
* 将顺序表 L 中的第 i 个位置元素值返回
* 时间复杂度 O(1)
*/

#include 

#define MAXSIZE 30        // 顺序表的最大存储长度
#define OK 1
#define ERROR 0

typedef struct
{
	int data[MAXSIZE];  
	int length;          //   顺序表的长度
}SqList;

// 获取元素
int GetElem(SqList L, int i, int *e)
{
	if(L.length == 0 || i < 1 || i > L.length)    // 这里的判断要注意
		retuen ERROR;
	*e = L.data[i-1];
	return OK;
}

int main(void)
{
	SqList L;
	int i;
	int e;
	L.length = 10;       // 顺序表长度

// 在这里我想说一件特别搞笑的事，我关掉了 num lk 键，然后一直输入数字，输入失败，还跑去问了好多人
	for(i = 0; i < L.length; i ++)
		scanf("%d", &L.data[i]);         // 输入顺序表元素
	
	for(i = 0; i < L.length; i ++)
		printf("%d  ", L.data[i]);        // 输出顺序表元素
	printf("\n);

	printf("%d \n", GetElem(L, 3, &e));      // 这边之前有一个bug 但是我还没有找到原因
	printf("%d  \n", e);
	return 0;
}
	

插入操作

• 图示举例

插队前

1	2	3	4	5	6	7	空闲空间

person 插入到 3 号位置

1	2	person	3	4	5	6	7	空闲位置

则后边的人都需要后移

• 插入算法思路：

1：如果插入位置不合理，抛出异常
2：如果线性表长度大于数组长度，抛出异常或动态增加容量
3：从最后一个元素开始向前遍历到第 i 个位置，分别将他们都向后移动一个位置
4：将要插入元素填入位置 i
5：表长加 1

/*
* 若插入位置在最后一个位置，O(1);
* 其它位置，则为 O(n);
*/
#include 

#define OK 1
#define ERROR 0
#define MAXSIZE 30

typedef struct
{
	int data[MAXSIZE];
	int length;
}SqList;

int ListInsert (SqList *L, int i, int e)
{
	int k;
	if(L->length == MAXSIZE)			// 线性表已满
		return 	ERROR;
	if(i < 1 || i > L->length + 1)       // i 不在范围
		return ERROR;
	if(i < L->length)       // 不在表尾
	{
		for(k = L->length-1; k >= i-1; k --)
			L->data[k+1] = L->data[k];
	}
	L->data[i-1] = e;
	L->length ++;
	return OK;
}
int main(void)
{
	SqList *L;
	SqList sqList;
	L = &sqList;

	L->length = 10;
	for(i = 0; i < L->length; i ++)
		scanf("%d", &L->data[i]);
		
	for(i = 0; i < L->length; i ++)
		printf("%d  ", L->data[i]);
	printf("\n");
	
	printf("%d\n", ListInsert(L, 3, 11));
	printf("%d\n", L->length);    // 输出表长
	
	for(i = 0; i < L->length; i ++)
		printf("%d  ", L->data[i]);
	printf("\n");
	
	return 0;
}

删除操作

删除算法思路

• 如果删除位置不合理，抛出异常
• 取出删除元素
• 从删除元素位置开始遍历到最后一个元素位置，分别将它们都向前移一步
• 表长减1

/**
*若删除位置在最后一个位置，O(1);
* 其它位置，则为 O(n);
*/
#include 

#define MAXSIZE 30
#define OK 1
#define ERROR 0

typedef struct
{
	int data[MAXSIZE];
	int length;
}SeqList;

int ListDelete(SeqList *L, int i, int *e)
{
	int k;
	if(L->length == 0)
		return ERROR;
	if(i > L->length || i < 1)
		return ERROR;
	*e = L->data[i-1];
	if(i < L->length)
		for(k = i; k < L->length; k ++)
			L->data[k-1] = L->data[k];     // notice
	L->length --;
	return OK;
}
int main(void)
{
	int i;
    SqList *L;
	SqList sqList;
	int e;
	L = &sqList;

	L->length = 10;
	for(i = 0; i < L->length; i ++)
		scanf("%d", &L->data[i]);
		
	for(i = 0; i < L->length; i ++)
		printf("%d  ", L->data[i]);
	printf("\n");
	
	printf("%d\n", ListDelete(L, 3, &e));
	printf("%d\n", L->length); 
	printf("%d\n", e);
	for(i = 0; i < L->length; i ++)
		printf("%d  ", L->data[i]);
	printf("\n");
}

线性表顺序存储结构的优缺点

优点	缺点
可以快速的存取表中任何元素	插入和删除操作需要移动大量元素
无须为表示表中元素之间的逻辑关系而增加额外的存储空间	当线性表长度变化较大时，难以确定存储空间的容量
	造成存储空间“碎片”

线性表的链式存储结构（即链表）

注意几个名词： 数据域、指针域、结点、头指针、头结点
由于我正在熬夜赶这个，这些你们就在数中看着了解；其次，我的目的主要是复习代码以及算法思路。

单链表

单链表的存储结构

typedef struct Node
{
	int data;             // 数据域
	struct Node *next;        // 指针域
}Node;
typedef struct Node *LinkList;

单链表的读取

获得第 i 个元素的算法思路：

• 声明一个指针 p 指向链表的第一个节点
• 当 j < i 时， 就遍历链表，让 p 的指针向后移动，不断指向下一结点， j 累加1
• 若到链表末尾 p 为空，则说明第 i 个结点不存在
• 否则查找成功，则返回结点 p 的数据

#include 
#define OK 1
#define ERROR 0
typedef struct Node
{
	int data;
	struct Node *next;
}Node;
typedef struct Node *Linklist;

int GetElem(Linklist L, int i, int *e)
{
	int j;
	Linklist p;
	p = L->next;
	j = 1;
	
	while(p && j < i)
	{
		p = p->next;
		j ++;
	}
	if(!p || j > i)
		return ERROR;
	*e = p->data;
	return 	OK;
}

int main(void)
{
	Node a, b, c, d;
	Linklist L;
	int e;
	L = &a;
	a.data = 1;
	a.next = &b;
	b.data = 2;
	b.next = &c;
	c.data = 3;
	c.next = &d;
	d.data = 4;
	d.next = NULL;
	
	printf("%d\n", GetElem(L, 2, &e));
	printf("%d\n", e);
	return 0;
}

单链表的插入

单链表第 i 个数据插入结点的算法思路：

• 声明一个指针 p 指向链表头结点，初始化 j 从 1 开始
• 当 j < i 是，就便利链表，让 p 的指针向后移动，不断指向下一结点， j 累加 1
• 若到链表末尾 p 为空，则说明 第 i个结点不存在
• 否则查找成功，在系统中生成一个空结点 s
• 将数据元素 e 赋值给 s->data
• 单链表的插入标准语句 s->next = p->next, p = s->next
• 返回成功

/* 放弃敲完整代码，太累了*/
/*在L中的第i个结点位置之前插入新的数据元素 e ，L中长度 加 1*/
int ListInsert (LinkList L, int i, int e)
{
	int j;
	LinkList p, s;
	j = 1;
	p = *L;
	while(p && j < i)
	{
		p = p -> next;
		j ++;;
	}
	if(!p || j > i)
		return ERROR;
	
	s = (LinkList)malloc(sizeof(Node));    // 生成新结点
	s -> data = e;
	s -> next = p -> next;
	p -> next = s;
	return OK;
}
	

单链表删除

单链表第 i 个数据删除节点的算法思路：

• 声明一个指针 p 指向链表的头指针，初始化 j 从 1 开始
• 当 j < i 时，就遍历链表，让 p 的指针向 后 移动 ，不断指向下一个节点，j ++;
• 若到链表末尾 p 为空，则说明 第 i 个结点不存在
• 否则查找成功，将要删除的结点 p->next 赋值 q
• p->next = q -> next
• 将 q 结点中的数据赋值 给 e, 作为返回
• 释放 q 结点
• 返回成功

int ListDelete(LinkList L, int i, int *e)
{
	LinkList p, q;
	int j;
	p = L;
	j = 1;

	while(p-next && j < i)
	{
		p = p -> next;
		j ++;
	}
	if ( !(p->next) || j > i)
		return ERROR;
	
	q = p->next;
	p -> next = q -> next;
	*e = q -> data;
	free(q);
	return OK;
}

单链表整表创建

头插法

算法思路：

• 声明一个指针p和一个计数器 i
• 初始化一个空链表 L
• 让 L的头结点指向 NULL，即建立一个带头结点的空链表
• 循环：
  生成一个新结点赋值给 p
  随机生成 一个数字 赋值给 p 的数据域 p -> data
  将 p插入到 头结点与前以新结点之间

LinkList CreateListHead()
{
	LinkList L, p;
	int x;
	L = (LinkList)malloc(sizeof(Node));
	L->next = NULL;
	scanf("%d", &x);
	while ( x != -1)
	{
		p = (LinkList)malloc(sizeof(Node));
		p->data = x;
		p->next = L->next;
		L->next = p;
		scanf("%d", &x);
	}
	return L;
}
	

尾插法

LinkList CreateListTail()
{
	LinkList L, p, r;
	int x;
	L = (LinkList)malloc(sizeof(Node));
	r = L;
	scanf("%d", &x);
	while(x != -1)
	{
		p = (LinkList)malloc(sizeof(Node));
		p->data = x;
		r->next = p;
		r = p;
		scanf("%d", &x);
	}
	r->next = NULL;
	return L;
}

单链表整表删除

算法思路：

• 声明结点 p q
• 将第一个结点赋值给 p ,
• 循环：
  将下一节点赋值给 q
  释放 p
  将 q 赋值 给 p

int ClearList(LinkList L)
{
	LinkList p, q;
	p = L->next;
	while(p)
	{
		q = p->next;
		free(p);
		p = q;
	}
	L->next = NULL;
	return OK;
}

单链表与顺序存储结构比较

·	存储分配方式	时间性能	空间性能
顺序存储结构	一段连续的存储单元依次存储线性表的数据元素	查找：O(1) 插入删除O（n)	需要预分配存储空间，分多浪费；分少发生上溢
单链表	采用链式存储空间，任意的存储单元	查找O（n); 插入删除o（n)	不需要分配存储空间，有就可以分配，元素个数不受限
二者应优势互补

静态链表

• 用数组描述的链表称作静态链表
• 数组的元素由两个数据域组成，data 和 cur
• cur 存放该后继元素在数组中的下标位置
• 为方便插入数据，通常会把数组建立的大一些，以便有一些空闲空间可以便于插入时不至于溢出

/* 线性表的静态链表存储结构*/
#define MAXSIZE 10000
typedef struct
{
	int data;
	int cur;
}Component, StaticLinkList[MAXSIZE];

说明：数组的第一个元素（下标为0）的 cur 存放备用链表的第一个结点的下标；数组的最后一个元素的 cur 存放第一个有数值的元素的下标

int InitList(StaticLinkList space)
{
	int i;
	for(i = 0; i < MAXSIZE-1; i ++)
		space[i].cur = i + 1;
	space[MAXSIZE-1].cur = 0;
	return OK;
}

静态链表的插入

思路： 将所有未被使用过的及已被删除的分量用游标链成一个备用链表，每次进行插入时，从备用链表取得第一个结点作为待插入的新结点

/* 若备用链表为非空，则返货分配的结点的下标，否则返回0*/
int Malloc_SLL(StaticLinkList space)
{
	int i = space[0].cur;   // 返回第一个备用空间的下标
	if(space[0].cur)
		space[0].cur = space[i].cur;   // 更换备用链表的下标
	return i;
}

/* 在L中 第 i 个元素之前插入元素 e */
int ListInsert(StaticLinkList L, int i, int e)
{
	int j, k, l;         //  K 为最后一个元素的下标（即存放第一个元素位置的下标）
	if(i < 1 || i > ListLength(L) + 1)
		return ERROR;
	j = Malloc_SLL(L);  // 分配的空间的下标
	if(j)
	{
		L[j].data = e;
		for(l = 1; l < i; l ++)
			k = L[k].cur;
		L[j].cur = L[k].cur;
		L[k].cur = j;
		return OK;
	}
	return ERROR;
}
	

静态链表的删除

/* 将下标为 k 的空闲节点回收到备用链表*/
void Free_SLL(StaticLinkList space, int k)
{
	space[k].cur = space[0].cur;
	space[0].cur = k;
}

/* 删除 L 中的第 i个元素e */
int ListDelete(StaticLinkList L, int i)
{
	int j, k;
	k = MAXSIZE -1;
	if(i < 1 || i > ListLength(L) + 1)
		return ERROR;
	for(j = 1; j < i; j ++)
		k = L[k].cur;
	j = L[k].cur;
	L[k].cur = L[j].cur;
	Free_SLL(L, j);
	return OK;
}

/* 返回L中的数据元素个数*/
int ListLength(StaticLinkList L)
{
	int j = 0;
	int i = L[MAXSIZE-1].cur;
	while(i)
	{
		i = L[i].cur;
		j ++;
	}
	return j;
}

静态链表优缺点

优点	缺点
插入和删除时只需要修改游标，不需要移动元素	没有解决连续存储分配带来的表长难以确定的我问题；失去了顺序存储结构随机存取的特性

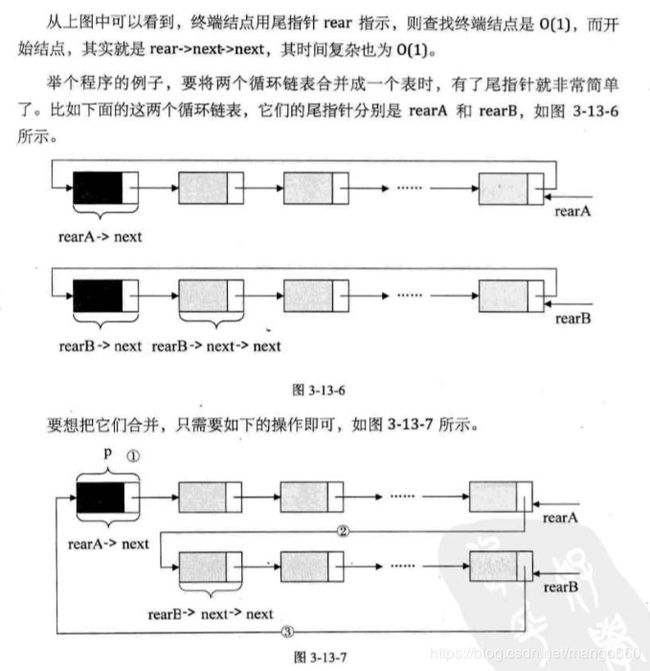
循环链表

p = rearA->next;
rearA->next = rearB->next->next;
q = rearB->next;
rearB->next = p;
free(q);

双向链表

/*双向链表的存储结构*/
typedef struct DuLNode
{
	int data;
	struct DuLNode *prior;
	struct DuLNode *next;
}DuLNode, *DuLinkList;

双向链表的许多操作与单链表相同

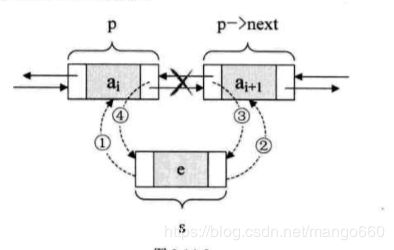
双向链表的插入操作

/* 插入操作 */ 
s->prior = p;
s->next = p->next;
p->next->prior = s;
p->nezt = s;

双向链表的删除操作

p->prior->next = p->next;
p->next->prior = p->prior;

对于这篇数据结构——线性表整理不到位的地方在整本书学完后会进行修改，这遍主要进行了算法思想以及代码展示，详细的知识点并未介绍。