AVL平衡树及插入操作的C语言实现

源码地址：http://download.csdn.net/detail/mcu_tian/9555855

AVL平衡二叉树是一种特殊的查找树，是一种每个节点的左右子树深度不超过1。

AVL是绝对平衡树，增删的操作复杂度过高，应用不如红黑树。

AVL树的引入，就是为了解决二叉查找树的不平衡性导致时间复杂度大大下降。

那么AVL就保持住了(BST)的最好时间复杂度O(logn)，所以每次的插入和删除都要确保二叉树的平衡。

在对AVL平衡树的插入和删除操作的过程中，有可能会破坏AVL树的特性，此时就要通过旋转操作将插入节点的树恢复为AVL树。

AVL节点结构定义

AVL的节点结构定义与查找树基本上相同，不同在于增加了height成员，用来保存以该节点为根的子树的深度。

struct AvlNode
{
    ElementType element;
    struct AvlNode *left;
    struct AvlNode *right;

    int frequency;
    int heigh;
};
typedef struct AvlNode *NodePtr;
typedef struct AvlNode *AvlTree;
typedef struct AvlNode Node;

AVL插入操作

就插入操作而言

在插入操作以后，只有那些从插入点到根节点的路径上的节点的平衡关系可能被改变，因为只有这些节点的子树可能发生变化。

因此我们可以沿着这条路径上行到根并更新平衡信息时，我们可以找到一个平衡节点，该节点子树旋转重新平衡后，新平衡保证了整个树满足AVL特性。

需要重新平衡的节点为路径中检测到左右子树的深度相差超过2的最接近插入节点的节点。

需要重新平衡的节点。插入后，该平衡节点出现不平衡的情况有四种

1：在该节点的左儿子的左子树进行一次插入操作

2：在该节点的右儿子的右子树进行一次插入操作

3：在该节点的左儿子的右子树进行一次插入操作

4：在该节点的右儿子的左子树进行一次插入操作

在对1和2这两种情况只需要进行单旋转

对3和4这两种情况需要进行双旋转

具体如图，红色填充节点为插入节点：

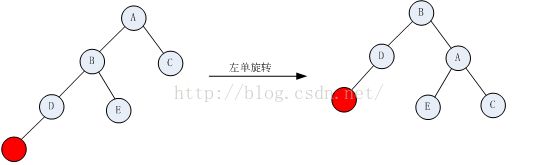
第一种情况：

需要对其进行左单旋转，将B提升为根节点，A的左子树为替换为B的右子树，A节点为B节点的右孩子

左单旋转其C实现如下：

AvlTree SingleRotateLeft(AvlTree t)//左单旋转
{
       NodePtr tmp = t->left;

       t->left = tmp->right;
       tmp->right = t;

       t->heigh = MAX(Heigh(t->left),Heigh(t->right))+1;//更新子树节点深度
       tmp->heigh = MAX(Heigh(tmp->left),Heigh(tmp->right))+1;

       return tmp;
}

第二种情况：

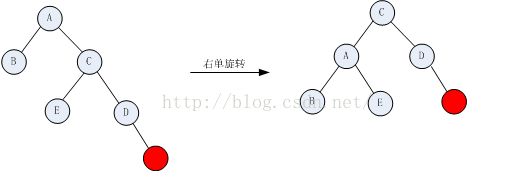
该种情况需要对该树进行右旋转，该操作将C节点提升为根节点，同时将节点C的左节点作为节点A的右子树，A成为C的左孩子。

右单旋转的操作C语言实现如下：

AvlTree SingleRotateRight(AvlTree t)
{
    NodePtr tmp = t->right;

    t->right = tmp->left;
    tmp->left = t;

    t->heigh = MAX(Heigh(t->left),Heigh(t->right))+1;
    tmp->heigh = MAX(Heigh(tmp->left),Heigh(tmp->right))+1;

    return tmp;
}

第三种情况：

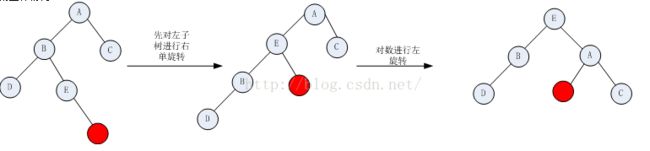
该种情况，单旋转的操作不能实现新平衡，先对左子树进行右旋转，旋转之后，然后再进行左旋转

右-左双旋转的操作C语言实现

AvlTree DoubleRotateLeft(AvlTree t)
{
    t->left = SingleRotateRight(t->left);//先右再左
    t = SingleRotateLeft(t);
    return t;
}

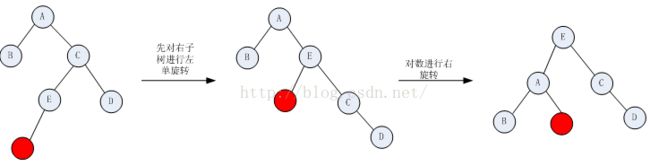
第四种情况如下:

该种情况，单旋转的操作不能实现新平衡，先对右子树进行左旋转，旋转之后，然后再进行右旋转

左-右双旋转的操作C语言实现

AvlTree doubleRotateRight(AvlTree t)
{
   t->right = SingleRotateLeft(t->right);//先左再右
   t = SingleRotateRight(t);
   return t;
}

在搞定旋转实现新平衡之后，那就实现了AVL插入、删除操作的最最关键部分

插入操作Insert

插入操作的实现用递归的方法C语言实现：

AvlTree Insert(ElementType element, AvlTree t)
{
    if(t == NULL)
    {
        t = MallocAvlNode(element); //节点插入位置
        if(t == NULL)
        {
            printf("malloc avl node failed\n");
            return t;
        }
    }
    else if(element < t->element)
    {
        t->left = Insert(element,t->left); //插入元素小于节点元素则插入左子树中
        if(Heigh(t->left) - Heigh(t->right) == 2)
        {
            if(element < t->left->element) //为第一种情况
            {
                t = SingleRotateLeft(t);
            }
            else
            {
               t=  DoubleRotateLeft(t);//第三种情况
            }
        }

    }
    else if(element > t->element)  //若是大于则插入右子树
    {
        t->right = Insert(element,t->right);
        if(Heigh(t->right) - Heigh(t->left) >= 2)
        {
            if(element > t->element) //第二种情况
            {
                t = SingleRotateRight(t);
            }
            else
            {
                t = doubleRotateRight(t);//第四种情况
            }
        }
    }
    else  //若是相等，更行节点结构中frequency，进行加1
    {
        ++t->frequency;
    }
   t->heigh = MAX(Heigh(t->left),Heigh(t->right))+1; //更新节点的heigh成员
   return t;
}

删除操作中：

AVL节点的删除跟查找树思路是一样的，参考：http://blog.csdn.net/mcu_tian/article/details/51668883

删除节点之后，检查AVL的平衡性，若是AVL平衡性遭到破坏，则要建立新的平衡，进行旋转操作，与insert类似，但是判断时那种不平衡的情况不同。

测试

测试代码如下:

AvlTree t = NULL;

int main(void)
{
    int a[20] = {30,22,15,233,45,64,23,674,43,46,13,76,71,74,654,63,41,66,2,155};//测试数组
    int i;
    for(i = 0;i < 20;++i)
    {
        t = Insert(a[i],t);
    }
   PrintAvlTreeInorder(t);//中序打印AVL树，若是插入成功，则会从小到大的顺序依次打印插入的节点
   return 0;
}

测试结果如下，符合预期：