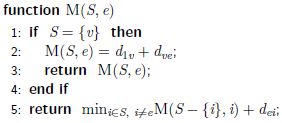计算机算法设计与分析一

对待问题的思路：

1、如果问题能分解成子问题，考虑分治，并且能观察最优子结构，考虑动态规划，如果问题有贪心性质，考虑贪心。

2、如果问题不能分或者不好分成问题，考虑逐步改进的方法，如线性规划，非线性规划，二次规划，网络流等。

3、观察解形式，x=[x1,x2,x3,x4...xn] xi=0/1，考虑枚举，智能枚举，贪心等。

4、对于hard问题，考虑放松标准，如最优解->近似解，确定性算法->随机的算法，最坏的情况下->正常的情况下。

实例一：

输入：两个数a,b（a>=b）

输出：gcd（a,b）

分析：可以分解成子问题，如gcd(1949,101)->gcd(101,30)->gcd(30,11)->gcd(11,8)->gcd(8,3)->gcd(3,2)->gcd(2,1)->gcd(1,0)，故采用分治算法。

代码：

function Euclid(a,b):
    if b=0 then
        return a;
    end if
    return Euclid(b,a mod b);

实例二：

输入：n个城市V=｛1，2，...，n｝，和一个距离矩阵D，dij（1<=i,j<=n）表示距离城市i到城市j。
输出：最短的旅程，游遍每个城市一次，回到最初的城市。

1、首先看能否分解成子问题

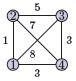
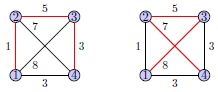
考虑M(S,e)表示最小距离，从城市1开始，旅行S中的每一个城市，并且最后到达e城市。

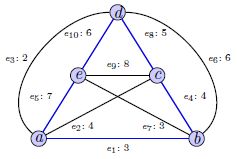
如下图：

最短路径可计算为:

min{d2,1 + M({3, 4}, 2),

d3,1 + M({2, 4}, 3),

d4,1 + M({2, 3}, 4)}

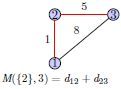
而如 M({2, 3},4)=min{d34 + M({2}, 3), d24 + M({3}, 2)}

而如M({2}, 3)=d12+d23

所以可以被分解成子问题

代码：

这里e是指V中除去1的每个点

这里i是指S中除去e的每个点

2、逐步改进策略

从一个粗略的完整的解决方案开始，然后逐步改进

这里stopping(s)是指已经没有neighbourhood可选了。

3、智能枚举策略

方法一：通过边

如上图，a → b → c → d → e → a可以表示为 X = [1, 0, 0, 1, 1, 0, 0, 1, 0, 1]

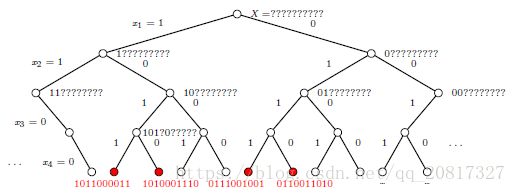
我们可以遍历所有的可能，如下图：

但是这样遍历的可能性太多了，效率太低，我们可以考虑用剪枝的方法来提高效率

方法：

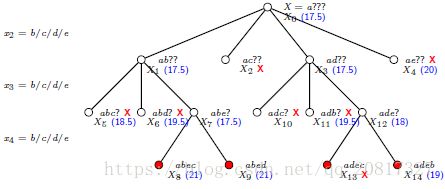
对于一个解X=？？？？？？？？，我们估计最短路程如下：

• 对于每个城市，我们选择最短的两条边
• 这两条边的和小于等于2倍的最优路程。
• 因此，我们可以给一个最低下界为1/2*(5+6+8+7+9)=17.5

如：对于X=10????????下界为1/2*(5+6+9+7+9)=18

所以，以此剪枝为

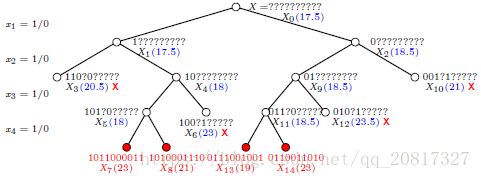
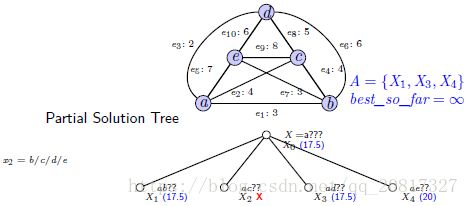
方法二：通过点

路程可以表示成点的序列，如X=[x1,x2,...,xn-1],xi为点，不失一般性，我们假定x1=a，且a,b在c之前出现。

于是我们可以这样展开：

最后，结果如下：