Spark大数据分布式图计算处理实战

​前言

    Spark是一种大规模、快速计算的集群平台，本公众号试图通过学习Spark官网的实战演练笔记提升笔者实操能力以及展现Spark的精彩之处。有关框架介绍和环境配置可以参考以下内容：    

    大数据处理框架Hadoop、Spark介绍

    linux下Hadoop安装与环境配置

    linux下Spark安装与环境配置

 

    本文的参考配置为：Deepin 15.11、Java 1.8.0_241、Hadoop 2.10.0、Spark 2.4.4、scala 2.11.12

    本文的目录为：

        一、属性图

            1.图计算入门

            2.属性图示例

        二、图运算符

            1.运算符列表

            2.属性运算符

            3.结构运算符

            4.Join运算符

            5.邻域聚合

        三、Pregel API

        四、图算法

            1.PageRank

            2.连接组件

            3.Triangle计数

 

一、属性图

    GraphX是Spark中用于图形和图形并行计算的新组件。在较高的层次上，GraphX 通过引入新的Graph抽象来扩展Spark RDD：一个有向多重图，其属性附加到每个顶点和边上。为了支持图计算，GraphX公开了一组基本的操作符（例如，子图、joinVertices和aggregateMessages），以及优化的Pregel API。此外，GraphX包括越来越多的图形算法和构建器集合，以简化图形分析任务。

    1.图计算入门

    首先，首先需要将Spark和GraphX导入项目，如下所示：

import org.apache.spark._import org.apache.spark.graphx._// 图计算也需要RDDimport org.apache.spark.rdd.RDD

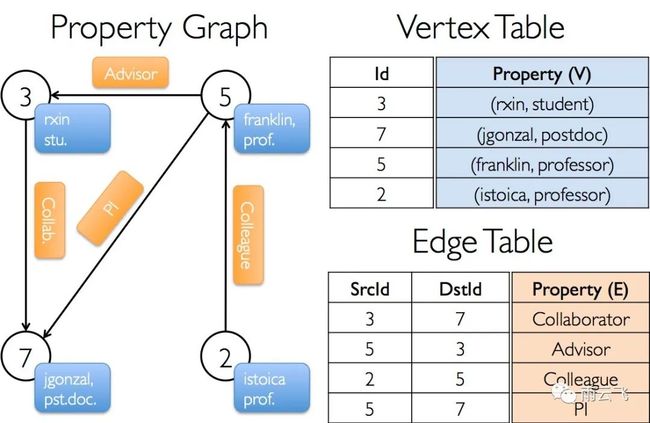
    属性图是一个定向多重图形，用户定义的对象附加到每个顶点和边缘。定向多图是具有共享相同源和目标顶点的潜在多个平行边缘的有向图。支持平行边缘的能力简化了在相同顶点之间可以有多个关系（例如：同事和朋友）的建模场景。每个顶点都由唯一的 64 位长标识符（VertexId）键入。GraphX 不对顶点标识符施加任何排序约束。类似地，边缘具有对应的源和目标顶点标识符。

    属性图是通过 vertex（VD）和 edge（ED）类型进行参数化的。这些是分别与每个顶点和边缘相关联的对象的类型。

    在某些情况下，可能希望在同一个图形中具有不同属性类型的顶点。这可以通过继承来实现。例如，将用户和产品建模为二分图，我们可能会执行以下操作：

scala> class VertexProperty()defined class VertexProperty​scala> case class UserProperty(val name: String) extends VertexPropertydefined class UserProperty​scala> case class ProductProperty(val name: String, val price: Double) extends VertexPropertydefined class ProductProperty​scala> var graph: Graph[VertexProperty, String] = nullgraph: org.apache.spark.graphx.Graph[VertexProperty,String] = null

    像 RDD 一样，属性图是不可变的，分布式的和容错的。通过生成具有所需更改的新图形来完成对图表的值或结构的更改。请注意，原始图形的大部分（即，未受影响的结构，属性和索引）在新图表中重复使用，可降低此内在功能数据结构的成本。使用一系列顶点分割启发式方法，在执行器之间划分图形。与 RDD 一样，在发生故障的情况下，可以在不同的机器上重新创建图形的每个分区。

    逻辑上，属性图对应于一对编码每个顶点和边缘的属性的类型集合（RDD）。因此，图类包含访问图形顶点和边的成员：

class Graph[VD, ED] {  val vertices: VertexRDD[VD]  val edges: EdgeRDD[ED]}

    VertexRDD[VD]和EdgeRDD[ED]分别扩展了RDD[(VertexId, VD)] 和 RDD[Edge[ED]] 的优化版本。VertexRDD[VD] 和 EdgeRDD[ED] 都提供了围绕图计算和利用内部优化的附加功能。

    2.属性图示例

    假设我们要构建一个由 GraphX 项目中的各种协作者组成的属性图。顶点属性可能包含用户名和职业。我们可以用描述协作者之间关系的字符串来注释边：

    从原始文件合成生成器构建属性图有许多方法，这些在图形构建器的一节中有更详细的讨论。最普遍的方法是使用Graph对象。例如，以下代码从RDD集合中构建一个图：

// 定义顶点scala> val Buildings: RDD[(VertexId, (String, String))] =     |   sc.parallelize(Array((3L, ("中南楼", "行政楼")), (7L, ("文泰楼", "教学楼")),     |                         (5L, ("中原楼", "行政楼")), (2L, ("文波楼", "行政楼"))))Buildings: org.apache.spark.rdd.RDD[(org.apache.spark.graphx.VertexId, (String, String))] = ParallelCollectionRDD[28] at parallelize at :32// 定义边scala> val relationships: RDD[Edge[String]] =     |   sc.parallelize(Array(Edge(3L, 7L, "不同校区不同性质"),    Edge(5L, 3L, "不同校区同性质"),     |                        Edge(2L, 5L, "同校区不同性质"), Edge(5L, 7L, "同校区不同性质")))relationships: org.apache.spark.rdd.RDD[org.apache.spark.graphx.Edge[String]] = ParallelCollectionRDD[29] at parallelize at :32// 定义默认楼栋scala> val defaultBuilding = ("文添楼", "教学楼")defaultBuilding: (String, String) = (文添楼,教学楼)// 初始化图scala> val graph = Graph(Buildings, relationships, defaultBuilding)graph: org.apache.spark.graphx.Graph[(String, String),String] = org.apache.spark.graphx.impl.GraphImpl@6ec5e204

    我们可以分别使用 graph.vertices 和 graph.edges 成员将图形解构成相应的顶点和边缘视图。

scala> graph.vertices.filter { case (id, (name, pos)) => pos == "行政楼" }.countres7: Long = 3​scala> graph.edges.filter(e => e.srcId > e.dstId).countres8: Long = 1

    除了属性图的顶点和边缘视图之外，GraphX 还暴露了三元组视图。三元组在视图逻辑上连接顶点和边缘属性，生成 RDD[EdgeTriplet[VD, ED]] 包含 EdgeTriplet 该类的实例。EdgeTriplet 类通过分别添加包含源和目标属性的 srcAttr 和 dstAttr 成员来扩展 Edge 类。我们可以使用图形的三元组视图来渲染描述用户之间关系的字符串集合。

scala> val facts: RDD[String] = graph.triplets.map(triplet => triplet.srcAttr._1 + " 与 " + triplet.dstAttr._1+ " 是 " + triplet.attr + "的楼")facts: org.apache.spark.rdd.RDD[String] = MapPartitionsRDD[26] at map at :32​scala> facts.collect.foreach(println(_))中南楼 与 文泰楼 是 不同校区不同性质的楼中原楼 与 中南楼 是 不同校区同性质的楼文波楼 与 中原楼 是 同校区不同性质的楼中原楼 与 文泰楼 是 同校区不同性质的楼

二、图运算符

    1.运算符列表

    以下是两个定义的功能的简要摘要，但为简单起见将Graph，GraphOps 作为 Graph 的成员呈现。

// 属性图中的函数总结class Graph[VD, ED] {  // 图的基本信息变量  val numEdges: Long  val numVertices: Long  val inDegrees: VertexRDD[Int]  val outDegrees: VertexRDD[Int]  val degrees: VertexRDD[Int]  // 图的集合  val vertices: VertexRDD[VD]  val edges: EdgeRDD[ED]  val triplets: RDD[EdgeTriplet[VD, ED]]  // 有关缓存的函数  def persist(newLevel: StorageLevel = StorageLevel.MEMORY_ONLY): Graph[VD, ED]  def cache(): Graph[VD, ED]  def unpersistVertices(blocking: Boolean = true): Graph[VD, ED]  // 改变分区方式  def partitionBy(partitionStrategy: PartitionStrategy): Graph[VD, ED]  // 转换顶点和边属性  def mapVertices[VD2](map: (VertexId, VD) => VD2): Graph[VD2, ED]  def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]  def mapEdges[ED2](map: (PartitionID, Iterator[Edge[ED]]) => Iterator[ED2]): Graph[VD, ED2]  def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]  def mapTriplets[ED2](map: (PartitionID, Iterator[EdgeTriplet[VD, ED]]) => Iterator[ED2])    : Graph[VD, ED2]  // 修改图结构  def reverse: Graph[VD, ED]  def subgraph(      epred: EdgeTriplet[VD,ED] => Boolean = (x => true),      vpred: (VertexId, VD) => Boolean = ((v, d) => true))    : Graph[VD, ED]  def mask[VD2, ED2](other: Graph[VD2, ED2]): Graph[VD, ED]  def groupEdges(merge: (ED, ED) => ED): Graph[VD, ED]  // 连接RDD和图  def joinVertices[U](table: RDD[(VertexId, U)])(mapFunc: (VertexId, VD, U) => VD): Graph[VD, ED]  def outerJoinVertices[U, VD2](other: RDD[(VertexId, U)])      (mapFunc: (VertexId, VD, Option[U]) => VD2)    : Graph[VD2, ED]  // 汇总有关相邻三元组的信息   def collectNeighborIds(edgeDirection: EdgeDirection): VertexRDD[Array[VertexId]]  def collectNeighbors(edgeDirection: EdgeDirection): VertexRDD[Array[(VertexId, VD)]]  def aggregateMessages[Msg: ClassTag](      sendMsg: EdgeContext[VD, ED, Msg] => Unit,      mergeMsg: (Msg, Msg) => Msg,      tripletFields: TripletFields = TripletFields.All)    : VertexRDD[A]  // 迭代图遍历计算   def pregel[A](initialMsg: A, maxIterations: Int, activeDirection: EdgeDirection)(      vprog: (VertexId, VD, A) => VD,      sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId,A)],      mergeMsg: (A, A) => A)    : Graph[VD, ED]  // 基本的图算法  def pageRank(tol: Double, resetProb: Double = 0.15): Graph[Double, Double]  def connectedComponents(): Graph[VertexId, ED]  def triangleCount(): Graph[Int, ED]  def stronglyConnectedComponents(numIter: Int): Graph[VertexId, ED]}

    2.属性运算符

    与 RDD map 运算符一样，属性图包含以下内容：

class Graph[VD, ED] {  def mapVertices[VD2](map: (VertexId, VD) => VD2): Graph[VD2, ED]  def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]  def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]}

    这些运算符中的每一个都会产生一个新图形，该图形的顶点或边属性由用户定义的map函数修改。

    3.结构运算符

    目前GraphX只支持一套简单的常用结构运算符，我们预计将来会增加更多。以下是基本结构运算符的列表。

class Graph[VD, ED] {  def reverse: Graph[VD, ED]  def subgraph(epred: EdgeTriplet[VD,ED] => Boolean,               vpred: (VertexId, VD) => Boolean): Graph[VD, ED]  def mask[VD2, ED2](other: Graph[VD2, ED2]): Graph[VD, ED]  def groupEdges(merge: (ED, ED) => ED): Graph[VD,ED]}

• 该 reverse 运算符将返回逆转的所有边缘方向上的新图。这在例如尝试计算逆 PageRank 时是有用的。由于反向操作不会修改顶点或边缘属性或更改边缘数量，因此可以在没有数据移动或重复的情况下高效地实现。

• 在 subgraph 操作者需要的顶点和边缘的谓词，并返回包含只有满足谓词顶点的顶点的曲线图（评估为真），并且满足谓词边缘边缘 _并连接满足顶点谓词顶点_。所述 subgraph 操作员可在情况编号被用来限制图形以顶点和感兴趣的边缘或消除断开的链接。

• 在 mask 操作者通过返回包含该顶点和边，它们也在输入图形中发现的曲线构造一个子图。这可以与 subgraph 运算符一起使用，以便根据另一个相关图中的属性限制图形。例如，我们可以使用缺少顶点的图运行连接的组件，然后将答案限制为有效的子图。

• groupEdges 操作符将多边形中的平行边（即，顶点对之间的重复边）合并。在许多数值应用中，可以将平行边缘（它们的权重组合）合并成单个边缘，从而减小图形的大小。

    4.Join运算符

    在许多情况下，有必要使用图形连接来自外部收集（RDD）的数据。例如，我们可能有额外的用户属性，我们要与现有的图形合并，或者我们可能希望将顶点属性从一个图形拉到另一个。这些任务可以使用 join 运算符完成。下面我们列出关键 join 运算符：

class Graph[VD, ED] {  def joinVertices[U](table: RDD[(VertexId, U)])(map: (VertexId, VD, U) => VD)    : Graph[VD, ED]  def outerJoinVertices[U, VD2](table: RDD[(VertexId, U)])(map: (VertexId, VD, Option[U]) => VD2)    : Graph[VD2, ED]}

• joinVertices 操作符将顶点与输入 RDD 相连，并返回一个新的图形，其中通过将用户定义的 map 函数应用于已连接顶点的结果而获得的顶点属性。RDD 中没有匹配值的顶点保留其原始值。

• 除了将用户定义的 map 函数应用于所有顶点并且可以更改顶点属性类型之外，更一般的 outerJoinVertices 的行为类似于 joinVertices。因为不是所有的顶点都可能在输入 RDD 中具有匹配的值，所以 map 函数采用 Option 类型。

    5.邻域聚合

    许多图形分析任务的关键步骤是聚合关于每个顶点邻域的信息。例如，我们可能想知道每个用户拥有的关注者数量或每个用户的追随者的平均年龄。许多迭代图表算法（例如：网页级别，最短路径，以及连接成分）相邻顶点（例如：电流值的 PageRank，最短到源路径，和最小可达顶点 ID）的重复聚合性质。

    GraphX 中的核心聚合操作是 aggregateMessages（聚合消息）。该运算符将用户定义的 sendMsg 函数应用于图中的每个 边缘三元组，然后使用该 mergeMsg 函数在其目标顶点聚合这些消息。

class Graph[VD, ED] {  def aggregateMessages[Msg: ClassTag](      sendMsg: EdgeContext[VD, ED, Msg] => Unit,      mergeMsg: (Msg, Msg) => Msg,      tripletFields: TripletFields = TripletFields.All)    : VertexRDD[Msg]}

    用户定义的 sendMsg 函数接受一个 EdgeContext，它将源和目标属性以及 edge 属性和函数 (sendToSrc和 sendToDst) 一起发送到源和目标属性。在 map-reduce 中，将 sendMsg 作为 map 函数。用户定义的 mergeMsg 函数需要两个发往同一顶点的消息，并产生一条消息。想想 mergeMsg 是 map-reduce 中的 reduce 函数。aggregateMessages 运算符返回一个 VertexRDD[Msg]，其中包含去往每个顶点的聚合消息（Msg类型）。没有收到消息的顶点不包括在返回的 VertexRDDVertexRDD 中。

三、Pregel API

    图形是固有的递归数据结构，因为顶点的属性取决于其邻居的属性，而邻居的属性又依赖于 其 邻居的属性。因此，许多重要的图算法迭代地重新计算每个顶点的属性，直到达到一个固定点条件。已经提出了一系列图并行抽象来表达这些迭代算法。GraphX 公开了 Pregel API 的变体。在以下示例中，我们可以使用 Pregel 运算符来表达单源最短路径的计算：

import org.apache.spark.graphx.{Graph, VertexId}import org.apache.spark.graphx.util.GraphGenerators​// 带有包含距离属性的边的图scala> val graph: Graph[Long, Double] = GraphGenerators.logNormalGraph(sc, numVertices = 100).mapEdges(e => e.attr.toDouble)graph: org.apache.spark.graphx.Graph[Long,Double] = org.apache.spark.graphx.impl.GraphImpl@6fdc624val sourceId: VertexId = 42 // 最终来源// 初始化图scala> val initialGraph = graph.mapVertices((id, _) => if (id == sourceId) 0.0 else Double.PositiveInfinity)initialGraph: org.apache.spark.graphx.Graph[Double,Double] = org.apache.spark.graphx.impl.GraphImpl@211d223f​scala> val sssp = initialGraph.pregel(Double.PositiveInfinity)(     |   (id, dist, newDist) => math.min(dist, newDist), // 顶点程序     |   triplet => {  // 发送消息     |     if (triplet.srcAttr + triplet.attr < triplet.dstAttr) {     |       Iterator((triplet.dstId, triplet.srcAttr + triplet.attr))     |     } else {     |       Iterator.empty     |     }     |   },     |   (a, b) => math.min(a, b) // 合并消息     | )sssp: org.apache.spark.graphx.Graph[Double,Double] = org.apache.spark.graphx.impl.GraphImpl@5be47769​scala> println(sssp.vertices.collect.mkString("\n"))(84,1.0)(96,2.0)... ... ...

四、图算法

    GraphX 包括一组简化分析任务的图算法。该算法被包含在 org.apache.spark.graphx.lib 包可直接作为方法通过 GraphOps来访问 Graph。本节介绍算法及其使用方法。

    1.PageRank

    PageRank 测量在图中每个顶点的重要性，假设从边缘 u 到 v 表示的认可 v 通过的重要性 u。例如，如果 Twitter 用户遵循许多其他用户，则用户将被高度排名。

    GraphX 附带了 PageRank 的静态和动态实现方法作PageRank 对象上的方法。静态 PageRank 运行固定次数的迭代，而动态 PageRank 运行直到排列收敛（即，停止改变超过指定的公差）。GraphOps 允许直接调用这些算法作为方法 Graph。

    GraphX还包括一个可以运行 PageRank 的社交网络数据集示例。给出了一组用户data/graphx/users.txt，并给出了一组用户之间的关系 data/graphx/followers.txt。我们计算每个用户的 PageRank 如下：

import org.apache.spark.graphx.GraphLoader​scala> val Graph = GraphLoader.edgeListFile(sc,"file:///usr/local/spark/data/graphx/followers.txt")Graph: org.apache.spark.graphx.Graph[Int,Int] = org.apache.spark.graphx.impl.GraphImpl@4b05a635​scala> val ranks = graph.pageRank(0.0001).verticesranks: org.apache.spark.graphx.VertexRDD[Double] = VertexRDDImpl[954] at RDD at VertexRDD.scala:57​scala> val users = sc.textFile("data/graphx/users.txt").map { line =>     |   val fields = line.split(",")     |   (fields(0).toLong, fields(1))     | }users: org.apache.spark.rdd.RDD[(Long, String)] = MapPartitionsRDD[963] at map at :34​scala> val users = sc.textFile("file:///usr/local/spark/data/graphx/users.txt").map { line =>     | val fields = line.split(",")     | (fields(0).toLong, fields(1))     | }users: org.apache.spark.rdd.RDD[(Long, String)] = MapPartitionsRDD[966] at map at :34​scala> val ranksByUsername = users.join(ranks).map {     |   case (id, (username, rank)) => (username, rank)     | }ranksByUsername: org.apache.spark.rdd.RDD[(String, Double)] = MapPartitionsRDD[970] at map at :37​scala> println(ranksByUsername.collect().mkString("\n"))(justinbieber,1.1572302808266979)(anonsys,1.3213594965245234)(BarackObama,1.0873678421339295)(matei_zaharia,1.0399824275230816)(ladygaga,0.8845423166697186)(jeresig,1.150821600247031)(odersky,1.2192581719573445)

    2.连接组件

连接的组件算法将图中每个连接的组件与其最低编号顶点的ID进行标记。例如，在社交网络中，连接的组件可以近似群集。GraphX包含ConnectedComponents object 中算法的实现，我们从PageRank 部分计算示例社交网络数据集的连接组件如下：

import org.apache.spark.graphx.GraphLoader// 加载PageRank官方示例文件scala> val Graph = GraphLoader.edgeListFile(sc,"file:///usr/local/spark/data/graphx/followers.txt")Graph: org.apache.spark.graphx.Graph[Int,Int] = org.apache.spark.graphx.impl.GraphImpl@49a28c9e// 查找连接组件scala> val cc = graph.connectedComponents().verticescc: org.apache.spark.graphx.VertexRDD[org.apache.spark.graphx.VertexId] = VertexRDDImpl[1021] at RDD at VertexRDD.scala:57//  与带有用户名的连接组件Jionscala> sc.textFile("file:///usr/local/spark/data/graphx/users.txt").collect()res16: Array[String] = Array(1,BarackObama,Barack Obama, 2,ladygaga,Goddess of Love, 3,jeresig,John Resig, 4,justinbieber,Justin Bieber, 6,matei_zaharia,Matei Zaharia, 7,odersky,Martin Odersky, 8,anonsys)scala> val users = sc.textFile("file:///usr/local/spark/data/graphx/users.txt").map {line =>      | val fields = line.split(",")     | (fields(0).toLong, fields(1))     | }users: org.apache.spark.rdd.RDD[(Long, String)] = MapPartitionsRDD[1049] at map at :36scala> val ccByUsername = users.join(cc).map {     | case (id, (username, cc)) => (username, cc)     | }ccByUsername: org.apache.spark.rdd.RDD[(String, org.apache.spark.graphx.VertexId)] = MapPartitionsRDD[1053] at map at :39// 输出结果scala> println(ccByUsername.collect().mkString("\n"))(justinbieber,0)(anonsys,0)(BarackObama,0)(matei_zaharia,0)(ladygaga,0)(jeresig,0)(odersky,0)

    3.Triangle计数

    顶点是三角形的一部分，当它有两个相邻的顶点之间有一个边。GraphX 在 TriangleCount 对象中实现一个三角计数算法，用于确定通过每个顶点的三角形数量，提供聚类度量。我们从PageRank 部分计算社交网络数据集的三角形数。需要注意的是 TriangleCount 边缘要处于规范方向（srcId & dstId），而图形要使用 Graph.partitionBy。

import org.apache.spark.graphx.{GraphLoader, PartitionStrategy}// 以规范顺序加载边线并划分图形以进行三角形计数scala> val graph = GraphLoader.edgeListFile(sc, "file:///usr/local/spark/data/graphx/followers.txt", true)graph: org.apache.spark.graphx.Graph[Int,Int] = org.apache.spark.graphx.impl.GraphImpl@71efa96c​scala> val graph = GraphLoader.edgeListFile(sc, "file:///usr/local/spark/data/graphx/followers.txt", true).partitionBy(PartitionStrategy.RandomVertexCut)graph: org.apache.spark.graphx.Graph[Int,Int] = org.apache.spark.graphx.impl.GraphImpl@21f8fee3// 找到每个顶点的三角形数scala> val triCounts = graph.triangleCount().verticestriCounts: org.apache.spark.graphx.VertexRDD[Int] = VertexRDDImpl[1134] at RDD at VertexRDD.scala:57// 使用用户名Join三角形数scala> val users = sc.textFile("file:///usr/local/spark/data/graphx/users.txt").map { line =>     | val fields = line.split(",")     | (fields(0).toLong, fields(1))     | }users: org.apache.spark.rdd.RDD[(Long, String)] = MapPartitionsRDD[1139] at map at :38​scala> val triCountByUsername = users.join(triCounts).map { case (id, (username, tc)) => (username, tc)}triCountByUsername: org.apache.spark.rdd.RDD[(String, Int)] = MapPartitionsRDD[1143] at map at :41// 输出结果scala> println(triCountByUsername.collect().mkString("\n"))​(justinbieber,0)(matei_zaharia,1)(ladygaga,0)(BarackObama,0)(jeresig,1)(odersky,1)

    至此Spark GraphX图计算讲解完成，Spark大数据分布式处理实战笔记也到此结束。希望通过本系列可以使得作者的实操能力得到增强，也希望读者能够通过此系列入门大数据处理并且get到Spark的精彩之处～

    之后可能在此基础上继续延伸，更新Spark MLlib源码解析系列。此系列将机器学习算法与分布式架构结合在一起，使得AI人工智能算法在大数据场景下发挥更大的作用。

    前文笔记请参考下面的链接：

    Spark大数据分布式处理实战笔记（一）：快速开始

    Spark大数据分布式处理实战笔记（二）：RDD、共享变量

    Spark大数据分布式处理实战笔记（三）：Spark SQL

    Spark大数据分布式处理实战笔记（四）：Spark Streaming

    Spark大数据分布式机器学习处理实战