线性回归和线性分类器

线性回归和线性分类器

---

介绍

本次实验简述了最小二乘法、最大似然估计、逻辑回归、正则化、验证和学习曲线的基本概念，搭建了基于逻辑回归的线性模型并进行正则化，通过分析 IBMD 数据集的二元分类问题和一个 XOR 问题阐述逻辑回归的优缺点。

知识点

• 回归
• 线性分类
• 逻辑回归的正则化
• 逻辑回归的优缺点
• 验证和学习曲线

---

最小二乘法

在开始学习线性模型之前，简要介绍一下线性回归，首先指定一个模型将因变量 $y$ 和特征联系起来，对线性模型而言，依赖函数的形式如下：

y=w0+∑i=1mwixiy = w_0 + \sum_{i=1}^m w_i x_iy=w0​+i=1∑m​wi​xi​

如果为每项观测加上一个虚维度 x0=1x_0 = 1x0​=1（比如偏置），那么就可以把 w0w_0w0​ 整合进求和项中，改写为一个略微紧凑的形式：

y=∑i=0mwixi=wTxy = \sum_{i=0}^m w_i x_i = \textbf{w}^\text{T} \textbf{x}y=i=0∑m​wi​xi​=wTx

如果有一个特征观测矩阵，其中矩阵的行是数据集中的观测，那么需要在左边加上一列。由此，线性模型可以定义为：

$$\text{y}=\text{X}\text{w}+ϵ$$

其中：

• y∈Rn\textbf y \in \mathbb{R}^ny∈Rn：因变量（目标变量）。
• $w$：模型的参数向量（在机器学习中，这些参数经常被称为权重）。
• $\text{X}$：观测及其特征矩阵，大小为 n 行、m+1 列（包括左侧的虚列），其秩的大小为 $\text{rank}\left(\text{X}\right)=m+1$。
• $ϵ$：一个变量，用来表示随机、不可预测模型的错误。

上述表达式亦可这样写：

yi=∑j=0mwjXij+ϵi y_i = \sum_{j=0}^m w_j X_{ij} + \epsilon_iyi​=j=0∑m​wj​Xij​+ϵi​

模型具有如下限制（否则它就不是线性回归了）：

• 随机误差的期望为零：∀i:E[ϵi]=0\forall i: \mathbb{E}\left[\epsilon_i\right] = 0 ∀i:E[ϵi​]=0;
• 随机误差具有相同的有限方差，这一性质称为等分散性：∀i:Var(ϵi)=σ2<∞\forall i: \text{Var}\left(\epsilon_i\right) = \sigma^2 < \infty ∀i:Var(ϵi​)=σ2<∞;
• 随机误差不相关：∀i≠j:Cov(ϵi,ϵj)=0\forall i \neq j: \text{Cov}\left(\epsilon_i, \epsilon_j\right) = 0 ∀i​=j:Cov(ϵi​,ϵj​)=0.

权重 wiw_iwi​ 的估计 w^i\widehat{w}_iw i​ 满足如下条件时，称其为线性：

\widehat{w}i = \omega{1i}y_1 + \omega_{2i}y_2 + \cdots + \omega_{ni}y_n

其中对于 $\forall k$，ωki\omega_{ki}ωki​ 仅依赖于 $X$ 中的样本。由于寻求最佳权重的解是一个线性估计，这一模型被称为线性回归。

再引入一项定义：当期望值等于估计参数的真实值时，权重估计被称为无偏（unbiased）：

E[w^i]=wi \mathbb{E}\left[\widehat{w}_i\right] = w_iE[w i​]=wi​

计算这些权重的方法之一是普通最小二乘法（OLS）。OLS 可以最小化因变量实际值和模型给出的预测值之间的均方误差：

$$ \begin{array}{rcl}\mathcal{L}\left(\textbf X, \textbf{y}, \textbf{w} \right) &=& \frac{1}{2n} \sum_{i=1}^n \left(y_i - \textbf{w}^\text{T} \textbf{x}_i\right)^2 \ &=& \frac{1}{2n} \left| \textbf{y} - \textbf X \textbf{w} \right|_2^2 \ &=& \frac{1}{2n} \left(\textbf{y} - \textbf X \textbf{w}\right)^\text{T} \left(\textbf{y} - \textbf X \textbf{w}\right) \end{array}$$

为了解决这一优化问题，需要计算模型参数的导数。将导数设为零，然后求解关于 $\text{w}$ 的等式，倘若不熟悉矩阵求导，可以参考下面的 4 个式子：

∂∂XXTA=A\begin{array}{rcl} \frac{\partial}{\partial \textbf{X}} \textbf{X}^{\text{T}} \textbf{A} &=& \textbf{A} \end{array}∂X∂​XTA​=​A​

∂∂XXTAX=(A+AT)X\begin{array}{rcl} \frac{\partial}{\partial \textbf{X}} \textbf{X}^{\text{T}} \textbf{A} \textbf{X} &=& \left(\textbf{A} + \textbf{A}^{\text{T}}\right)\textbf{X} \end{array}∂X∂​XTAX​=​(A+AT)X​

∂∂AXTAy=XTy\begin{array}{rcl}\frac{\partial}{\partial \textbf{A}} \textbf{X}^{\text{T}} \textbf{A} \textbf{y} &=& \textbf{X}^{\text{T}} \textbf{y} \end{array}∂A∂​XTAy​=​XTy​

∂∂XA−1=−A−1∂A∂XA−1\begin{array}{rcl} \frac{\partial}{\partial \textbf{X}} \textbf{A}^{-1} &=& -\textbf{A}^{-1} \frac{\partial \textbf{A}}{\partial \textbf{X}} \textbf{A}^{-1} \end{array}∂X∂​A−1​=​−A−1∂X∂A​A−1​

现在开始计算模型参数的导数：

$$ \begin{array}{rcl} \frac{\partial \mathcal{L}}{\partial \textbf{w}} &=& \frac{\partial}{\partial \textbf{w}} \frac{1}{2n} \left( \textbf{y}^{\text{T}} \textbf{y} -2\textbf{y}^{\text{T}} \textbf{X} \textbf{w} + \textbf{w}^{\text{T}} \textbf{X}^{\text{T}} \textbf{X} \textbf{w}\right) \ &=& \frac{1}{2n} \left(-2 \textbf{X}^{\text{T}} \textbf{y} + 2\textbf{X}^{\text{T}} \textbf{X} \textbf{w}\right) \end{array}$$

$$ \begin{array}{rcl} \frac{\partial \mathcal{L}}{\partial \textbf{w}} = 0 &\Leftrightarrow& \frac{1}{2n} \left(-2 \textbf{X}^{\text{T}} \textbf{y} + 2\textbf{X}^{\text{T}} \textbf{X} \textbf{w}\right) = 0 \ &\Leftrightarrow& -\textbf{X}^{\text{T}} \textbf{y} + \textbf{X}^{\text{T}} \textbf{X} \textbf{w} = 0 \ &\Leftrightarrow& \textbf{X}^{\text{T}} \textbf{X} \textbf{w} = \textbf{X}^{\text{T}} \textbf{y} \ &\Leftrightarrow& \textbf{w} = \left(\textbf{X}^{\text{T}} \textbf{X}\right)^{-1} \textbf{X}^{\text{T}} \textbf{y} \end{array}$$

基于上述的定义和条件，可以说，根据高斯-马尔可夫定理，模型参数的 OLS 估计是所有线性无偏估计中最优的，即通过 OLS 估计可以获得最低的方差。

有人可能会问，为何选择最小化均方误差而不是其他指标？因为若不选择最小化均方误差，那么就不满足高斯-马尔可夫定理的条件，得到的估计将不再是最佳的线性无偏估计。

最大似然估计是解决线性回归问题一种常用方法，下面介绍它的概念。

最大似然估计

首先举一个简单的例子，我们想做一个试验判定人们是否记得简单的甲醇化学式 CH3OHCH_3OHCH3​OH。首先调查了 400 人，发现只有 117 个人记得甲醇的化学式。那么，直接将 117400≈29\frac{117}{400} \approx 29%400117​≈29 作为估计下一个受访者知道甲醇化学式的概率是较为合理的。这个直观的估计就是一个最大似然估计。为什么会这么估计呢？回忆下伯努利分布的定义：如果一个随机变量只有两个值（1 和 0，相应的概率为 $\theta$ 和 $1-\theta$），那么该随机变量满足伯努利分布，遵循以下概率分布函数：

$$ p\left(\theta, x\right) = \theta^x \left(1 - \theta\right)^\left(1 - x\right), x \in \left{0, 1\right}$$

这一分布正是我们所需要的，分布参数 $\theta$ 就是「某个人知道甲醇化学式」的概率估计。在 400 个独立试验中，试验的结果记为 x=(x1,x2,…,x400)\textbf{x} = \left(x_1, x_2, \ldots, x_{400}\right)x=(x1​,x2​,…,x400​)。写下数据的似然，即观测的可能性，比如正好观测到 117 个随机变量 $x=1$ 和 283 个随机变量 $x=0$ 的可能性：

p(x;θ)=∏i=1400θxi(1−θ)(1−xi)=θ117(1−θ)283 p(\textbf{x}; \theta) = \prod_{i=1}^{400} \theta^{x_i} \left(1 - \theta\right)^{\left(1 - x_i\right)} = \theta^{117} \left(1 - \theta\right)^{283}p(x;θ)=i=1∏400​θxi​(1−θ)(1−xi​)=θ117(1−θ)283

接着，将最大化这一 $\theta$ 的表达式。一般而言，为了简化计算，并不最大化似然 $p(\text{x};\theta )$，转而最大化其对数（这种变换不影响最终答案）：

log⁡p(x;θ)=log⁡∏i=1400θxi(1−θ)(1−xi)= \log p(\textbf{x}; \theta) = \log \prod_{i=1}^{400} \theta^{x_i} \left(1 - \theta\right)^{\left(1 - x_i\right)} = logp(x;θ)=logi=1∏400​θxi​(1−θ)(1−xi​)=

=log⁡θ117(1−θ)283=117log⁡θ+283log⁡(1−θ) = \log \theta^{117} \left(1 - \theta\right)^{283} = 117 \log \theta + 283 \log \left(1 - \theta\right)=logθ117(1−θ)283=117logθ+283log(1−θ)

为了找到最大化上式的 $\theta$ 值，将上式对 $\theta$ 求导，并令其为零，求解所得等式：

∂log⁡p(x;θ)∂θ=∂∂θ(117log⁡θ+283log⁡(1−θ))=117θ−2831−θ; \frac{\partial \log p(\textbf{x}; \theta)}{\partial \theta} = \frac{\partial}{\partial \theta} \left(117 \log \theta + 283 \log \left(1 - \theta\right)\right) = \frac{117}{\theta} - \frac{283}{1 - \theta};∂θ∂logp(x;θ)​=∂θ∂​(117logθ+283log(1−θ))=θ117​−1−θ283​;

由上可知，我们的直观估计正好是最大似然估计。现在将这一推理过程应用到线性回归问题上，尝试找出均方误差背后的道理。为此，需要从概率论的角度来看线性回归。我们的模型和之前是一样的：

$$\text{y}=\text{X}\text{w}+ϵ$$

不过，现在假定随机误差符合均值为零的 正态分布：

ϵi∼N(0,σ2) \epsilon_i \sim \mathcal{N}\left(0, \sigma^2\right)ϵi​∼N(0,σ2)

据此改写模型：

$$ \begin{array}{rcl} y_i &=& \sum_{j=1}^m w_j X_{ij} + \epsilon_i \ &\sim& \sum_{j=1}^m w_j X_{ij} + \mathcal{N}\left(0, \sigma^2\right) \ p\left(y_i \mid \textbf X; \textbf{w}\right) &=& \mathcal{N}\left(\sum_{j=1}^m w_j X_{ij}, \sigma^2\right) \end{array}$$

由于样本是独立抽取的（误差不相关是高斯-马尔可夫定理的条件之一），数据的似然看起来会是密度函数 p(yi)p\left(y_i\right)p(yi​) 的积。转化为对数形式：

$$ \begin{array}{rcl} \log p\left(\textbf{y}\mid \textbf X; \textbf{w}\right) &=& \log \prod_{i=1}^n \mathcal{N}\left(\sum_{j=1}^m w_j X_{ij}, \sigma^2\right) \ &=& \sum_{i=1}^n \log \mathcal{N}\left(\sum_{j=1}^m w_j X_{ij}, \sigma^2\right) \ &=& -\frac{n}{2}\log 2\pi\sigma^2 -\frac{1}{2\sigma^2} \sum_{i=1}^n \left(y_i - \textbf{w}^\text{T} \textbf{x}_i\right)^2 \end{array}$$

想要找到最大似然假设，即需要最大化表达式 $p\left(\text{y}\mid \text{X};\text{w}\right)$ 以得到 wML\textbf{w}_{\text{ML}}wML​，这和最大化其对数是一回事。注意，当针对某个参数最大化函数时，可以丢弃所有不依赖这一参数的变量：

\begin{array}{rcl} \textbf{w}{\text{ML}} &=& \arg \max{\textbf w} p\left(\textbf{y}\mid \textbf X; \textbf{w}\right) = \arg \max_{\textbf w} \log p\left(\textbf{y}\mid \textbf X; \textbf{w}\right)\ &=& \arg \max_{\textbf w} -\frac{n}{2}\log 2\pi\sigma^2 -\frac{1}{2\sigma^2} \sum_{i=1}^n \left(y_i - \textbf{w}^{\text{T}} \textbf{x}i\right)^2 \ &=& \arg \max{\textbf w} -\frac{1}{2\sigma^2} \sum_{i=1}^n \left(y_i - \textbf{w}^{\text{T}} \textbf{x}i\right)^2 \ &=& \arg \min{\textbf w} \mathcal{L}\left(\textbf X, \textbf{y}, \textbf{w} \right) \end{array}

所以，当测量误差服从正态（高斯）分布的情况下， 最小二乘法等价于极大似然估计。

偏置-方差分解

下面讨论线性回归预测的误差性质（可以推广到机器学习算法上），上文提到：

• 目标变量的真值 $y$ 是确定性函数 $f\left(\text{x}\right)$ 和随机误差 $ϵ$ 之和：$y=f\left(\text{x}\right)+ϵ$。
• 误差符合均值为零、方差一致的正态分布：ϵ∼N(0,σ2)\epsilon \sim \mathcal{N}\left(0, \sigma^2\right)ϵ∼N(0,σ2)。
• 目标变量的真值亦为正态分布：y∼N(f(x),σ2)y \sim \mathcal{N}\left(f\left(\textbf{x}\right), \sigma^2\right)y∼N(f(x),σ2)。
• 试图使用一个协变量线性函数逼近一个未知的确定性函数 $f\left(\text{x}\right)$，这一协变量线性函数是函数空间中估计函数 $f$ 的一点，即均值和方差的随机变量。

因此，点 $\text{x}$ 的误差可分解为：

$$ \begin{array}{rcl} \text{Err}\left(\textbf{x}\right) &=& \mathbb{E}\left[\left(y - \widehat{f}\left(\textbf{x}\right)\right)^2\right] \ &=& \mathbb{E}\left[y^2\right] + \mathbb{E}\left[\left(\widehat{f}\left(\textbf{x}\right)\right)^2\right] - 2\mathbb{E}\left[y\widehat{f}\left(\textbf{x}\right)\right] \ &=& \mathbb{E}\left[y^2\right] + \mathbb{E}\left[\widehat{f}^2\right] - 2\mathbb{E}\left[y\widehat{f}\right] \ \end{array}$$

为了简洁，省略函数的参数，分别考虑每个变量。根据公式 Var(z)=E[z2]−E[z]2\text{Var}\left(z\right) = \mathbb{E}\left[z^2\right] - \mathbb{E}\left[z\right]^2Var(z)=E[z2]−E[z]2 可以分解前两项为：

$$ \begin{array}{rcl} \mathbb{E}\left[y^2\right] &=& \text{Var}\left(y\right) + \mathbb{E}\left[y\right]^2 = \sigma^2 + f^2\ \mathbb{E}\left[\widehat{f}^2\right] &=& \text{Var}\left(\widehat{f}\right) + \mathbb{E}\left[\widehat{f}\right]^2 \ \end{array}$$

注意：

$$ \begin{array}{rcl} \text{Var}\left(y\right) &=& \mathbb{E}\left[\left(y - \mathbb{E}\left[y\right]\right)^2\right] \ &=& \mathbb{E}\left[\left(y - f\right)^2\right] \ &=& \mathbb{E}\left[\left(f + \epsilon - f\right)^2\right] \ &=& \mathbb{E}\left[\epsilon^2\right] = \sigma^2 \end{array}$$

$$\mathbb{E}[y]=\mathbb{E}[f+ϵ]=\mathbb{E}[f]+\mathbb{E}[ϵ]=f$$

接着处理和的最后一项。由于误差和目标变量相互独立，所以可以将它们分离，写为：

$$ \begin{array}{rcl} \mathbb{E}\left[y\widehat{f}\right] &=& \mathbb{E}\left[\left(f + \epsilon\right)\widehat{f}\right] \ &=& \mathbb{E}\left[f\widehat{f}\right] + \mathbb{E}\left[\epsilon\widehat{f}\right] \ &=& f\mathbb{E}\left[\widehat{f}\right] + \mathbb{E}\left[\epsilon\right] \mathbb{E}\left[\widehat{f}\right] = f\mathbb{E}\left[\widehat{f}\right] \end{array}$$

最后，将上述公式合并为：

$$ \begin{array}{rcl} \text{Err}\left(\textbf{x}\right) &=& \mathbb{E}\left[\left(y - \widehat{f}\left(\textbf{x}\right)\right)^2\right] \ &=& \sigma^2 + f^2 + \text{Var}\left(\widehat{f}\right) + \mathbb{E}\left[\widehat{f}\right]^2 - 2f\mathbb{E}\left[\widehat{f}\right] \ &=& \left(f - \mathbb{E}\left[\widehat{f}\right]\right)^2 + \text{Var}\left(\widehat{f}\right) + \sigma^2 \ &=& \text{Bias}\left(\widehat{f}\right)^2 + \text{Var}\left(\widehat{f}\right) + \sigma^2 \end{array}$$

由此，从上等式可知，任何线性模型的预测误差由三部分组成：

• 偏差（bias）: Bias(f^)\text{Bias}\left(\widehat{f}\right)Bias(f ​) 度量了学习算法的期望输出与真实结果的偏离程度, 刻画了算法的拟合能力，偏差偏高表示预测函数与真实结果差异很大。
• 方差（variance）: Var(f^)\text{Var}\left(\widehat{f}\right)Var(f ​) 代表「同样大小的不同的训练数据集训练出的模型」与「这些模型的期望输出值」之间的差异。训练集变化导致性能变化，方差偏高表示模型很不稳定。
• 不可消除的误差（irremovable error）: σ2\sigma^2σ2 刻画了当前任务任何算法所能达到的期望泛化误差的下界，即刻画了问题本身的难度。

尽管无法消除 σ2\sigma^2σ2，但我们可以影响前两项。理想情况下，希望同时消除偏差和方差（见下图中左上），但是在实践中，常常需要在偏置和不稳定（高方差）间寻找平衡。

一般而言，当模型的计算量增加时（例如，自由参数的数量增加了），估计的方差（分散程度）也会增加，但偏置会下降，这可能会导致过拟合现象。另一方面，如果模型的计算量太少（例如，自由参数过低)，这可能会导致欠拟合现象。

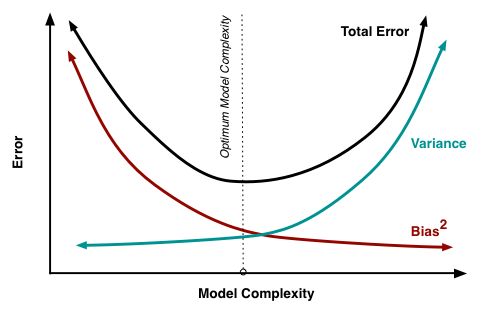
高斯-马尔可夫定理表明：在线性模型参数估计问题中，OLS 估计是最佳的线性无偏估计。这意味着，如果存在任何无偏线性模型 g，可以确信 Var(f^)≤Var(g)Var\left(\widehat{f}\right) \leq Var\left(g\right)Var(f ​)≤Var(g)。

线性回归的正则化

低偏置和低方差往往是不可兼得的，所以在一些情形下，会为了稳定性（降低模型的方差）而导致模型的偏置 Var(f^)\text{Var}\left(\widehat{f}\right)Var(f ​) 提高。高斯-马尔可夫定理成立的条件之一就是矩阵 $\text{X}$ 是满秩的，否则 OLS 的解 w=(XTX)−1XTy\textbf{w} = \left(\textbf{X}^\text{T} \textbf{X}\right)^{-1} \textbf{X}^\text{T} \textbf{y}w=(XTX)−1XTy 就不存在，因为逆矩阵 (XTX)−1\left(\textbf{X}^\text{T} \textbf{X}\right)^{-1}(XTX)−1 不存在，此时矩阵 XTX\textbf{X}^\text{T} \textbf{X}XTX 被称为奇异矩阵或退化矩阵。这类问题被称为病态问题，必须加以矫正，也就是说，矩阵 XTX\textbf{X}^\text{T} \textbf{X}XTX 需要变成非奇异矩阵（这正是这一过程叫做正则化的原因）。

我们常常能在这类数据中观察到所谓的多重共线性：两个或更多特征高度相关，也就是矩阵 $\text{X}$ 的列之间存在类似线性依赖的关系（又不完全是线性依赖）。例如，在「基于特征预测房价」这一问题中，属性「含阳台的面积」和「不含阳台的面积」会有一个接近线性依赖的关系。数学上，包含这类数据的矩阵 XTX\textbf{X}^\text{T} \textbf{X}XTX 被称为可逆矩阵，但由于多重共线性，一些本征值（特征值）会接近零。在 XTX\textbf{X}^\text{T} \textbf{X}XTX 的逆矩阵中，因为其本征值为 1λi\frac{1}{\lambda_i}λi​1​，所以有些本征值会变得特别大。本征值这种巨大的数值波动会导致模型参数估计的不稳定，即在训练数据中加入一组新的观测会导致完全不同的解。为了解决上述问题，有一种正则化的方法称为吉洪诺夫（Tikhonov）正则化，大致上是在均方误差中加上一个新变量：

L(X,y,w)=12n∣y−Xw∣22+∣Γw∣2 \begin{array}{rcl} \mathcal{L}\left(\textbf{X}, \textbf{y}, \textbf{w} \right) &=& \frac{1}{2n} \left| \textbf{y} - \textbf{X} \textbf{w} \right|_2^2 + \left| \Gamma \textbf{w}\right|^2\end{array}L(X,y,w)​=​2n1​∣y−Xw∣22​+∣Γw∣2​

吉洪诺夫矩阵常常表达为单位矩阵乘上一个系数：Γ=λ2E\Gamma = \frac{\lambda}{2} EΓ=2λ​E。在这一情形下，最小化均方误差问题变为一个 L2 正则化问题。若对新的损失函数求导，设所得函数为零，据 $\text{w}$ 重整等式，便得到了这一问题的解：

w=(XTX+λE)−1XTy \begin{array}{rcl} \textbf{w} &=& \left(\textbf{X}^{\text{T}} \textbf{X} + \lambda \textbf{E}\right)^{-1} \textbf{X}^{\text{T}} \textbf{y} \end{array}w​=​(XTX+λE)−1XTy​

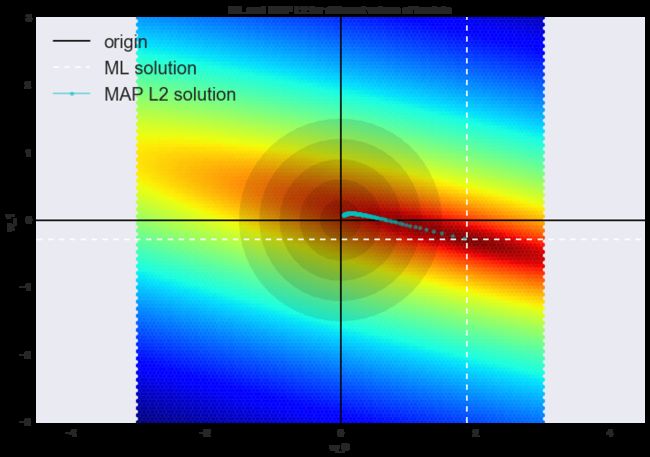
这类回归被称为岭回归（ridge regression）。岭为对角矩阵，在 XTX\textbf{X}^\text{T} \textbf{X}XTX 矩阵上加上这一对角矩阵，以确保能得到一个正则矩阵。

这样的解降低了方差，但增加了偏置，因为参数的正则向量也被最小化了，这导致解朝零移动。在下图中，OLS 解为白色虚线的交点，蓝点表示岭回归的不同解。可以看到，通过增加正则化参数 $\lambda$，使解朝零移动。

线性分类

线性分类器背后的基本思路是，目标分类的值可以被特征空间中的一个超平面分开。如果这可以无误差地达成，那么训练集被称为线性可分。

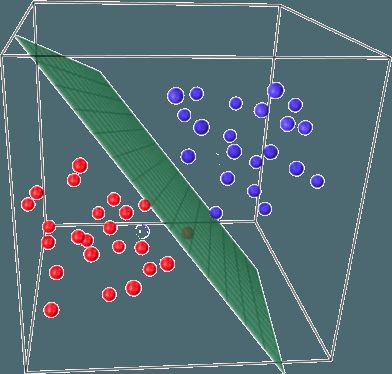
上面已经介绍了线性回归和普通最小二乘法（OLS）。现在考虑一个二元分类问题，将目标分类记为「+1」（正面样本）和「-1」（负面样本）。最简单的线性分类器可以通过回归定义：

a(x)=sign(wTx) a(\textbf{x}) = \text{sign}(\textbf{w}^\text{T}\textbf x)a(x)=sign(wTx)

其中：

• $\text{x}$ 是特征向量（包括标识）。
• $\text{w}$ 是线性模型中的权重向量（偏置为 w0w_0w0​）。
• $\text{sign}(\bullet )$ 是符号函数，返回参数的符号。
• $a(\text{x})$ 是分类 $\text{x}$ 的分类器。

基于逻辑回归的线性分类器

逻辑回归是线性分类器的一个特殊情形，但逻辑回归有一个额外的优点：它可以预测样本 $\textbf{x}\text{i}$为分类「+」的概率$p+$：

p+=P(yi=1∣xi,w) p_+ = P\left(y_i = 1 \mid \textbf{x}_\text{i}, \textbf{w}\right) p+​=P(yi​=1∣xi​,w)

逻辑回归不仅能够预测样本是「+1」还是「-1」，还能预测其分别是「+1」和「-1」的概率是多少。对于很多业务问题（比如，信用评分问题）而言，这是一个非常重要的优点。下面是一个预测贷款违约概率的例子。

银行选择一个阈值 p∗p_*p∗​ 以预测贷款违约的概率（上图中阈值为0.15），超过阈值就不批准贷款。

为了预测概率 p+∈[0,1]p_+ \in [0,1]p+​∈[0,1]，使用 OLS 构造线性预测：

b(x)=wTx∈Rb(\textbf{x}) = \textbf{w}^\text{T} \textbf{x} \in \mathbb{R}b(x)=wTx∈R

为了将所得结果转换为 [0,1] 区间内的概率，逻辑回归使用下列函数进行转换：

σ(z)=11+exp⁡−z\sigma(z) = \frac{1}{1 + \exp^{-z}}σ(z)=1+exp−z1​

使用 Matplotlib 库画出上面这个函数。

import warnings
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
%matplotlib inline
warnings.filterwarnings('ignore')

def sigma(z):
    return 1. / (1 + np.exp(-z))

xx = np.linspace(-10, 10, 1000)
plt.plot(xx, [sigma(x) for x in xx])
plt.xlabel(‘z’)
plt.ylabel(‘sigmoid(z)’)
plt.title(‘Sigmoid function’)

事件 $X$ 的概率记为 $P(X)$，则比值比 $OR(X)$ 由式 P(X)1−P(X)\frac{P(X)}{1-P(X)}1−P(X)P(X)​ 决定，比值比是某一事件是否发生的概率之比。显然，概率和比值比包含同样的信息，不过 $P(X)$ 的范围是 0 到 1，而 $OR(X)$ 的范围是 0 到 $\infty$。如果计算 $OR(X)$ 的对数，那么显然有 $\log OR(X)\in \mathbb{R}$，这在 OLS 中有用到。

让我们看看逻辑回归是如何做出预测的：

p+=P(yi=1∣xi,w)p_+ = P\left(y_i = 1 \mid \textbf{x}_\text{i}, \textbf{w}\right)p+​=P(yi​=1∣xi​,w)

现在，假设已经通过某种方式得到了权重 $\text{w}$，即模型已经训练好了，逻辑回归预测的步骤如下：

步骤一 计算：

w0+w1x1+w2x2+...=wTxw_{0}+w_{1}x_1 + w_{2}x_2 + ... = \textbf{w}^\text{T}\textbf{x}w0​+w1​x1​+w2​x2​+...=wTx

等式 wTx=0\textbf{w}^\text{T}\textbf{x} = 0wTx=0 定义了一个超空间将样本分为两类。

步骤二 计算对数比值比 OR+OR_{+}OR+​

log⁡(OR+)=wTx \log(OR_{+}) = \textbf{w}^\text{T}\textbf{x}log(OR+​)=wTx

步骤三 现在已经有了将一个样本分配到「+」分类的概率 OR+OR_{+}OR+​，可以据此计算 p+p_{+}p+​：

p+=OR+1+OR+=exp⁡wTx1+exp⁡wTx=11+exp⁡−wTx=σ(wTx) p_{+} = \frac{OR_{+}}{1 + OR_{+}} = \frac{\exp^{\textbf{w}^\text{T}\textbf{x}}}{1 + \exp^{\textbf{w}^\text{T}\textbf{x}}} = \frac{1}{1 + \exp^{-\textbf{w}^\text{T}\textbf{x}}} = \sigma(\textbf{w}^\text{T}\textbf{x})p+​=1+OR+​OR+​​=1+expwTxexpwTx​=1+exp−wTx1​=σ(wTx)

上式的右边就是 sigmoid 函数。

所以，逻辑回归预测一个样本分配为「+」分类的概率（假定已知模型的特征和权重），这一预测过程是通过对权重向量和特征向量的线性组合进行 sigmoid 变换完成的，公式如下：

p+(xi)=P(yi=1∣xi,w)=σ(wTxi). p_+(\textbf{x}_\text{i}) = P\left(y_i = 1 \mid \textbf{x}_\text{i}, \textbf{w}\right) = \sigma(\textbf{w}^\text{T}\textbf{x}_\text{i}). p+​(xi​)=P(yi​=1∣xi​,w)=σ(wTxi​).

下面介绍模型是如何被训练的，我们将再次通过最大似然估计训练模型。

最大似然估计和逻辑回归

现在，看下从最大似然估计（MLE）出发如何进行逻辑回归优化，也就是最小化逻辑损失函数。前面已经见过了将样本分配为「+」分类的逻辑回归模型：

p+(xi)=P(yi=1∣xi,w)=σ(wTxi) p_+(\textbf{x}_\text{i}) = P\left(y_i = 1 \mid \textbf{x}_\text{i}, \textbf{w}\right) = \sigma(\textbf{w}^T\textbf{x}_\text{i})p+​(xi​)=P(yi​=1∣xi​,w)=σ(wTxi​)

「-」分类相应的表达式为：

p−(xi)=P(yi=−1∣xi,w)=1−σ(wTxi)=σ(−wTxi) p_-(\textbf{x}_\text{i}) = P\left(y_i = -1 \mid \textbf{x}_\text{i}, \textbf{w}\right) = 1 - \sigma(\textbf{w}^T\textbf{x}_\text{i}) = \sigma(-\textbf{w}^T\textbf{x}_\text{i}) p−​(xi​)=P(yi​=−1∣xi​,w)=1−σ(wTxi​)=σ(−wTxi​)

这两个表达式可以组合成一个：

P(y=yi∣xi,w)=σ(yiwTxi) P\left(y = y_i \mid \textbf{x}_\text{i}, \textbf{w}\right) = \sigma(y_i\textbf{w}^T\textbf{x}_\text{i})P(y=yi​∣xi​,w)=σ(yi​wTxi​)

表达式 M(xi)=yiwTxiM(\textbf{x}_\text{i}) = y_i\textbf{w}^T\textbf{x}_\text{i}M(xi​)=yi​wTx